试论函数单调性在高中数学中的学习及应用

王世龙

(安徽省广德中学 242200)

函数单调性描述的是函数定义域与值域间的增减关系，如在给定定义域内自变量逐渐增大，函数值也随之增大，则函数为单调递增，反之为单调递减.函数单调性可解决很多函数问题，应用广泛，因此，高中数学教学中应做好函数单调性教学，不断提高学生的学习质量与效率，使学生能够灵活应用，解决各类函数问题.

一、函数单调性的学习

函数单调性不难理解，结合函数图象可知，如在定义域内非常数的连续函数没有极值点，即可称为函数是单调的，是单调递增还是递减，需要学生结合所学作进一步判断.函数学习中掌握单调性判断方法是学习的重点，具体应注重落实以下内容：

1.脚踏实地，深入理解定义

高中数学教材中给出函数单调性的定义，表述较为简单.学习中既要准确记忆，又要深入理解.尤其应注意：单调性是函数的局部性质，因此，描述函数单调性时应注意指明区间；x1，x2的取值应是任意的；判断函数单调性时除对函数值作差比较大小外，还可进行延伸，采用列表法、放缩法、作商法等.

2.注重反思，做好经验总结

除使用性质外，还可根据经验判断函数的单调性.众所周知，高中阶段学习很多函数，如二次函数、指数函数、对数函数、三角函数等.在进行这些函数学习时，应牢记函数图象，并做好单调性总结.例如f(x)为二次函数，x=x1为其图象对称轴，如图象开口向上，在(-∞,x1)上单调递减，在(x1,+∞)上单调递增.如开口向下，单调性与开口向上时相反.另外，如为复合函数时，只有内外函数单调性相同时，其才为单调递增函数，反之为单调递减函数，可简记为“同增异减”.

3.掌握公式，谨慎进行判断

判断函数单调性还可采用导数法.由于求导是判断函数单调性的基础，因此，学习中应掌握教材中给出的函数求导公式，尤其在记忆复合函数求导公式时，应将符号记忆清楚.另外，求导后找到导函数为零的点x1，如在给定区间上导函数f′(x)>0，表示函数单调递增；如为f′(x)<0，表示函数单调递减.

二、函数单调性的应用

函数单调性判断方法容易掌握，但函数问题复杂多变，要想灵活应用到解题中并非易事.因此，教学中应结合具体方法创设相关问题情境，与学生一起分析、解答，加深学生印象的同时，深化学生理解.

1.用于求解参数范围

求解参数范围的方法较多，包括分离参数、数形结合、函数单调性等方法.其中函数单调性方法应用广泛，教学中应注重优选经典例题，提高学生运用函数单调性求解参数范围的意识，掌握相关的应用技巧.

题目中给出的函数较为特殊，无法采用分离变量法求解，因此，需要借助函数单调性，找到关于a的不等式关系进行解答.

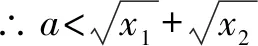
∴满足题意的a的取值范围为(-∞，2].

2.用于解答不等式

解答有关抽象函数不等式试题时，需根据函数单调性，将函数转化为定义域之间的不等关系进行求解，因此，教学中应注重讲解相关例题，使学生感受整个解题过程，掌握这一重要的不等式求解方法.

例2已知y=f(x)为定义在R上的函数，且f(0)≠0.当x>0时，f(x)>1，且对任意的a，b∈R，都有f(a+b)=f(a)·f(b)，解不等式f(x)·f(2x-x2)>1.

解答该题目时需充分利用给出的已知条件进行转化.而后求出函数值为1的自变量.最后利用函数的单调性求解.

∵对任意的a，b∈R，都有f(a+b)=f(a)·f(b),

令a=b=0，则f(0)=f(0)·f(0).

又∵f(0)≠0，则f(0)=1.

设x10，

∴f(x2)=f(x2-x1+x1)=f(x2-x1)·f(x1).

∵x2-x1>0，∴f(x2-x1)>1，

又∵f(x1)>0，∴f(x2-x1)·f(x1)>f(x1),

∴f(x2)>f(x1)，即在R上f(x)单调递增.

由f(x)·f(2x-x2)>1，可得f(3x-x2)>f(0)，

即，3x-x2>0，解得0

3.用于比较值的大小

比较函数值大小是高中数学的常见题型，难度或难或易.但多数题型需要应用函数单调性进行分析，因此，教学中可创设相关问题情境，鼓励学生积极思考，加深对单调性的理解，正确用于解答比较函数值大小试题.

例3已知函数f(x)=x2+bx+c对任意实数t都有f(2+t)=f(2-t)，那么f(1)、f(4)、f(5)的大小关系为：____.

认真观察可知函数f(x)的图象为开口向上的抛物线，要想比较f(1)、f(4)、f(5)的大小关系，需要找到其对称轴.利用函数单调性以及自变量和对称轴之间的距离进行判断.

∵对任意实数t都有f(2+t)=f(2-t)，则函数f(x)图象的对称轴为x=2.

当x>2时，函数f(x)单调递增，

∴f(5)>f(4)

因为x=1和x=4与对称轴间的距离分别为1，2，

∴f(4)>f(1).

综上可知：f(1)

4.用于分析函数极值

高中数学中分析函数极值常使用导数知识，通过判断函数的单调性求得.为使学生深入理解单调性和函数极值之间的关系，做到灵活应用，仍需通过例题加以呈现，使学生认识到函数单调性在分析函数极值中的重要作用.

例4已知Sn=2n-1+k为等比数列{an}的前n项和，求函数f(x)=x3-kx2-2x+1的极大值.

函数f(x)中带有参数k，因此，应利用给出的等比数列知识求出k值.而后运用导数通过探讨其单调性求得极值.

∵Sn=2n-1+k，则Sn-1=2n-2+k(n≥2)，两式相减得到an=2n-2(n≥2).

∵a1=S1=1+k，a2=22-2=1,a3=23-2=2,

单调性是函数的重要性质，重要性不言而喻.为使学生牢固掌握这一重要知识点，在解题中灵活应用.一方面，立足整个高中阶段，汇总判断函数单调性的方法，并为学生深入讲解，掌握不同方法的精髓以及注意事项.另一方面，做好数学题型分析，通过讲解例题，为学生做好函数单调性应用示范，鼓励学生积极思考，加深印象的同时，掌握应用技巧.