例说高考函数压轴题中的放缩策略
江苏省无锡市洛社高级中学
纵观近三年的全国卷试题,零点问题是函数压轴题中的常客,每年都考.此类问题将函数、不等式、方程等知识综合在一起,灵活多变,能有效地区分出学生在数学能力上的不同水平,故而广受命题者青睐.从知识层面看,零点存在性定理是解决这类问题必不可少的工具,而应用该定理的关键在于构造异号函数值,这是颇具技巧性的一步.标准答案常给人眼前一亮的感觉,让笔者惊叹背后蕴含的解题智慧.然而,解法固然精妙,却略显突兀,难以推广.
波利亚说过:“掌握数学就意味着学会解题”.笔者认为,解法是否自然,是教会学生解题的一个很重要的因素.基于这样的观点,经过深入的思考和实践,笔者发现并总结出解此类题的一种方法,简称为放缩.这一方法的适用范围更广,不仅能处理零点问题,在其它函数问题中也有应用,符合解题教学提倡的“注重通性通法,淡化特殊技巧”.下面通过具体问题的分析,介绍几种常用的放缩策略.
一 观察结构,代数变形
通过观察,发现式子的结构特征,与熟悉的代数公式产生联系.这种情况下,可先做一点代数上的变形,给接下来的放缩带来方便.
题目1(2018年高考全国2卷文科第21题)已知函数
(1)若a=3,求f(x)的单调区间;
(2)证明:f(x)只有一个零点.
解仅讨论第二问.

从而g(x)在(-∞,+∞)单调递增,故g(x)至多有一个零点.

思路分析先分离a,将f(x)的零点转化为g(x)的零点,便于求导讨论单调性.从g(x)的结构联想到公式通过变形再利用的有界性,这是放缩的依据.
二 分清主部,目的使然
函数表达式中,各部分对函数变化趋势的影响是不同的.决定函数变化趋势的项,笔者称之为主部,其它项则称为副部.举个例子,对于函数y=(x >0),当x→+∞时,ex是主部;当x→0时,是主部.放缩的过程就是保留主部,略去副部的过程.
题目2(2018年高考全国2卷理科第21题)已知函数
(1)若a=1,证明:当x ≥0时,f(x)≥1;
(2)若f(x)在(0,+∞)只有一个零点,求a.
解f(x)在(0,+∞)只有一个零点⇔在(0,+∞)只有一个零点.
由(1),ex > x2(x >0),从而时,当取有g(x2)>0.所以g(x)在(0,2)和(2,+∞)各有一个零点,即g(x)在(0,+∞)有两个零点.
思路分析先分离a,将f(x)的零点转化为g(x)的零点.对于函数g(x),当0< x <2时,是主部,利用ex的有界性,将ex缩小为1;当x >2时,ex是主部,结合(1)利用不等式将x2放大为
当0< x <2时,
三 借助常用不等式
指对数型函数在高考中颇为常见,下面列出几个与之相关的不等式,它们的证明非常简单,故此处略去.
(1)ex ≥x+1,当且仅当x=0时取等号.
(2)ex ≥ex,当且仅当x=1时取等号.
(3)lnx ≤x-1,当且仅当x=1时取等号.
可以发现,这几个不等式把指对数函数放缩为一次函数,这是一个飞跃.
题目3(2017年高考全国1卷理科第21题)已知函数
(1)讨论f(x)的单调性;
(2)若f(x)有两个零点,求a的取值范围.
解仅讨论第(2)问.
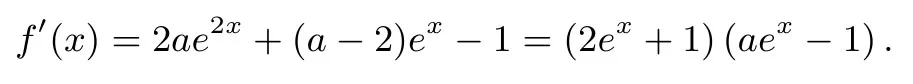
若a ≤0,则f′(x)≤0,故f(x)在(-∞,+∞)递减,与f(x)有两个零点矛盾.所以a>0.
令f′(x)=0 解得x=-lna,易知f(x)在(-∞,-lna)递减,(-lna,+∞)递增.
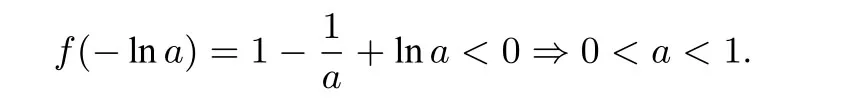
一方面,x<0时,f(x)>(a-2)ex-x>a-2-x,当x1
另一方面,f(x)=ex(aex+a-2)-x,令aex+a-2>1,即取有f(x2)>ex2-x2≥1>0.所以f(x)在(x1,-lna)和(-lna,x2)内各有一个零点,即f(x)有两个零点.综上得到0 思路分析常规方法得出0 数形结合是重要的思想方法.如果函数图象容易作出,不妨从图象入手,或许可以打开思路. 题目4(2018年高考全国3卷理科第21题)已知函数 (1)若a=0,证明:当-1< x <0时,f(x)<0; 当x>0时,f(x)>0; (2)若x=0 是f(x)的极大值点,求a. 解仅讨论第(2)问. 若a ≥0,则由(1),当x>0时有f(x)≥(2+x)ln(1+x)-2x>0,与x=0 是f(x)的极大值点矛盾,因此a<0. 设g(x)=f′(x)⇒ 设h(x)=g′(x),则 1°当x ∈(-1,0)时,h′(x)>0,h(x)在(-1,0)递增;当x ∈(0,+∞)时,h′(x)<0,h(x)在(0,+∞)递减.当x ∈(-1,+∞)时,g′(x)=h(x)≤h(0)= 0,g(x)在(-1,+∞)递减.当x ∈(-1,0)时,f′(x)=g(x)>g(0)=0,f(x)在(-1,0)递增;当x ∈(0,+∞)时,f′(x)=g(x)< g(0)= 0,f(x)在(0,+∞)递减.故x=0 是f(x)的极大值点. 2° h′(0)>0⇒- 图1 3° h′(0)<0同理,存在区间(-ε,ε),h′(x)<0.类似2°的讨论,f(x)在(-ε,ε)递减,和x=0 是f(x)的极大值点矛盾.综上,a= 思路分析通过求导至三阶,以0的情形为例,用高等数学的观点,存在0的邻域,使得h′(x)>0.问题是如何用中学数学的语言将其表述出来,仍考虑放缩.由于二次函数的图象和性质是我们非常熟悉的,因此尝试从图象角度出发,直接得到了我们想要的区间. 可以发现这四种放缩策略是一个整体,使用时往往需要综合起来.当然,放缩技巧千变万化,值得进一步去探究.笔者陈述的也仅仅是一己之见,希望与大家分享交流.四 数形结合,图象放缩