一个三角形面积公式在解析几何中的应用

广西省东兴市东兴中学

圆锥曲线是高考数学必考的一个重要知识点,主要是考查学生对圆锥曲线定义及其性质的综合运用能力,对学生运算能力的要求比较高.所以学生需要掌握一些常用的结论及变形技巧、运算技巧,以便提高运算速度.比如,多利用方程的根与系数的关系整体代换,达到“设而不求,减少计算”;涉及到共线、垂直或夹角时,利用向量解决;涉及中点与直线斜率问题,利用“点差法”等.

三角形面积问题又是圆锥曲线问题中重要的考点之一.处理三角形问题的一般步骤为:联立方程,写出根与系数的关系,然后根据题目要求使用弦长公式或点到直线的距离公式及三角形面积公式(底乘高的一半)转化成x1x2,x1+x2(或y1y2,y1+y2)的关系式,运算求得结果.而本文另辟蹊径给出了不同于传统求法的方法.这里需要用到一个与向量有关的三角形面积公式.现在先给出该三角形面积公式的推导.

定理在三角形ABC中,已知设S为三角形ABC的面积,证明:S=

证明

又因为

所以

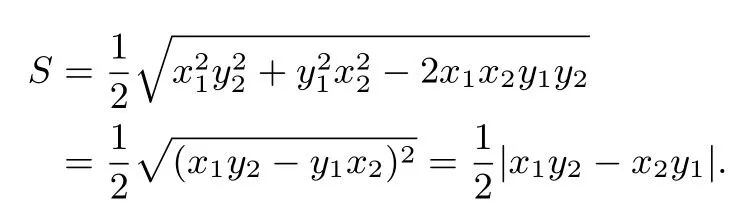
应用举例

例1已知椭圆过点且它的焦距是短轴长的倍.

(1)求椭圆C的方程.

(2)若A,B是椭圆C上的两个动点(A,B两点不关于x轴对称),O为坐标原点,OA,OB的斜率分别为k1,k2,问是否存在非零常数λ,使当k1k2=λ时,三角形OAB的面积S为定值? 若存在,求λ的值;若不存在,请说明理由.

分析对于第(2)问,由于椭圆C的参数方程为(α为参数),所以可设A(2 cosα1,sinα1),B(2 cosα2,sinα2),然后根据面积公式可得,三角形OAB面积故只需根据条件k1k2=λ,判断λ的值使得|sin(α2-α1)|为定值即可.

解(1)(略).(2)设存在非零常数λ,使当k1k2=λ时,三角形ABC的面积S为定值.因为椭圆C的参数方程为(α为参数),所以可设A(2 cosα1,sinα1),B(2 cosα2,sinα2)则由k1k2=λ得

点评按照传统的解法,本题的解法过程繁杂,需要大量的运算以及多项式的化简,同时还需要较高处理技巧.而新方法则过程简洁优美,运算量较少,没有复杂的化简过程.可以说该三角形面积公式完美的解决这一定值问题.

接下来再给出几个例子说明该三角形面积公式的实用性.

例2已知P为椭圆长轴上的一个动点,过点P的直线l与C交于点M,N两点,点M在第一象限,且若O为坐标原点,当三角形OMN的面积最大时,求点P的坐标.

分析设点P(Xp,0),类似于例1,首先由椭圆C的参数方程假设点面积公式得然后根据已知条件得到与Xp的关系,最后转化成Xp的函数求解.

解设点P(Xp,0),则-2≤Xp ≤2,因为椭圆C的参数方程为(α为参数),所以可设点

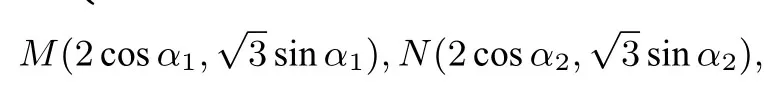
以上两式平方后相加,得10+6 cos(α2-α1)=又因为

所以由面积公式得

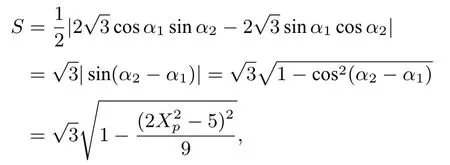
例3(2016年高考全国ⅠⅠ卷)已知椭圆的焦点在x轴上,A是E的左顶点,斜率为k(k >0)的直线交E于点A,M两点,点N在E上,MA⊥NA.求当t=4,|AM|=|AN|时,三角形AMN的面积.

分析由椭圆C的参数方程假设点

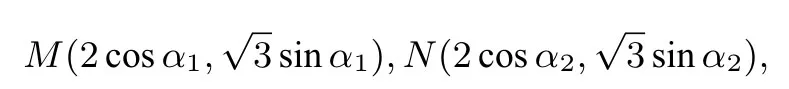
解当t=4时,椭圆E的参数方程为

A(-2,0),设点

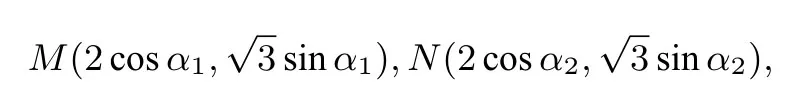
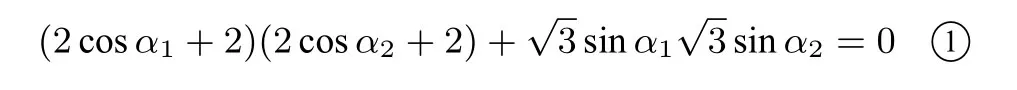
从而sinα1sinα2≤0.又因为|AM|=|AN|,所以

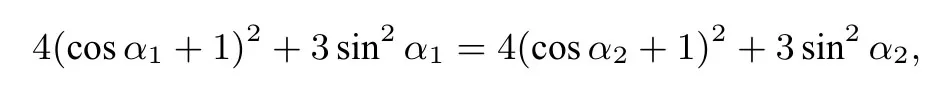
整理得,(cosα1+cosα2+8)(cosα1-cosα2)= 0.因为cosα1+cosα2+8̸=0,所以cosα1=cosα2,从而sinα1=-sinα2.结果代入,得7 cos2α1+8 cosα1+1=0,解得从而由面积公式得,三角形AMN的面积

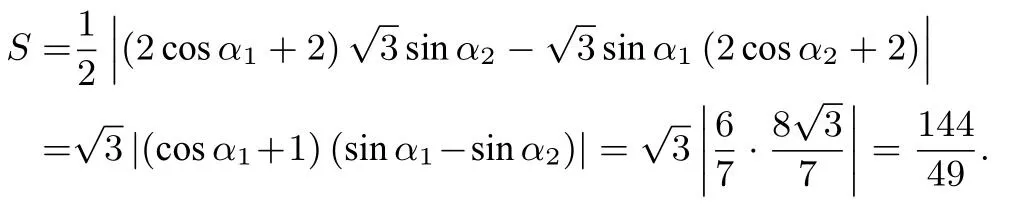
例4(2015年高考浙江卷)已知椭圆上两个不同的点A,B关于直线对称.O为坐标原点.

(1)求实数m的取值范围.

(2)求三角形AOB的面积的最大值.

分析根据椭圆参数方程(α为参数),设从而由面积公式,得再由条件两个不同的点A,B关于直线对称可得α1与α2的三角函数关系,结合该关系得到最大值.

解(1)略.

则因为A,B两点关于直线对称,又由已知易得m=0时不满足条件.所以

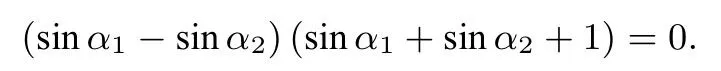
由题意,可知sinα1-sinα2̸=0,所以

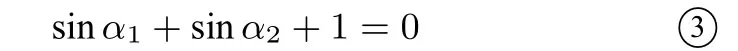
由面积公式,得三角形AOB的面积

点评以上例题都是与椭圆有关的题型.它们的传统解法都需要大量的运算以及化简,还有较高的处理技巧.而新方法确避免了这些情况.由此看出,该三角形面积公式在解决与椭圆有关的三角形面积问题时确实是可行的,并且比传统方法的运算量更小,过程步骤更固定.当然,为了能直接体现点是在椭圆上的以及直接反映点的横纵坐标的关系,解法中都利用椭圆的参数方程假设点的坐标.事实上,除了能解决与椭圆有关的三角形面积问题,该公式也可以解决与抛物线、双曲线有关的三角形面积问题的.

例5已知抛物线C:x2=2py(p >0)的焦点F,点A(x,)在C上,且点A到焦点F的距离为.

(1)求C的方程.

(2)设直线l与C交于P,Q两点,若线段PQ的中点的纵坐标为1,求三角形OPQ的面积的最大值.

分析设点P(x1,y1),Q(x2,y2)由面积公式得

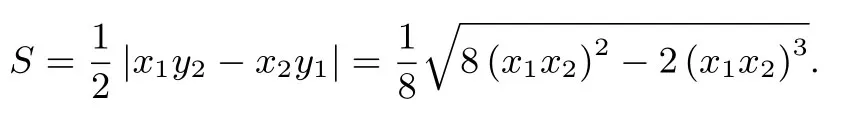
再由线段PQ的中点的纵坐标为1 讨论得x1x2的范围,从而转化成函数f(x)=8x2-2x3,-4≤x ≤4的最值问题.

解(1)F(0),准线方程为:y=因为点A到焦点F的距离为所以

故曲线C的方程为:x2=4y.

(2)设P(x1,y1),Q(x2,y2),则

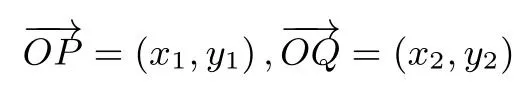
且y1+y2=2,因为所以从而-4≤x1x2≤4.由面积公式,得

令f(x)= 8x2-2x3,-4≤x ≤4,则f′(x)= 2x(8-3x),所以f′(x)= 0的解为x=[0 或x ∈[-4,0)时,f′(x)<0,f(x)单调递减;时,f′(x)>0,f(x)单调递增;时,f′(x)<0,f(x)单调递减.所以为f(x)的极大值,而所以

例6(人教版选修4-4)在平面直角坐标系xOy中,过双曲线上一点M作两条渐近线的平行线,与两渐近线的交点分别为A,B.探求平行四边形OAMB的面积,由此可以发现什么结论?

解双曲线的渐近线方程为:不妨设点M的坐标为(m,n),则直线AM的方程为:

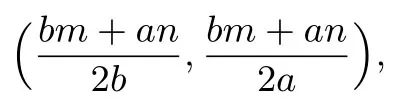
同理可得,点B的坐标为所以

由面积公式,得