对勾函数的图像为何是双曲线
安徽省合肥市第一中学
高中生大体上都知道反比例函数图像是双曲线,而且是标准形式下的等轴双曲线逆时针旋转45°而来,但是对其实轴长、焦距不甚了解.而对勾函数也是常见的,是其解析式形如:y=ax+(ab>0)的函数.教师常解释其名字来源为手绘图像酷似一对批改作业常打的“对勾”,也因像耐克商标而被称为“耐克函数”.很多师生对这种函数存在着诸多误解、迷惑和想当然的认识.比如,有的老师为了强调其与二次函数图像画法的区别,会讲:对勾函数没有对称轴,以y轴和某条递增的过原点直线为渐近线;有的学生会问:除y轴外的另一条渐近线方程是什么? 而部分教师也无从回答.本文用两种方法证明对勾函数图像也是双曲线,并探究出其实、虚半轴长和焦距、离心率和渐近线方程等结论.
1 证明
方法 1求导得如图1,设点(x0>0)为f(x)图像C上的一个点,图像C在点A处的切线为l,满足lOA⊥l.则切线l的斜率为明显y轴为图像C的一条渐近线.
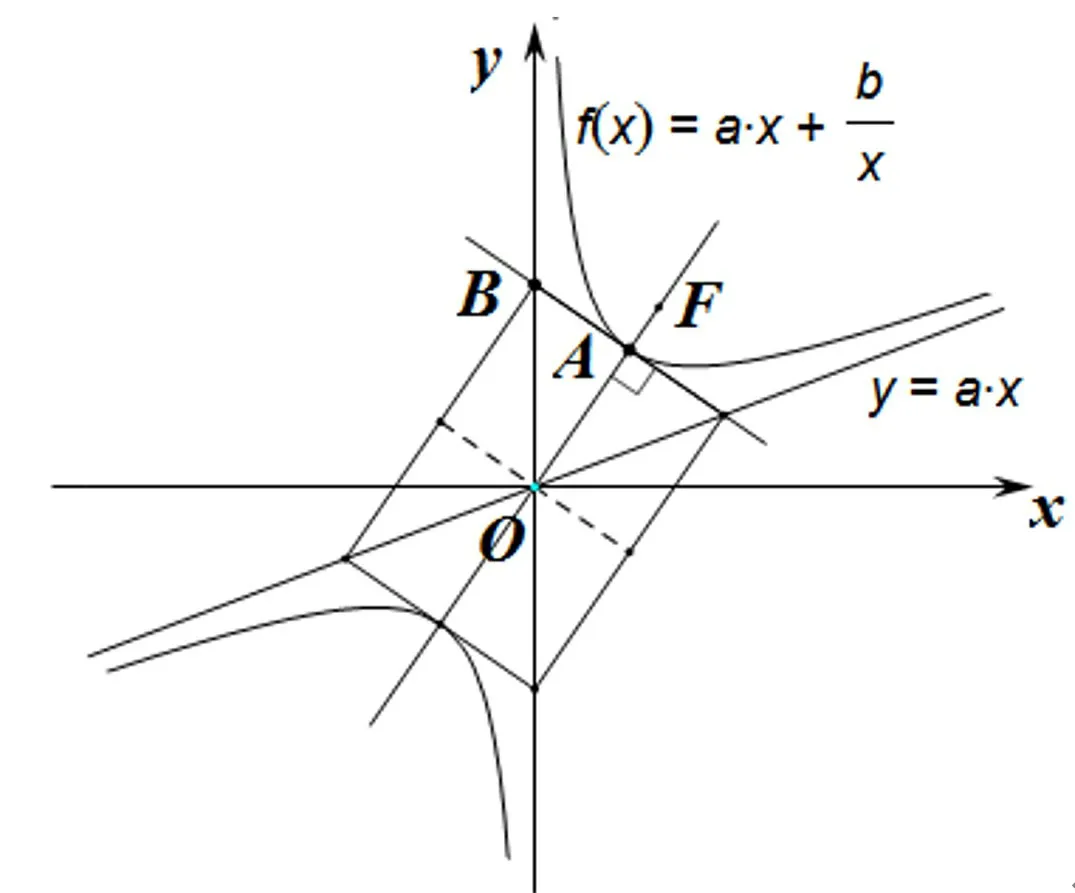
图1
由lOA⊥l,得解得故
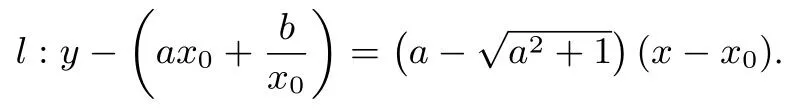
令x=0,得l与y轴交点B的纵坐标为故求得设则
另外,设点F1在射线OA上且|OF1|=c0,则故F1
设F1关于原点的对称点为F2,f(x)图像C上动点则
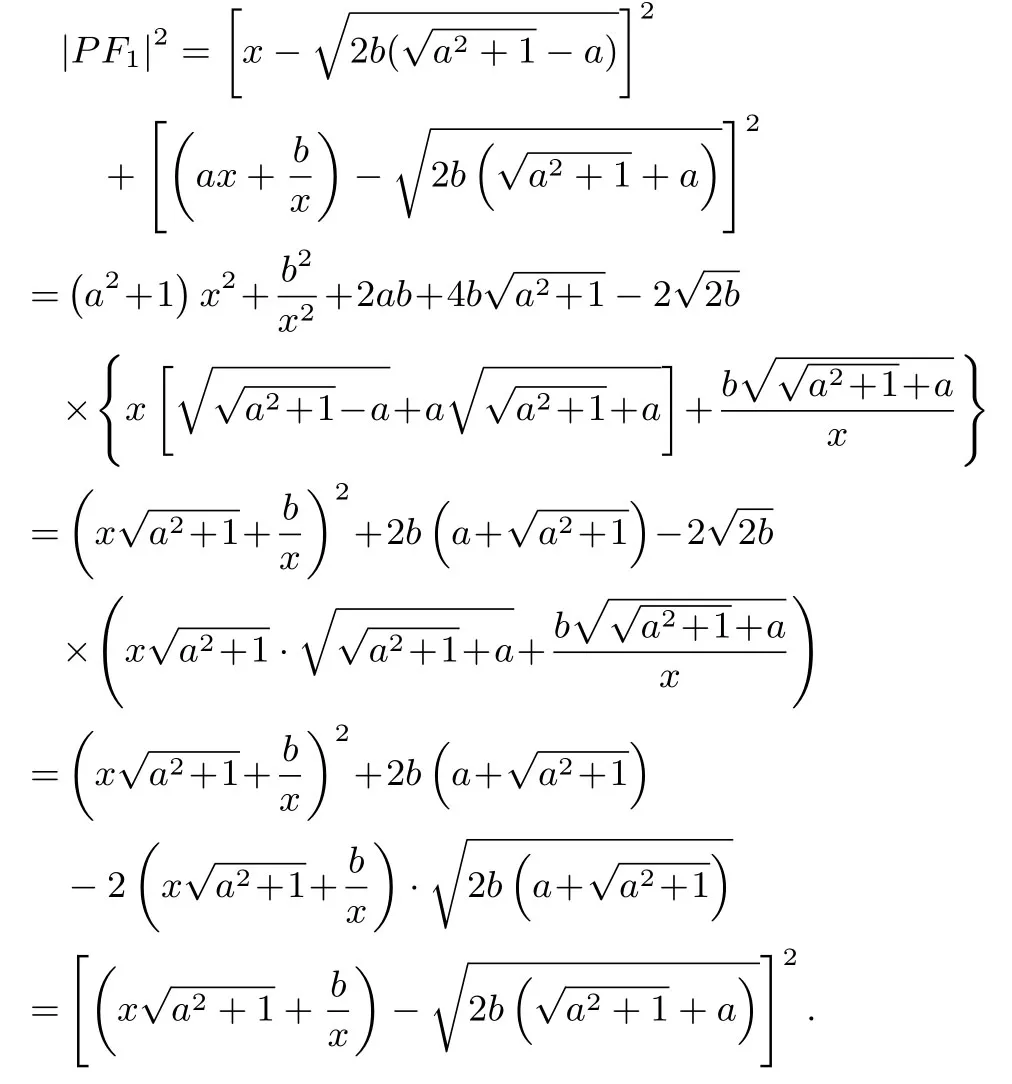
同理,
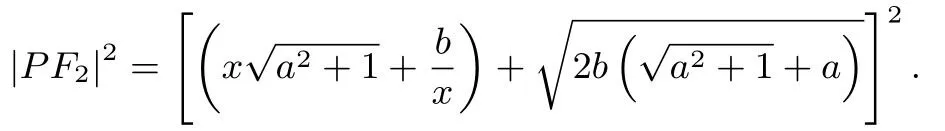
当x >0时,所以
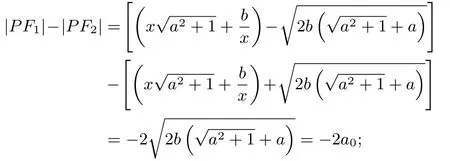
当x <0时,所以
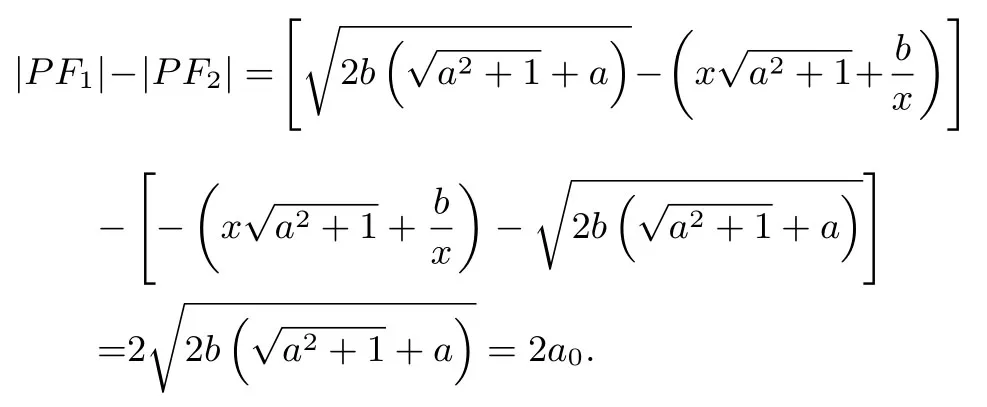
方法2设f(x)的图像C顺时针旋转后得到曲线Γ,图像C上任一点P(x0,y0)按此旋转到Q(x,y).则曲线Γ 逆时针旋转θ后得到f(x)的图像C,将逆时针旋转公式代入C得
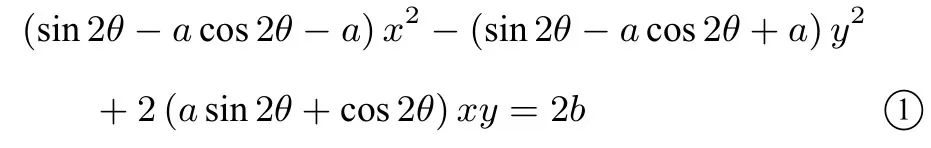
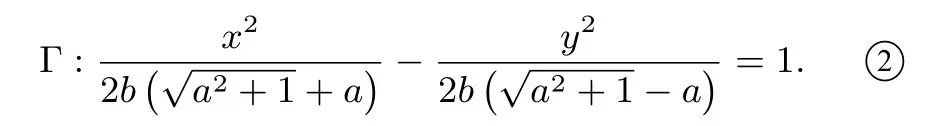
可以看出此时曲线Γ 为双曲线,从而旋转之前的f(x)=的图像C也是双曲线.
2 相关性质
2.1 推导
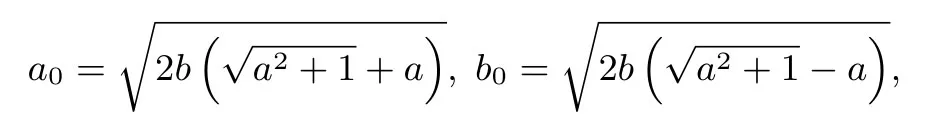
半焦距离心率而双曲线Γ的两条渐近线方程为:和x.l′1,l′2和x轴逆时针旋转θ0后,即得双曲线C的渐近线l1,l2和焦点所在对称轴l0.设l′1,l′2,l1和l2的倾斜角分别为α′1,α′2,α1和α2,则tanα′1=l0的倾斜角为θ0.
再由cos 2θ0=-asin 2θ0和得tan 2θ0=所以解得tanθ0=所以tanθ0·tanα′1=1,tanα2=tan(-α′1+θ0)故
2.2 结论
与a,b均有关的性质有:实半轴和虚半轴长分别为:
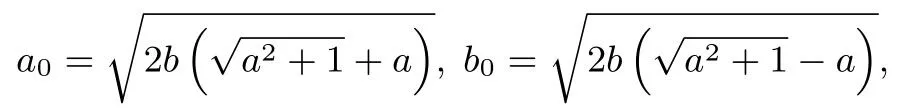
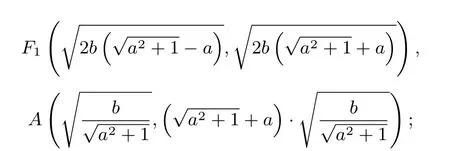
与a_有关而与_b_无关的性质有:离心率e=焦点所在对称轴为l0:y=一条渐近线为直线y=ax;
与a,b均无关的性质有:另一条渐近线恰恒为直线x=0,即y轴.
另外,用以上两种方法类似地也可以证明y=ax+在a,b<0 以及ab<0的情况下,图像也都是双曲线,并可以得到相应的相关性质结论.尤其在ab <0的情况下,其图像不再像一对“对勾”,所以可以推广为:形如y=ax+(ab ̸=0)的函数统称为“双曲线”函数.

