例谈三棱锥的外接球问题

广东省广州中学

几何体的外接球问题全国新课标卷中是一个热门考点,也是一个难点,为此也成为学生的一个薄弱点.一般情况下大都结合三棱锥考察外接球问题.怎样才能更好地解决和突破外接球问题,成为了老师和学生所渴望得到的答案.

通过大量题目的分析,发现解决三棱锥的外接球问题的方法一般有两个.第一个方法是补形,第二个方法是构造直角三角形.以下将对上述两个方法逐一进行讨论.

一 利用补形法解决三棱锥的外接球问题

《普通高中数学课程标准》中对立体几何初步的学习提出了基本要求:“在立体几何初步部分,学生将先从对空间几何体的整体观察入手,认识空间图形;再以长方体为载体,直观认识和理解空间点、线、面的位置关系;···”由此可见,长方体模型是学习立体几何的基础,掌握长方体模型,对于学生理解立体几何的有关问题起着非常重要的作用.因此长方体的外接球是学生比较熟悉的一类多面体的外接球:长方体的体对角线就是外接球的直径,长方体体对角线的中点即为外接球的球心.设长方体的长宽高分别为a、b、c,那么长方体的体对角线进而可得长方体外接球半径外接球的表面积体积也就随即可求.

例1已知S、A、B、C是球O表面上的点,SA⊥面ABC,AB⊥BC,SA=AB=1,则球O的表面积等于().

A.4πB.3πC.2πD.π

分析注意到SA⊥面ABC,BC⊥面SAB,可将此三棱锥补成长宽高分别为1,1的长方体,如图1,此时SC为长方体体对角线,可知其外接球的球心为SC中点.

把三棱锥补成一个长方体,题目也就转化为我们熟悉的题目,迎刃而解.这个方法很好,但我们会有这么两个疑问.

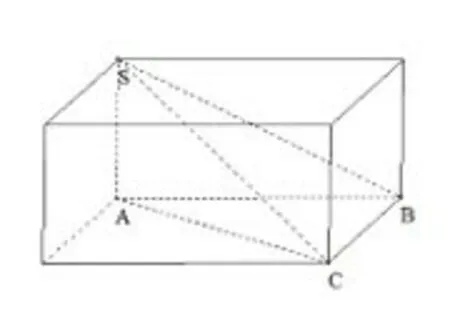
图1

第一怎么保证长方体的顶点,同时又不与三棱锥顶点重合的顶点也在球上呢?

这其实是利用了三角形的外接圆性质,还有球体的对称性,便可以证明长方体的每个顶点都会在球上.

第二是不是所有的三棱锥都能补形呢? 能补形的三棱锥有怎样的共同特征呢? 显然并不是所有的三棱锥都能补形,能补成长方体的三棱锥分为以下四类.

(1)有三个面都是直角三角形,有三条棱两两垂直,另一面为锐角三角形(如图2).这类四面体共8 个,两两垂直的三条棱就是长方体的长、宽、高.

(2)四个面都是直角三角形,有一条棱垂直于其中一个面(如图3).这类四面体共24 个,它们有一条最长棱,这条最长的棱就是长方体的体对角线.

(3)有三个面都是直角三角形,没有三条棱两两垂直,另一面为锐角三角形(如图4).这类四面体共16 个,它们有一条最长棱,这个最的棱就是长方体的体对角线.(4)四个面都是锐角三角形且对棱相等(如图5).这类四面体共2个,对棱的长度为长方体某个面对角线长.

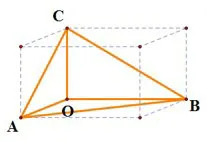
图2

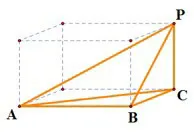
图3

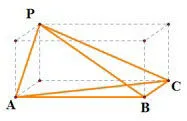
图4

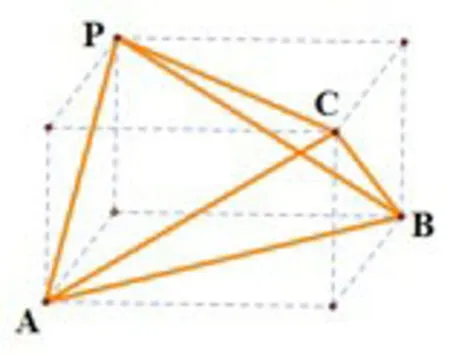
图5

练习1已知P、A、B、C是球O面上的四点,PA、PB、PC两两垂直,且PA=PB=PC=1,求球的体积与表面积.

分析PA、PB、PC两两垂直,且PA=PB=PC=1,符合正方体的特征(第一类),所以构造正方体.正方体的棱长为1,所以体对角线长为所以半径所以外接球的体积为表面积为S=4πR2=3π

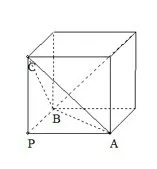
图6

练习2已知四面体ABCD满足AC=AD=BC=BD=2,则四面体ABCD的外接球的表面积为____.

分析法一:如图7,取AB、CD的中点E、F.AC=AD=BC=BD=2,知CE⊥AB,DE⊥AB,CE=DE,从而AB⊥平面CED知到A,B两点距离相等的点必在平面CED上.同理CD⊥平面AFB知到C、D两点距离相等的点必在平面AFB.因而球心O必平面CED与平面AFB的交线上.

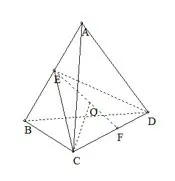
图7

又OB=OC=R.可知ΔOEB∽= ΔOCF,故球心O为EF中点.因可得从而球半径

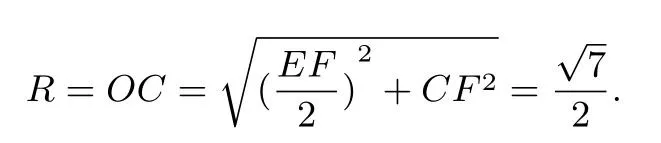
故外接球表面积S=4πR2=7π.

法二:由题发现三棱锥的对棱相等(第四类),故三棱锥可以补形成长方体.设长方体的长宽高分别为x、y、z,则

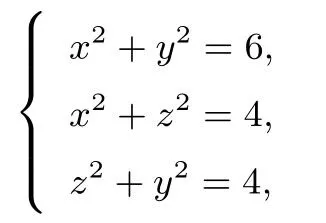
第二个题通过构造过对棱中点的截面,探索球心,给人出奇制胜的感觉,但是如果紧扣三棱锥相对棱相对这一特征,补形成长方体,这样来得更为快捷.

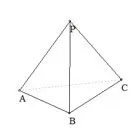
图8

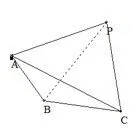
图9

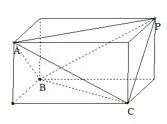
图10

二 利用构造直角三角形解决三棱锥的外接球问题

补形的方法很方便,计算量也小,但是并不是所有的三棱锥都可以补形,当这条路走不通时,我们则走第二条路—-构造直角三角形.此时引导学生类比在圆中常做的辅助线手段-垂径定理,转化到球中也可以做类似的辅助线,从而得出解决不可补形三棱锥的方法—构造直角三角形,完成知识组块的建构.让学生自然经历这两知识组块的建构,从而达到对三棱锥外接球这一问题类型的整体认识,形成清晰思路.对三棱锥外接球问题的结构化整合的思路可应用到球的其他类型的问题上,举一反三.

例2已知三棱锥P-ABC的四个顶点都在球O的球面上,若PA=AB=2,AC=1,∠BAC=120°,且PA ⊥平面ABC,则球O的表面积为().

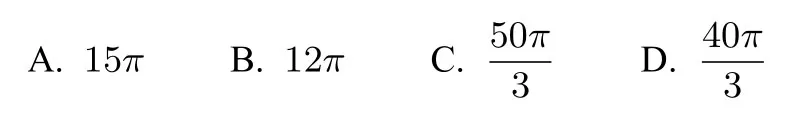
分析分析题目,该三棱锥不能补形成长方体,故另找办法.

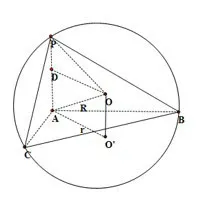
图11

设球心为O,过球心O做底面ABC的垂线,垂足为O′,连接OO′,OA,O′A.由余弦定理得为△ABC的外接圆半径r,由正弦定理得过O作OD⊥PA交PA于点D,因为OP=OA,所以D为PA中点,故OO′=AD=1.在直角三角形OO′A中,R=OA=故外接球表面积

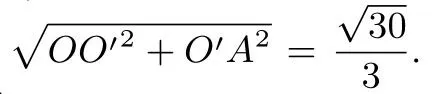
构造直角三角形,是指过球心做三棱锥某个面的垂线,垂足为三角形的外接圆圆心,外接圆半径可以由正弦定理为外接圆半径)求得,这时垂线、外接圆半径和球半径构成直角三角形,由勾股定理便可得等式.另外,还可以通过球心做垂直于面的线的垂线,这样也可以构造出跟球半径有关的直角三角形.

练习1在正三棱锥S-ABC中,侧棱SA=SB=SC=2,底面边长为1,则该三棱锥S-ABC的外接球半径是____.

分析如图12,在直角三角形AOH中,由勾股定理可得外接球半径.

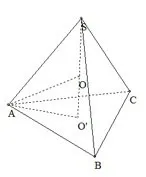
图12

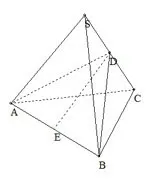
图13

练习2已知三棱锥S-ABC的所有顶点都在球面的表面上,ΔABC是边长为1的正三角形,SC为球的直径,且三棱锥S-ABC的体积为则三棱锥S-ABC的外接球的体积为____.

分析如图13,因SC为球的直径,AC=BC=1 知ΔSAB∽= ΔSBC.过点A做AD⊥SC于D,则BD⊥SC,故SC⊥平面ADB.有取AB中点E,则可得R=1,从而外接球的体积

法二过S点做三棱锥的高h,由于三棱锥体积为可得SC中点为球心O,过O点做平面ABC的垂线,垂足为O′,在直角三角形ΔOO′C中,所以从而外接球的体积

这道题第一种方法通过做与球直径垂直的截面,由三角形全等建立等式,想法巧妙,但是通过构造直角三角形,反而更为通俗易懂.

练习3矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球体积为____.

分析通过构造直角三角形的方法,可以推出球心在AC的中点处.

练习4已知在直角梯形ABCD中,AB⊥AD,CD⊥AD,AB=2AD=2CD=2,将直角梯形ABCD沿AC折叠成三棱锥D-ABC,当三棱锥D-ABC的体积最大时,其外接球体积为____.

分析通过构造直角三角形的方法,可以推出AB中点为球心.

练习3、4 虽然没有构造出具体的直角三角形,但是依然利用构造直角三角形的思路.过球心做底面直角三角形的垂线时,垂足刚好在斜边中点,同理做另一个直角三角形面的垂线时,垂足也在斜边中点处,所以最后球心只能落在棱中点处.所以本文也把这类题目归纳到构造直角三角形法中.

从上面的题目,我们发现三棱锥的外接球问题一般都是可以利用补形法或是构造直角三角形法来解决,虽然有些题目可以利用其它方法来解决,但都没显得比补形法或是构造直角三角形法来得直接与形象.从而也给学生提供了解决三棱锥外接球问题一个很清晰的思路,先看看能不能补形,不行的情况下则用构造直角三角形.这一思路可以类比到其他模型中,从而完成对外接球问题的完整认知.