对2009年高考湖北卷理科第20题的再探究

广东省佛山市罗定邦中学

1 原题再现及探究的缘起

题目(2009年高考湖北卷理科第20题)过抛物线y2=2px(p >0)的对称轴上一点A(a,0)(a >0)的直线与抛物线相交于M,N两点,自M,N向直线l:x=-a作垂线,垂足分别为M1,N1.

(1)略;(2)记ΔAMM1,ΔAM1N1,ΔANN1的面积分别为S1,S2,S3,是否存在λ,使得对任意的a >0,都有S22=λS1S3成立.若存在,求出λ的值;若不存在,说明理由.

在文[1]中,邹生书老师对上述题目进行了深入探究.邹老师先利用特殊位置,发现定值,接下来将本题所蕴含的数学背景推广至椭圆及双曲线上,并获得了如下的漂亮结论:

定理过圆锥曲线焦点所在的对称轴上任一类焦点A的直线与曲线交于M,N两点,自M,N向与点A对应的类准线作垂线,垂足分别为M1,N1,记ΔAMM1,ΔAM1N1,ΔANN1的面积分别为S1,S2,S3,则恒有S22=4S1S3成立[1].

笔者研读此文深受启发,但也提出了如下几个疑问:

(1)在文[1]中,利用点作为基本量进行求解,能否直接以弦长做为基本量求解呢?

(2)对于椭圆及双曲线而言,不含焦点的对称轴上的“类焦点”与“类准线”是否具有类似的性质呢?

(3)通过文[2],我们可知,文[1]中涉及的“类焦点”与“类准线”的实质是圆锥曲线的“极点与极线”.除了这类特殊位置外,一般的“极点与极线”还有类似的性质吗?

接下来,本文将逐步解决这些问题.

2 新的解题视角

2.1 极坐标与参数方程视角

为了说明该方法,本文先将点A及直线l特殊化.以上面的高考题为例,将点A特殊化为为焦点直线l特殊化为准线

文献[3]考虑了如下的解法.如图1,以焦点A∗为极点,x轴正半轴为极轴建立极坐标系.抛物线对应的极坐标方程为:对ΔAMM1而言,对ΔANN1而言,则有:对ΔAM1N1而言,则有观察上式即可得:成立.

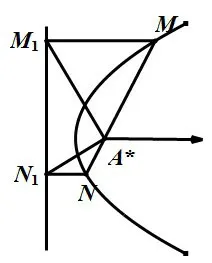
图1

图2

对于一般情况,因为没有相应的几何意义求得极坐标方程.接下来,本文运用直线的参数方程求解.

如图2,设直线MN的参数方程为:(θ为参数).与抛物线联立可得:sin2θt2-2pcosθt-2pa=0.利用韦达定理可得:

(注意t1>0,t2<0.)

对ΔAMM1而言,对ΔANN1而言,则有:

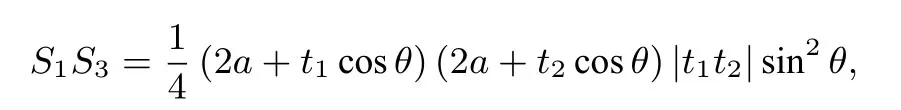
带入韦达定理得:

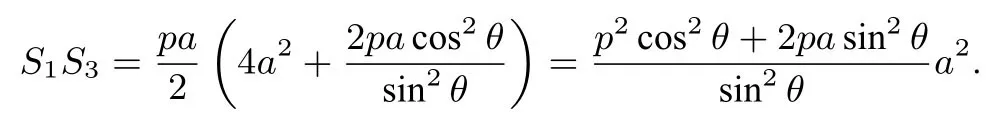
对ΔAM1N1而言,

则有

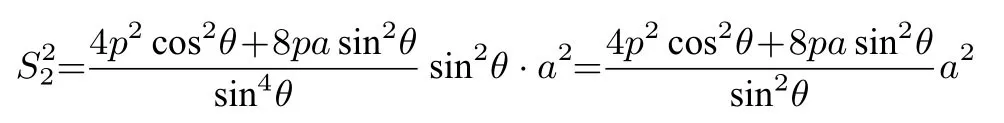
观察上式即可得:S22=4S1S3成立.

由此可知对一般的“类焦点”与“类准线”,结论也成立.

总结上面的解法可知,当点A为焦点时,本文提供的解法运算量较小,对于抛物线而言,参数方程对应的计算量也较小,当拓广至椭圆、双曲线时,运算较为繁杂,并不适合用该解法进行探究,所以本文接下来从几何的角度继续进行探究.

2.2 极点与极线视角

在文[2]中,笔者介绍了“极点”与“极线”的定义.类比至该题可知,本文的“类焦点”与“类准线”即是一对极点与极线.

极点极线的几何定义[3]:如图3,P是不在圆锥曲线上的点,过点P引两条割线依次交圆锥曲线于四点E,F,G,H,连接EH,FG交于N,连接EG,FH交于M,则直线MN为点P对应的极线.

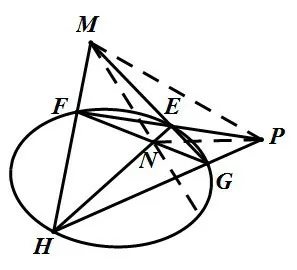
图3

定理1[4]如图4,设点P关于圆锥曲线Γ的极线为l,过点P任作一割线交Γ 于A,B,交l于Q,则

极点极线的代数定义[2]:已知圆锥曲线Γ:Ax2+Bxy+Cy2+2Dx+2Ey+F=0,则称点P(x0,y0)和直线l:D(x0+x)+E(y0+y)+F=0 是圆锥曲线Γ的一对极点和极线.其变换原则如下:在圆锥曲线中,以x0x替换x2,以替换xy,以替换x,(另一变量y也是如此.)

图4

注明极点极线的两种定义方式的本质是相同的,对于本文研究的问题而言,利用代数定义进行判断,借助几何定义进行证明.

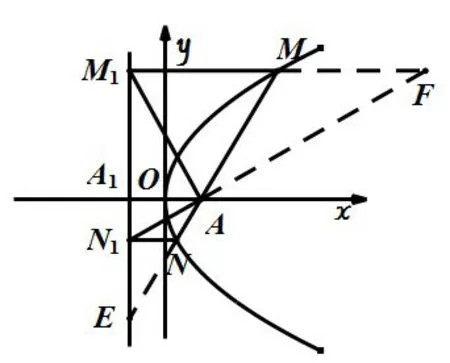
图5

根据上面的定义,点A(a,0)(a >0)与直线l:x=-a是关于抛物线的一组极点与极线,接下来,本文仅讨论直线MN斜率存在时的情况(当斜率不存在时,对应的面积比显然成立).如图5,延长MN与l交于点E,根据定理1,

易知△ENN1∽△EMM1,所以

令所以即有S3=t2S1,则有

延长N1A与M1M的延长线交于点F,易得ΔANN1∽ΔAMF,所以所以MF=MM1,即有SΔAM1F=2S1,

3 结论拓展

分析上面的两个新的解题视角,我们可将相应的性质推广至一般的圆锥曲线上.利用极坐标与参数方程的视角解决一般性问题时,涉及到参数多,运算量大.接下来,本文仅通过极点极线的视角求解.

上面的解答本身就具有一定的一般性,本文以椭圆为例,再展示一下,当极点在曲线“外部”时的情况.

如图6:设PM与l交于点E,利用定理1 可得易得:ΔENN1∽ΔEMM1,所以,

图6

令所以即有S3=t2S1,则有

延长AN1与M1M的延长线交于点F,易得ΔANN1∽ΔAMF,所以所以MF=MM1,即有SΔAM1F=2S1,所以与上式对比即可得:成立.

由此我们可以将文[1]中的结论推广如下:

定理2对于圆锥曲线C任意一组极点A/∈C和极线l,过点A的直线与曲线C交于M,N两点,自M,N向l作垂线,垂足分别为M1,N1,记ΔAMM1,ΔAM1N1,ΔANN1的面积分别为S1,S2,S3,则恒有=4S1S3成立.

4 练习

(1)已知圆C:x2+y2=9,过点A(1,2)作直线与圆C交于点M,N,自M,N向直线l:x+2y=9 作垂线,垂足分别为M1,N1.记ΔAMM1,ΔAM1N1,ΔANN1的面积分别为S1,S2,S3,是否存在λ,使得对任意的a >0,都有=λS1S3成立.若存在,求出λ的值;若不存在,说明理由.

答案存在,λ=4.提示:利用代数定义可知点A与l是圆C的一组极点与极线,根据上面的定理2,即可得答案.