数学核心素养导向下数据分析和运算能力的培养

广东省汕头市潮阳第一中学

学好高中数学,需要基础知识的积累、思想方法的掌握、联想能力的提高、运算求解能力的不断提升.其中,以运算求解能力尤为重要.

运算求解能力是思维能力和运算技能的结合.运算包括对数值的计算和近似计算,对数学表达式的变形,对几何图形相关几何量的计算求解等.运算求解能力包括分析运算条件、探究运算方向、选择运算公式、确定运算程序等一系列过程中的思维能力,也包括在实施运算过程中遇到障碍而调整运算策略的能力.

在《2017年普通高等学校招生全国统一考试大纲的说明》第160页中,提到高中数学全国卷对学生的运算能力的考查,不仅包括数的运算,还包括式的运算,兼顾对算理和逻辑推理的考查.考查是以含字母的式的运算为主,包括数字的计算、代数式和某些超越式的恒等变形、集合的计算、解方程与不等式、三角恒等变形、求导运算、概率计算、向量运算和几何图形中的计算等.运算结果具有存在性、确定性和最简性.高考中对运算求解能力的考查主要体现在运算的合理性、准确性、熟练性、简捷性.笔者经多年教学,对学生计算能力的培养积累了若干经验,总结一些主要的方法,供同行参考.

1 “独具慧眼”法

“独具慧眼”法,就是观察法,即从复杂的数据中,观察得到部分答案,再利用这部分答案推算出其余答案,从而简化运算过程,快速计算出正确的答案,起到事半功倍的作用.

例1如图1,四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1⊥平面ABCD,M为棱DD1的中点,N为棱AD的中点,Q为棱BB1的中点.

(1)证明:平面MNQ//平面C1BD;

(2)若AA1=2AB,棱A1B1上有一点P,且A1P=λA1B1(0<λ<1),使得二面角P-MN-Q的余弦值为求λ的值.

图1

简析在第二问中,以D为坐标原点,分别以线段DA,DC,DD1所在直线为x,y,z轴建立空间直角坐标系后,为方便计算,设AB=2 可得

如果将方程整理成一般的一元二次方程求解,显然计算量大.可以观察,认为左右两边分子、分母对应相等,得再去分母并两边平方得由韦达定理,类似“火中取栗”从这个方程抽取数据得

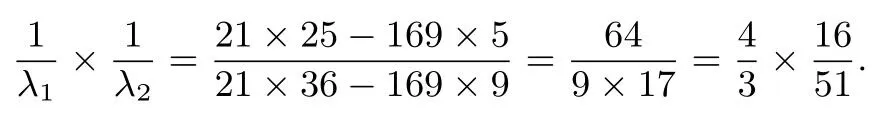
最后由0<λ<1 得

2 “欲擒故纵”法

“欲擒故纵”法,即计算数据的开始,先不进行合并、约分、开方等运算,而是先做简单的四则运算,最后才进行合并、约分、开方等运算,起到简化运算,快速得结果的作用.例如:

例2一个口袋内装有大小相同的6 个白球和4 个红球.从中任摸4 个球,求摸到白球的个数的分布列、数学期望与标准差.

简析设从中任摸4 个球,摸到白球的个数为η,则可得概率分布列为:

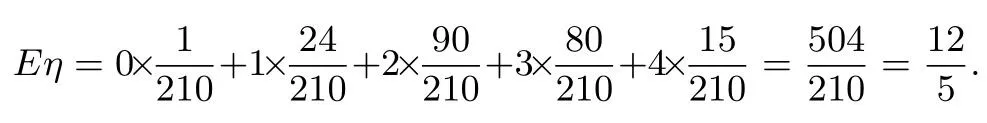
摸到白球的个数的数学期望为:

方差为:

从表格看出,如果将η=1,2,3,4 对应的概率进行约分,反而不方便.这里采取了“欲擒故纵”法,放长线钓大鱼,先列数计算,最后再约分,挺方便的.

3 “步步为营”法

“步步为营”法,即在数据较大的情况下,无法一下子观察到化简的方法,而是一点一点“蚕食”数据,经多次化简,容易得到结果.

例3某高等院校为了判断主修统计专业是否与性别有关系,“统计初步”课程的教师随机调查了选修该课的一些学生的情况,具体数据如下表:

专业性别男女合计非统计专业13 7 20统计专业10 20 30合计23 27 50

参考数据表

根据表中数据,可得到k2=4.84,由此判断选修统计专业与性别有关系的可能性达到____以上.

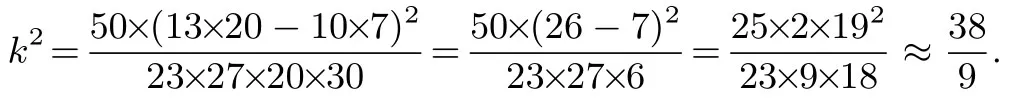
这里的第一步先套用公式,第二步的分子可以提取100与分母的100 约分,第三步将分母重新配凑,近似约分的近似值.这里用到估值计算,答案为95%.

4 “瞒天过海”法

“瞒天过海”法就是在计算过程中,利用数据或公式的特征等方法,比常规方法更简便、准确.但书写时,还是按常规方法书写.

例4已知等差数列{an}的前n项和Sn=n2+3n,则{an}的通项公式是____.

简析 利用等差数列的前n项和Sn=na1+的特征知道,Sn公式中n2前面的系数是公差的一半,an公式中n前面的系数是公差.因此,可先写出“an=2n+λ”,再结合a1=S1=4 得an=2n+2.解答题时,可以用an=Sn-Sn-1列式,但写答案时用上面方法,“瞒天过海”.

5 “金蝉脱壳”法

“金蝉脱壳”法,就是在不影响结果的情况下,舍弃“辎重”的数据,抽丝剥茧出需要计算的数据或式子,简化运算过程.

例5(2017年高考课标Ⅰ卷第21题)已知函数f(x)=

(1)讨论f(x)的单调性;

(2)若f(x)有两个零点,求a的取值范围.

解(1)f(x)的定义域为(-∞,+∞),f′(x)= 2ae2x+(a-2)ex-1=(aex-1)(2ex+1),

(i)若a ≤0,则f′(x)<0,所以f(x)在(-∞,+∞)上单调递减.

(ⅱ)若a>0,则由f′(x)=0 得x=-lna.

当x ∈(-∞,-lna)时,f′(x)<0; 当x ∈(-lna,+∞)时,f′(x)>0,所以f(x)在(-∞,-lna)上单调递减,在(-∞,+∞)上单调递增.

在第(2)问中,令f(x)= 0,分离变量a与x得换元令t=ex >0 得而f(x)有两个零点,则有两解,即直线y=a与曲线有两个交点.令则这里恒有因此,可以“金蝉脱壳”,令h(t)= 1-t-lnt,则h′(t)=注 意 到h(1)= 0,所以g(t)在(0,1)上 单调递增,在(1,+∞)上单调递减,即g(t)max=g(1)= 1.而所以当t ∈(0,1)时,g(t)∈(-∞,1); 当t ∈(1,+∞)时,g(t)∈(0,1).所以,当有两解时,a的取值范围为(0,1).