浅“移”默“画”巧成“方圆”—-全国卷中常见几何体及其外接球的数量关系问题的通性解法

广东省汕头市东厦中学

本文中将全国卷题型分为两类,分别是“三线垂直”型和“线面(面面)垂直”型,“三线垂直”型可采用“补型法”,“线面(面面)垂直”型可采用“标高法”.在解法中采用“引例说题”的形式,注重题目条件的分析,强化立体几何定理的正确使用及解题的通性通法,深化数学思想的渗透.

1 试题分析

1.1 高考真题

(1)(2019年高考全国Ⅰ卷理科第12题)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,ΔABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为().

(2)(2018年高考全国ⅠⅠⅠ卷理科第10题)设A,B,C,D是同一个半径为4的球的球面上四点,ΔABC为等边三角形且其面积为则三棱锥D-ABC体积的最大值为().

(3)(2015年高考全国ⅠⅠ卷理科第9题)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为().

A.36πB.64πC.144πD.256π

(4)(2017年全国Ⅰ卷文科第16题)已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA ⊥平面SCB,SA=AC,SB=BC,三棱锥S-ABC的体积为9,则球O的表面积为____.

(5)(2013年高考全国Ⅰ卷文科第15题)已知H是球O的直径AB上一点,AH:HB=1:2,AB ⊥平面α,H为垂足,α截球O所得截面的面积为π,则球O的表面积为____.

(6)(2017年高考全国ⅠⅠ卷文科第15题)长方体的长,宽,高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为____.

(7)(2016年高考全国ⅠⅠ文科第4题)体积为8的正方体的顶点都在同一球面上,则该球面的表面积为().

1.2 试题特征

近几年国卷的命题特点,有以下几点规律:

(1)针对的几何体主要是三棱锥、四棱锥、三棱柱、四棱柱等常见几何体;

(2)所求的外接球问题主要是体积和表面积;

(3)题目的条件中每个几何体基本都具备一个线面垂直或是面面垂直的条件.

2 必备知识

求解此类问题必备的基础知识有以下两个内容:

球的相关运算公式:S表面积=4πR2,V体积 =

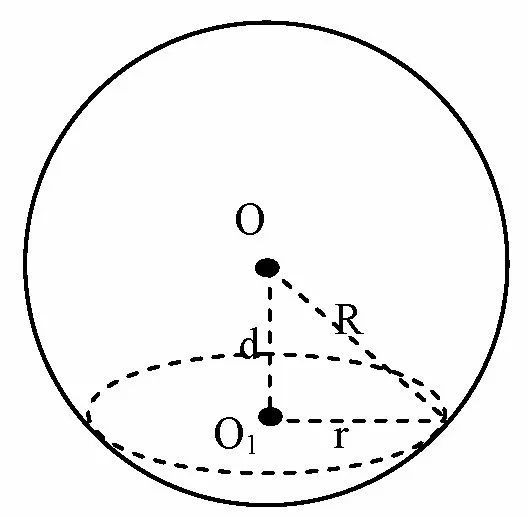
图1

球的重要性质:在球O中,球的一个截面为⊙O1,连接OO1,设OO1为d,则球的半径R,截面半径r与OO1满足R2=d2+r2.

3 例说解法

针对以上试题特征,下面将此类问题分为两种基本解法:

3.1 “三线垂直”型—-补型法

适合题目特征:几何体存在三条直线满足两两垂直的条件.

解法将几何体“补”成长方体,即是在长方体八个顶点中取其中若干个为该几何体的顶点,此时此几何体必与长方体共球,而长方体的体对角线为外接球的直径.

例1某几何体的三视图如图2,其顶点都在球O的球面上,球O的表面积是().

A.2πB.4πC.8πD.18π

图2

分析此题以三视图为条件,其直观图如图3所示,由条件可发现几何体是三棱锥,底面ABC为等腰直角三角形,有一条侧棱PA垂直底面ABC,即是有三条直线PA,AB,BC两两垂直,因此这道题可以采用“补型法”,将三棱锥“补”成长方体(如图4),即是在长方体八个顶点中取其中四个,作为此三棱锥的顶点.

图3

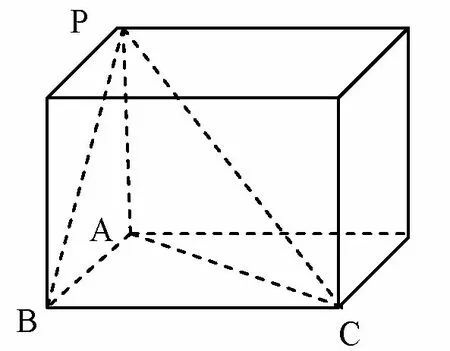
图4

解答由三视图可知:BA=BC=PA=2,则长方体体对角线PC=因此外接球半径R=球O的表面积S=4πR2=8π.

点评此法适合存在三条两两垂直的直线的几何体,如何在长方体8 个顶点中寻得对应的点作为几何体的顶点,将几何体“移”到长方体中,成了此法的关键所在.2017年高考全国ⅠⅠ卷第15题,2016年高考全国ⅠⅠ卷第4题可使用此法解答.

3.2 “线面(面面)垂直”型—-标“高”法

适合题目特征:几何体中存在一组线面垂直或面面垂直的条件根据国卷命题特点,此类题型可分为两类.

类型一如图5所示,PA垂直于底面α,垂足为A恰为底面的一个顶点.

解法由PA ⊥底面α,则将PA作为几何体的“高”,如图6所示,以三棱锥为例,则底面α必为球的一个截面O1,顶点P必为球面上一点,假设球心为O,连OO1,PO,O1A,由OO1⊥面α,可知PA//OO1,四边形OPAO1是直角梯形,OP为球O的半径R,在此类题型中,注要到PO=OA=R,因此OO1=PA,此时O1A恰为截面的外接圆半径r,利用球的基本性质OA=R,O1A=r,OO1=d,有d2+r2=R2,即可求解R.

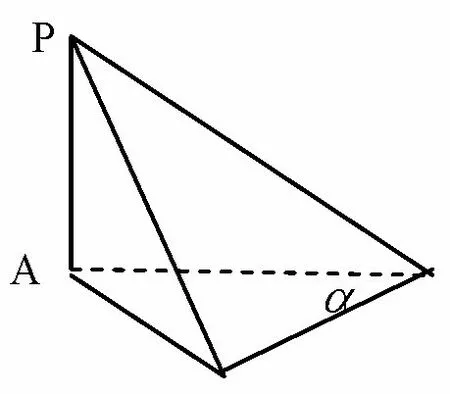
图5

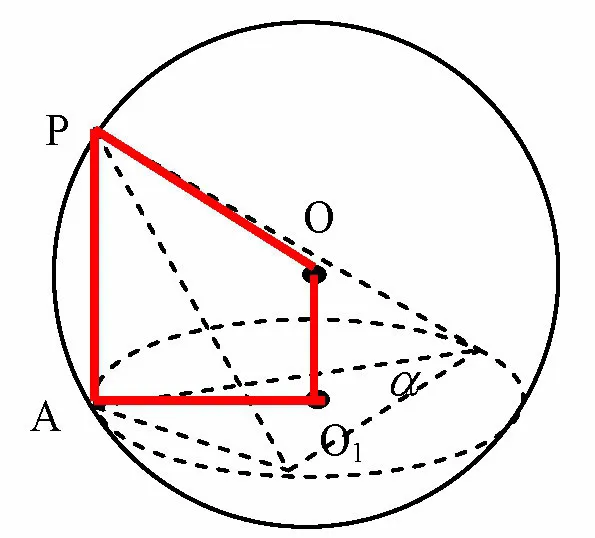
图6

例2三棱锥P-ABC中,PA ⊥平面ABC,PA=2,AB=1,∠BCA=30°,则三棱柱P-ABC的外接球的体积是____.

分析此题中PA是三棱锥的高,即是“标高”,虽然ΔABC只知道一边及一对角,只需由正弦定理求得外接圆半径r即可.

解答由题意,如图7所示,O1是底面ABC所在截面圆的圆心O为外接球球心,连OO1,OP,OA,O1A.因为OO1⊥面ABC,可知PA//OO1,OP=OA=R,所以在ΔABC中,由正弦定理可 得r=O1A=1,所以 在RtΔOO1A中,R=所以,

图7

类型二如图8所示,已知面PAB ⊥底面α,交线为AB,P点在底面的射影M在直线AB上

解法由面PAB ⊥面α,交线为AB,点P在底面的射影为M,因此PM恰为几何体“高”,如图9所示,以三棱锥为例,则底面α必为球的一个截面O1,顶点P必为球面上一点,假设球心为O,连OO1,PM,O1M,由OO1⊥面α,可知PM//OO1,四边形OPMO1是直角梯形,OP为球O的半径R.

图8

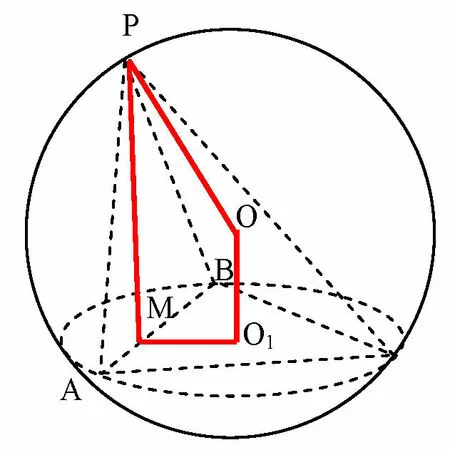
图9

在此类题型中,与类型一不同的是:此时O1M并不是截面的外接圆半径r,在直角梯形OPMO1中,设OO1=d,PM=h,OP=R,(h-d)2+O1M2=R2.只需再连O1A,OA,根据球的基本性质OA=R,O1A=r,有d2+r2=R2,根据题意求出O1M,联立两个方程组即可求解R.

例3已知四棱锥P-ABCD的顶点都在球O上,底面ABCD是矩形,平面PAD ⊥平面ABCD,ΔPAD为正三角形,AB=2AD=4,则球O的表面积为()

分析由题中的面面垂直的条件,可得到线面垂直,同时可确定顶点P在底面的射影M的位置.

解答如图10所示,由平面PAD ⊥平面ABCD,交线为AD,ΔPAD为正三角形,取AD中点M,连PM,PM ⊥AD,所以PM ⊥平面ABCD,所以AD=2,则

如图11所示,O1是底面ABC所在截面圆的圆心,O为外接球球心,连OO1,OP,PM,O1M,显然OO1//PM,在矩形ABCD中,AC是圆O1的直径,O1M=AB=2,在直角梯形OPMO1中,设OO1=d,OP=R,PM=(PM-d)2+O1M2=R2,

图10

图11

点评此法适合已知条件中有线面垂直或面面垂直的几何体,由此可确定几何体的“高”,由此确定“底面”,将几何体“移”入球中,从而构造直角梯形,利用球的基本性质,建立方程(组),求解未知量.比较两种类型的条件,除了找到几何体的“高”之外,确定顶点在底面的射影的位置成了解题的关键.在近几年的全国卷高考题中,底面基本上都是较“特殊”的三角形或四边形,只要结合图形的特征,确定该射影的位置并非难事.2013年高考文科Ⅰ卷第15题、2015年高考理科ⅠⅠ卷第9题、2017年高考文科Ⅰ卷第16题和2018年高考理科ⅠⅠⅠ卷第10题都可以使用此方法.

4 方法解读

4.1 解题方法解读

(1)“补形法”主要只针对与“长方体”共球的几何体,因此要根据几何体的特征将几何体“移”到长方体中.

4.2 思想方法解读

这种解题方法体现了两个重要的数学思想—-数形结合和转化化归,即通过巧妙作图,将立体几何的空间问题转化为平面问题,再通过代数计算解决问题.

5 链接高考

2019年高考全国Ⅰ卷理科第12题就是一道三棱锥的外接球问题,这道题作为选择题的压轴题,其考查的还是处理问题的通性通法,现将该题用上述方法解答如下:

题目(2019年高考全国Ⅰ卷理科第12题)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,ΔABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为()

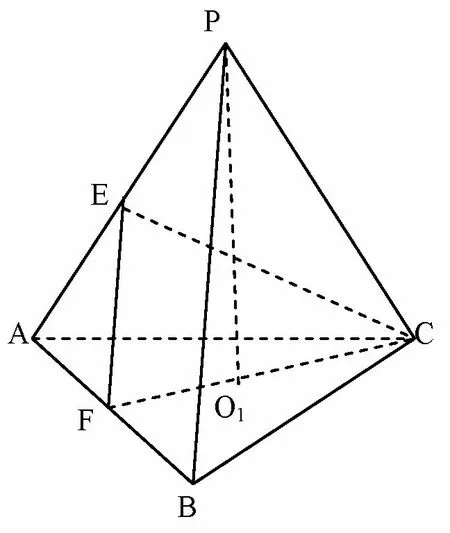
图12

图13

分析由题目条件可知此三棱锥为正三棱锥,设底面ΔABC中心为O1,则PO1为正三棱锥的高,且必过球心O,可将正三棱锥“移”入球中,如图13所示,只需利用已知条件求出正三棱锥的高,根据球的基本性质,建立方程组,即可求得球半径.

解答设ΔABC外接图圆半径为r,由已知可知设PA=2a,由E,F分别是PA,AB的中点,可得EF=a,∠CEF=90°,EF2+CE2=CF2,ΔPAC中,

由余弦定理可得

因为ΔACE中,

所以EF2+CE2=CF2可化为解得所以所以RtΔPO1C中,设PO=R,OO1=d,则

由球的基本性质可得在RtΔOO1C中,

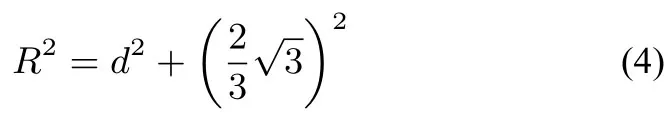
6 解题反思

一道数学题的解法不一定只有一种,一题可以多解,对于简单的空间几何体外接球的这一问题,有些题目可以适合上述两种方法.就“补形法”而言,并不一定要补成“长方体”,个别题目可以补成“三棱柱”和“六棱柱”等,形式并不唯一.本文只是针对近几年全国卷中常见的题型进行分析与归纳,就“国卷”命题特点而言,能使用“补形法”的题目,若采用“标高法”也是同样可以解答的.