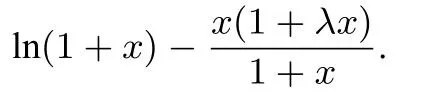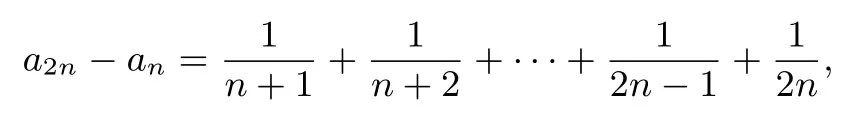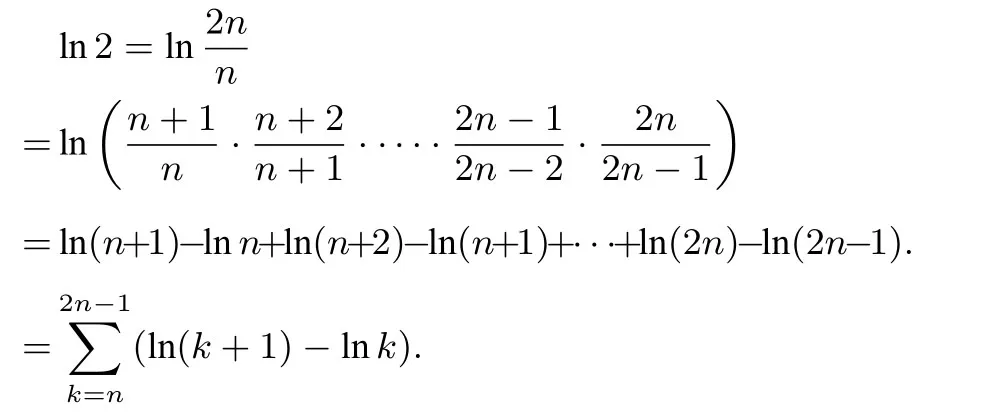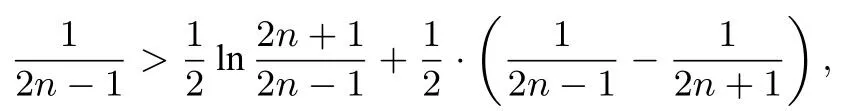探析一类不等式问题的命题思路*
福建省龙海第一中学新校区
一 前言
导数压轴试题的最后一步经常涉及到与正整数n有关的不等式证明.此类试题灵活多变,没有固定的模式套路,学生往往不知从何下手,因此成为名副其实的难点,使得众多学生“望导兴叹”.事实上,对于此类试题,如果能够透过试题表面挖掘试题深处隐含的命题规律,就能洞悉命题思路,领会命题意图,实现难点的突破和解题的高效,提高数学思维能力.
二 命题思路
此类与正整数n有关的导数压轴不等式证明试题,命题者在命制试题时,一般首先从某个不等式出发,对不等式中的x取特殊值,得到n个不等式,然后累加或者累乘,得到一个新的不等式,再对该不等式进行变形,构造,从而命制出试题.常见的不等式模型有以下几种.
模型(1)ex ≥x+1
命题思路由不等式ex ≥x+1 可知,当x >0时,x+1 对x+1分别取得 累加得 整理得 故有1n+1+2n+1+···+nn+1<(n+1)n+1. 命题分析由不等式x+1< ex出发,两边同时取n+1 次方,得到(x+1)n+1<(ex)n+1.然后对x+1分别取得到n个不等式,最后累加,再经过简单的放缩,即可得到与正整数n有关的不等式 命题1已知函数f(x)=ex-ax-1, (1)若f(x)在R 上单调递增,求a的取值范围. (2)当a >0时,设函数f(x)的最小值为g(a),求证g(a)≤0. (3)求证:对任意正整数n,都有1n+1+2n+1+3n+1+ 模型(2)ln(x+1)≤x 命题思路当x >0时,用代替x,得ln即则有nln(n+1)-nlnn<1.两边同时加上ln(n+1),得(n+1)ln(n+1)-nlnn<1+ln(n+1).所以 累加得(n+1)ln(n+1)<(1+ln 2)+(1+ln 3)+···+(1+ln(n+1)),即nln(n+1) 命题分析由不等式ln(x+1)≤x出发,用代替x得到nln(n+1)-nlnn <1,两边同时加上ln(n+1),得到(n+1)ln(n+1)-nlnn <1+ln(n+1).对n取特殊值1,2,...,n,得到n个不等式,最后累加,再两边同时消去ln(n+1),经过简单的变形,即可得到与正整数有关的不等式 命题2已知函数f(x)=ax-1-lnx, (1)若f(x)≥0 对任意的x ∈(0,+∞)恒成立,求实数a的取值范围. (2)求证:对任意的n ∈N∗,有 模型(3) 命题思路当x >0时,用代替x,得即所以1<2 ln 2,累加得 命题分析由不等式出发,用代替x得到对n取特殊值1,2,...,n,得到n个不等式,最后累加即可得到与正整数n有关的不等式 命题3已知函数f(x)=aln(x+1)+(x-1)2, (1)求f(x)的单调区间. (2)对任意n ∈N∗有 模型(4)ln(x+1)>x2-x3,x>0. 命题思路当x >0时,用代替x,得即 命题分析由不等式ln(x+1)> x2-x3(x >0)出发,用代替x,得 命题4已知函数f(x)=ax3-x2+bln(x+1),b ̸=0. (1)若a=0,b=12,求f(x)在[1,3]上的最大值. (2)若a=-,f(x)在定义域内为减函数,求实数b的取值范围. (3)是否存在最小的正整数N,使得当n ≥N时, 模型(5) 命题思路当x>0时,在不等式的两边同时除以x+1,得即所以 累乘,得 故ln((n+2)Tn)<2 ln(n+2)-(n+1)ln 2-ln(n+1). 命题分析由不等式出发,两边同时除以x+1 得到对x取特殊值1,2,...,n,得到n个不等式,最后累乘,得到最后两边同时乘以n+2,再取对数,即可得到与正整数n有关的不等式ln((n+2)Tn)<2 ln(n+2)-(n+1)ln 2-ln(n+1). 命题5已知函数f(x)=a(x+1)ln(x+1)-x2-ax(a>0)是减函数. (1)试确定a的值. 模型(6) 命题思路当x ≥1时,不等式成立.对x分别取1,2,···,n,得累加得 另一方面,当x >1时,lnx令得所以累加得 即 由(1),(2)可得ln((n+1)!·n!) 命题分析首先,由不等式出发,对x分别取1,2,···,n,得到n个不等式,累加,然后两边同时加上ln(n+1),(再经过简)单的变形,得到(1)式.其次,再由不等式出发,用代替x,得到不等式对k分别取1,2,···,n,累加后再经过变形得到(2)式.最后综合两式得到 命题6已知函数f(x)=x+lnx,g(x)=ax2-2(a-1)x+a-1. (1)求证:曲线y=f(x)与y=g(x)在(1,1)处的切线重合. (2)若f(x)≤g(x)对任意x ∈[1,+∞)恒成立,(Ⅰ)求a的取值范围.(ⅠⅠ)求证: 通过上述分析不难发现,此类导数压轴试题虽然表面复杂,看似无从入手,但是如果我们透过试题表面,逆向分析命题者命制试题的思路,就不难体会到此类试题的命制来源.在平时的教学中,教师一定要透过试题探析背后的命题思路,才能让学生深刻体会试题的来龙去脉,真正领悟到数学的思想真谛,才能促进深度学习,举一反三,触类旁通. 例题1(2013年高考全国大纲卷)已知:f(x)= (1)当x ≥0时,f(x)≤0,求λ的最小值. (2)设数列{an}的通项求证: 解析(1)略.(2)由第(1)步可知f(0)= 0,λ的最小值为.当时,f(x)<0,即ln(1+x)<由已知有 又x >0时,令得得证. 例题2(2010年高考湖北卷)已知c,a>0,的图象在点(1,f(1))处的切线方程为y=x-1. (1)用a表示出b,c. (2)若f(x)≥lnx在[1,+∞)上恒成立,求a的取值范围. 解析(1-2)略.(3)由(2)可得用n代替x得即转化成对n分别取1,2,···,n,得到n个不等式,累加,得 例题3已知函数f(x)=ax2-2xlnx-1. (1)若x=时,f(x)取极值,求f(x)的单调区间; 解析(1)略.(2)当a=1时,f(x)=x2-2xlnx-1. 易证当x >1时,f(x)>0.则当x >1时,有 上式中对n分别取1,2,···,n,得到n个不等式,累加,得 例题4已知函数f(x)=ax-2 lnx+2(1-a)+ (1)若f(x)≥0 在[1,+∞)上恒成立,求实数a的取值范围; 解析(1)略.(2)由(1)可知当a=1时,f(x)=即当x >1时,有以下解法同练习3.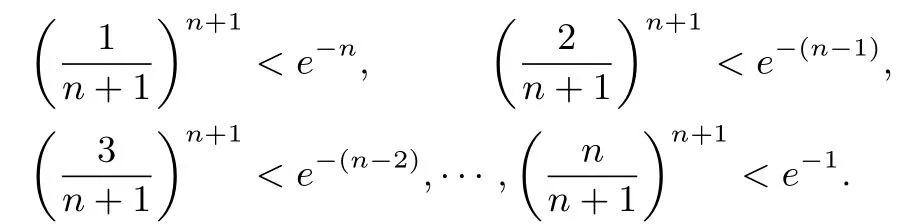
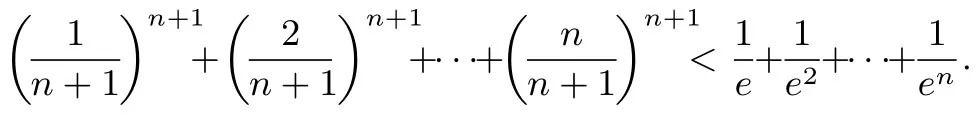
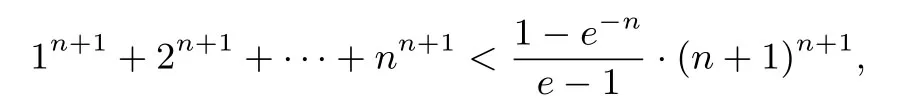
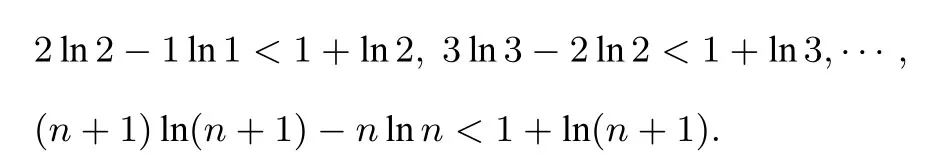
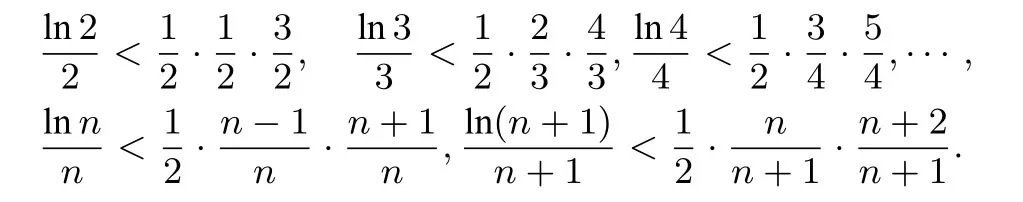
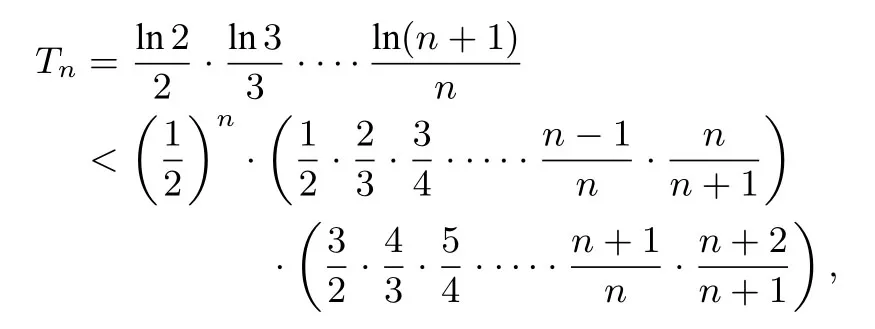
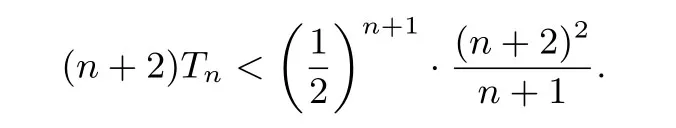
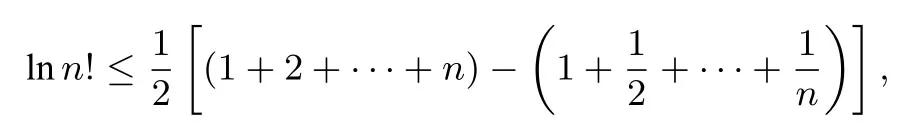
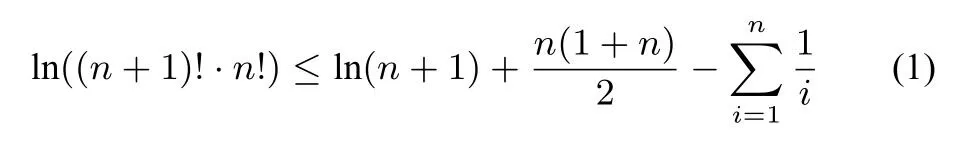
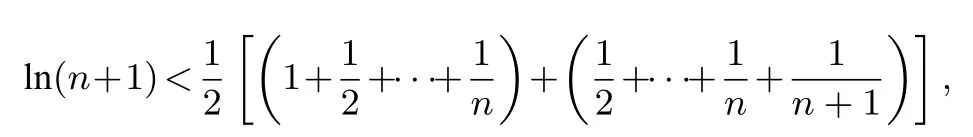
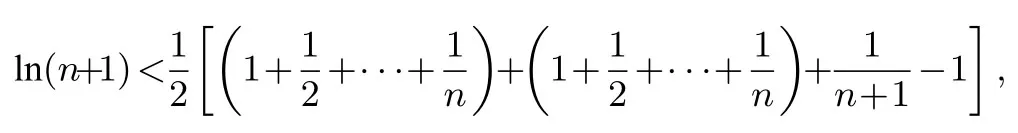
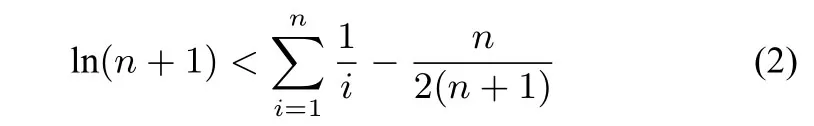
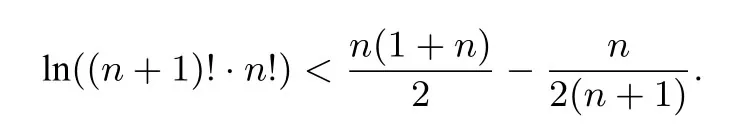
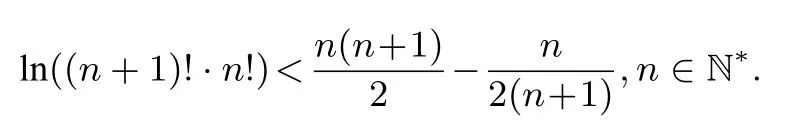
三 配套练习