2019年全国ⅠⅠ卷文科第20题的探究与推广
广东省湛江一中培才学校
广东省雷州市第八中学(524232)邓春梅
一道高考解析几何试题的命题背景可能就是圆锥曲线的一个性质定理的特殊情况.如果掌握了定理的原理,也就把握了试题的本质.对一些典型的试题,不应满足于会解,而是引导学生深入探究试题背后的知识背景,挖掘问题的本质.这样才能真正找到解决问题的方法,学会用更高观点去看待数学问题,把握问题的本质.正是《普通高中数学课程标准(2017年版)》所倡导的数学探究性课题学习,引导学生围绕某个数学问题,观察分析,自主探究,提出有意义的数学问题,探求适当的数学结论或规律.以下给出了2019年全国ⅠⅠ卷文科第20题的详细解答与分析,并深度挖掘与探究分析其性质.
一 试题展示与评析
真题(2019年高考全国ⅠⅠ卷文科第20题)已知F1,F2是椭圆C:的两个焦点,P为C上的点,O为坐标原点.
(Ⅰ)若ΔPOF2为等边三角形,求C的离心率;
(Ⅱ)如果存在点P,使得PF1⊥PF2,且ΔF1PF2的面积等于16,求b的值和a的取值范围.
解析(Ⅰ)若ΔPOF2为等边三角形,则P的坐标为(代入方程可得解得所以
(Ⅱ)由题意可得|因为PF1⊥PF2,所以所以所以4b2, 所以所以解得b=4.
评析此题主要考查椭圆的基本性质、椭圆的离心率、椭圆上点到焦点的距离(焦半径)、过焦点的弦长(焦点弦)、焦点三角形的面积、等边三角形和直角三角形及其面积的知识,考查考生运用数形结合的思想方法和综合应用数学知识解决问题的能力,体现曲线与方程、转化与化归的思想,着重考查学生逻辑推理、直观想象和数学运算等数学核心素养.本题平中见奇、内涵丰富、解法多样,是一道具有研究性学习价值的好题.
二 教材寻根
高考题的命题有些是来源于教材,但往往又高于教材,因而我们的课堂教学需要回归教材,扎根教材,根深才能叶茂,源远方能流长.2019年全国ⅠⅠ卷文科第20题来源于新课标人教B版选修2-1 第47页练A 第5题.
题目(新课标人教B版选修2-1 第47页练A 第5题)已知椭圆的两个焦点分别为F1,F2,点P在椭圆上,且∠F1PF2=60°,则△F1PF2的面积为____.
教材中的例、习题具有典型性与代表性,能有效检查学生对重点知识的掌握及灵活应用的程度.分析历年的高考试题,可以发现,很多高考试题的原型都来自于课本教材,适当地进行一些改编和创新.高考的命题指导思想中也指出,要考查学生对基础知识、基本能力的掌握程度和运用所学知识分析、解决问题的能力.因此,对教材例、习题的探究是高三备考复习的重要方式之一.
三 性质研究
3.1 正向探究
教材中的例题或习题具有典型性、代表性,对其深入探究,常可得到解决一类问题的一般结论.
结论1若F1,F2是椭圆的两个焦点,点P为椭圆C上任一点,∠F1PF2=θ,则△F1PF2的面积为S=

图1
证明由椭圆的定义,得2c.在△F1PF2中,由余弦定理得

所以(2c)2=(2a)2-2|PF1| · |PF2|(1+cosθ),所以所以S=故△F1PF2的面积为
3.2 类比探究
由椭圆联想到双曲线,则有:
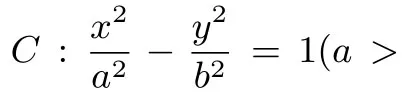
结论2若F1,F2是双曲线0,b >0)的两个焦点,点P为双曲线上任一点,∠F1PF2=θ,则△F1PF2的面积为

图2
3.3 变式探究
结论3若F1、F2是椭圆的两个焦点,点P为椭圆C上任一点,∠F1PF2=θ,则△F1PF2的面积为
证明由椭圆的定义,得2c.在F1PF2中,由余弦定理得

3.4 纵向探究
椭圆中焦点三角形与离心率范围的三个性质.
性质1若椭圆的两个焦点为F1、F2,P为其上一点,且|PF1|=λ|PF2|(λ >1),则该椭圆的离心率e的取值范围为
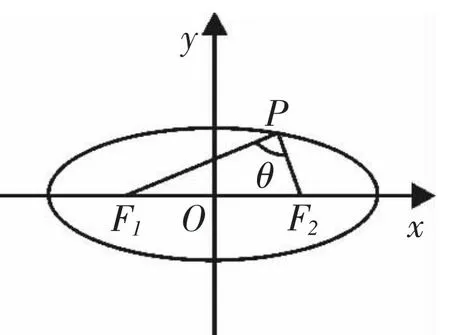
图3
证明如图3,由椭圆的定义,得|PF1|+|PF2|=2a,由解得
因为λ >1,由三角形的性质有:即解得:1.所以双曲线的离心率e的取值范围为1).
性质2若双曲线的0)两个焦点为F1、F2,P为其上一点,且|PF1|=m|PF2|(m >1),则该双曲线的离心率e的取值范围为

图4
证明因为|PF1|=m|PF2|(m>1),所以点P在双曲线的右支上,如图4由双曲线的第一定义,得2a,由解得
所以双曲线的离心率e的取值范围为
性质3若椭圆的两个焦点为F1、F2,P为其上一点,且∠F1PF2=θ,则该椭圆的离心率e的取值范围为
证明在ΔF1PF2中,由余弦定理及椭圆的定义

由以上(1)(2)(3)得

性质4若椭圆的两个焦点为F1、F2,P为其上一点,且∠PF1F2=α,∠PF2F1=β,则该椭圆的离心率
证明在ΔF1PF2中,由正弦定理得所以所以所以所以椭圆的离心率
四 真题回顾
与焦点三角形相关题型大致有六种形式,如图5所示:

图5
椭圆中与焦点三角形有关的问题是各类考试的热点,经久不衰,题型灵活多样.其解题通法是用到椭圆定义、三角形中的余弦定理、基本不等式等,融合的知识点较多,对学生来说有一定的难度.
由以上性质不难发现,历年高考题也均考查以上圆锥曲线的焦点三角形问题,体现了高考试题“常考常新,推陈出新”的理念,在解决有时,灵活运用上面的性质,不仅比较容易找到解题的突破口,而且往往会获得简洁、明快的解题方法和途径.下面略举几例说明上述性质的应用.
例1(2016年高考浙江卷理科第7题)已知椭圆与双曲线的焦点重合,e1、e2分别为C1、C2的离心率,则().

A.m>n且e1e2>1 B.m>n且e1e2<1
C.m 解设P为椭圆与双曲线在第一象限内的公共点,F1、F2为它们的公共焦点,则所以所以m>n. 设∠F1PF2=θ.由结论1、2,得所以所以即(m+n)2+(m-n)2=4c2,所以m2+n2=2c2.所以又e1̸=e2,所以所以e1e2>1.故选A. 例2(2016年全国高中数学联赛)已知F1、F2为椭圆和双曲线的公共焦点,P为它们的一个公共点,且则该椭圆和双曲线的离心率之积的最小值是(). 解设椭圆方程为双曲线方程为由结论1、2,得e2分别为C1、C2的离心率,则所以当且仅当即时等号成立.故选B. 例3(2015年高考全国Ⅰ卷理科第5题)已知M(x0,y0)是双曲线上一点,F1、F2为双曲线C的两个焦点,若则y0的取值范围是(). 解设∠F1MF2=θ,则由结论2,得 又SΔF1MF2,所以故选A. 例4 (2014年高考湖北卷理9)已知F1、F2为椭圆和双曲线的公共焦点,P为它们的一个公共点,且则该椭圆和双曲线的离心率的倒数之和的最大值是(). 解设椭圆方程为双曲线方程为 例5(2013年高考浙江卷理科第9题)已知F1、F2是椭圆与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2是矩形,则C2的离心率是(). 解由结论1,得SΔF1AF2=12·tan 450=1,由结论2,得SΔF1AF2=b2·cot 450=b2=1. 例6(20122年高考2安徽卷文科第20题)已知F1、F2分别是椭圆的左、右焦点,点A是椭圆C的顶点,点B是直线AF2与椭圆C的另一个交点,∠F2AF1=60°. (Ⅰ)求椭圆C的离心率; (ⅠⅠ)已知ΔAF1B的面积为求a,b的值. 解(Ⅰ)椭圆的离心率为(过程略).(ⅠⅠ)由结论3, 即acb2=40a2-10c2.由得代入上式得6c4=150c2,即c=5.所以 例7(2011年高考江西卷文科第20题)已知F1、F2是椭圆的两个焦点,P为椭圆上一点∠PF1F2=150,∠PF2F1=750,则椭圆C的离心率为____. 解由性质4,得 例8(2019年厦门质检)已知椭圆b >0)的两个焦点为F1、F2,M为其上一点,且则该椭圆的离心率e的[取值范围为)__[__.) 解由性质1易知,λ=3,所以椭圆的离心率e的取值范围为 例9(2019年海口一模)已知双曲线的0)两个焦点为F1、F2,P为其上一点,且|PF1|=2|PF2|,则该双曲线的离心率e的取值范围为(). A.(1,3)B.(1,3]C.(3,+∞)D.[3,+∞) 解由性质2 易知,m=3,(1,3],所以椭圆的离心率e的取值范围为(1,3],故选B. 例10(2019年青岛二模)已知椭圆的1(a > b >0)两个焦点为F1、F2,M为其上一点,且∠F1MF2=120°,则该椭圆的离心率e的取值范围为____. 解由性质3 易知,所以椭圆的离心率e的取值范围为 从以上例子我们不难发现,利用椭圆中焦点三角形的性质去解与离心率范围和面积有关的问题时,能降低思维强度,避免冗长的推理和运算,大大降低难度,使解题过程简捷明了,从而获得事半功倍的解题效果! G.波利亚有句名言:“掌握数学就是意味着善于解题,如果我们在日常的教学中,能对课本例习题作深入的研究,一题多解,一题多变,多题一法进行变式教学,立根课本,必定能取得丰硕的成果”. 在数学教学中,我们要善于挖掘教材的潜在教学功能.教材中有一些典型性题目,它们或者是重要的结论,或者体现某种数学思想方法,或者是某个一般数学命题的具体形式,它的延伸、转化和拓广,可以呈现出丰富多彩的数学内容.我们必须充分重视课本典型例题、习题的探究,这是“用教材教”之根本,也是教师专业成长的必有之路. 以上性质的总结不仅可以作为一般公式直接应用,也可解决一些难以用常规方法解决或计算太复杂的简单题,加快答题的速度,节省答题的时间,提高高考的得分率.同时通过对这些性质的探究过程可以发现,关于焦点三角形的离心率问题,若只知一个角可以借助余弦定理进行解答,而若知两个角,则常借助正弦定理.若以三角形作为研究对象,不外乎研究边与边的关系,边与角的关系,角与角的关系,周长和面积等.而周长和面积的研究,多借助圆锥曲线的第一定义和余弦定理进行处理,故掌握圆锥曲线的定义,利用定义进行解题是解决圆锥曲线题的常规解法和一般思路.

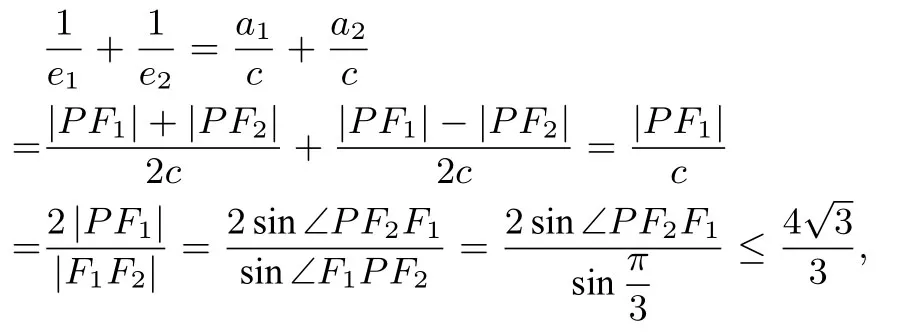



五 备考建议

