多想少算视角下2019年高考数学试题分析*

四川省内江师范学院数学与信息科学学院

高考数学命题将“多考点想,少考点算”作为一条基本命题理念.[1]基于此,衍生出了一系列优化运算的解题策略,比如:利用定义、利用模型、正难则反、数形结合、特殊化、极限策略、猜想策略、换元策略、设而不求、分离变量等等.文中以2019年高考试题为例,介绍一些实现“多想少算”的解题策略,以期读者充分感受“多想少算”的命题理念和策略的魅力.[2]

一 利用定义

李邦河院士指出:“数学是玩概念的,而不是技巧.”熟练运用定义解题,常常可获得快捷有效的解题途径.

例1(2019年高考浙江卷第8题)设三棱锥V-ABC的底面是正三角形,侧棱长均相等,P是棱V A上的点(不含端点).记直线PB与直线AC所成角为α,直线PB与平面ABC所成角为β,二面角P-AC-B的平面角为γ,则().

A.β <γ,α<γB.β <α,β <γ

C.β <α,γ <αD.α<β,γ <β

解作PD//CA交V C于D,取PD中点E,连接BE,作EH⊥平面ABC于H,连接BH,作PF⊥平面ABC于F,连接BF,作PG⊥AC于G,连接FG.

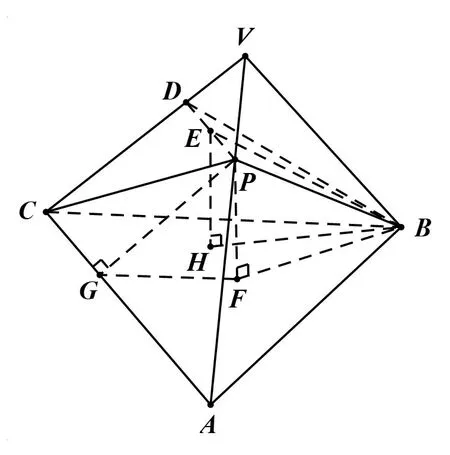
图1

易知V-ABC为正三棱锥,故PB=BD,则BE⊥PD.又PD//CA,则α=∠BPD.显然β=∠PBF,γ=∠PGF.易知

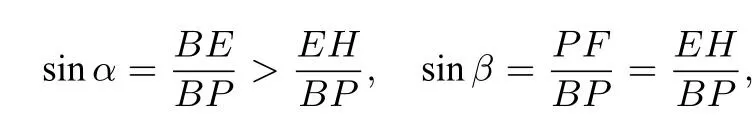
则sinα>sinβ.由得α>β.又

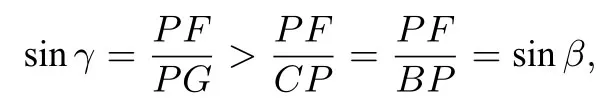
则γ >β,故α>β,γ >β.

评注解答中抓住异面直线成角、线面角、二面角定义,减轻了思维负荷,实现了问题的快速解答.

二 利用模型

数学模型是研究者依据研究目的,将所研究客观事物的过程和现象的主要特征、主要关系,采用形式化的数学语言,概括或近似地表达出来的一种结构.[3]如恒等式模型、三点共线模型、距离模型、面积模型等,利用模型解题,可缩短思考时间,提升解题效率.

例2(2019年高考天津卷理科第14题)在四边形ABCD中,AD//BC,AB=AD=5,∠A=30°,点E在线段CB的延长线上,且AE=BE,则

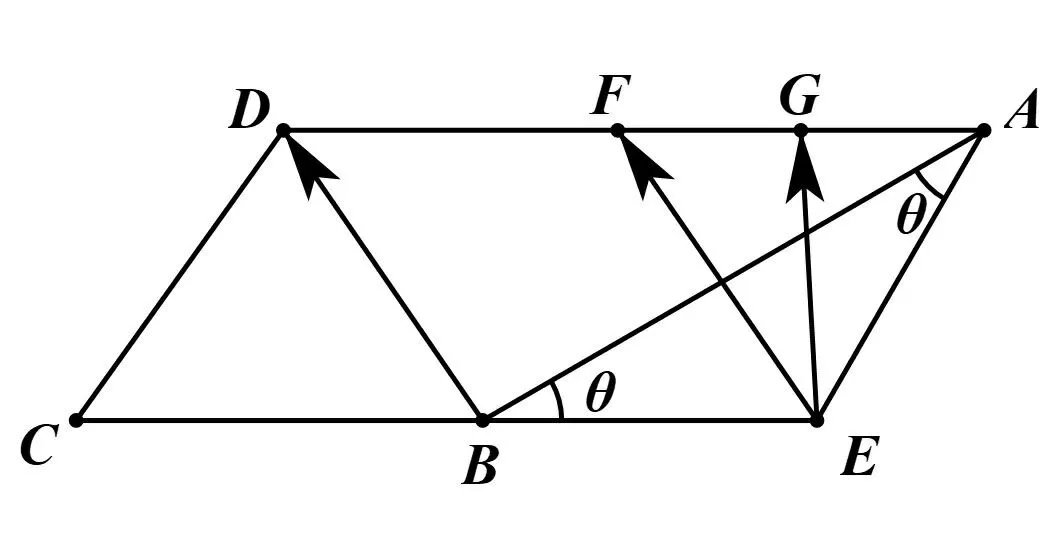
图2

解作EF//BD交AD于F,取AF中点G,连接EG.由已知得,θ=30°,则∠AEB=120°,由正弦定理得则AE=BE=DF=2,AF=又EG2=AE2+AG2-2AE·AG·cos 2θ则

评注利用向量的恒等式模型(对于任意向量有将表征为关于的关系式,再利用正弦定理求出向量的模.解答思路清晰,层层递进,优化了解题过程.

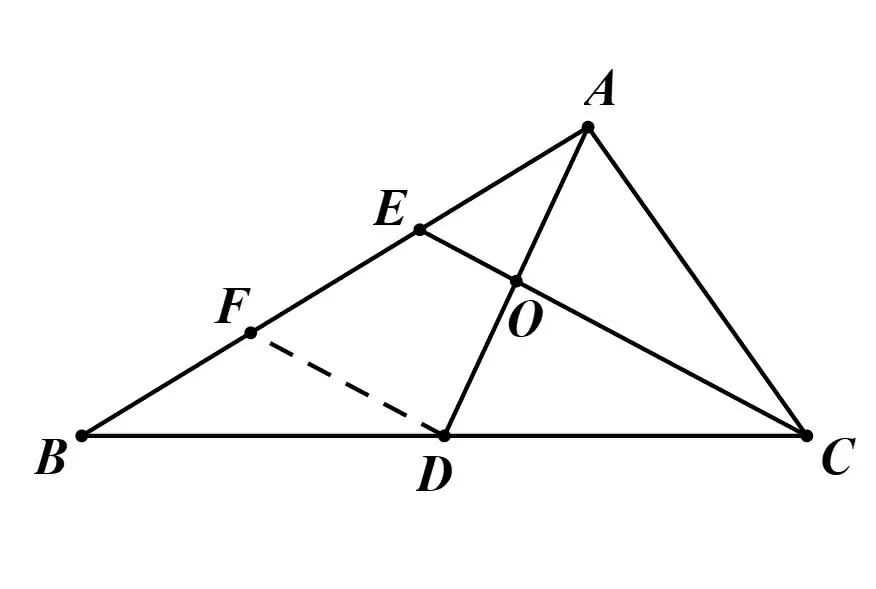
图3

例3(2019年高考江苏卷第12题)如图3,在ΔABC中,D是BC的中点,E在边AB上,BE=2EA,AD与CE交于点O.若则的值是____.

解如图,过D作DF//CE,交AB于F,由BE=2EA,D为BC中点,知AE=EF=FB,AO=DO.则又D为BC中点,则同理则故

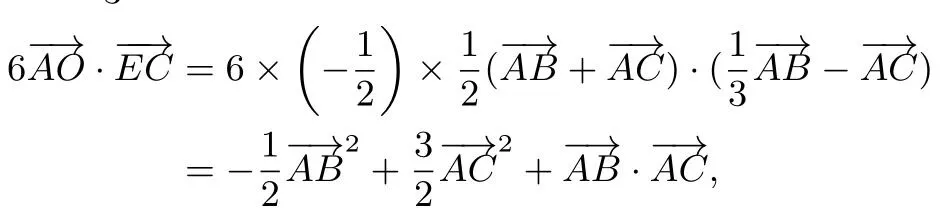
评注利用三点共线模型为平面内一组基底,为平面内任意向量,当且仅当λ+µ=1时,P、A、B三点共线),简化了运算过程,考查了模型素养、逻辑推理、数学运算等核心素养.

三 正难则反

正难则反策略是逆向思维的体现.逆向思维是指从问题的反面进行思考,从而寻求解决问题的方法.正难则反策略消除了习惯于一个方面思考问题的思维局限,构建了事物之间的可逆性和对立性.

例4(2019年高考江苏卷第6题)从3 名男同学和2 名女同学中任选2 名同学参加志愿者服务,则选出的2 名同学中至少有1 名女同学的概率是____.

解选出的两名同学没有女生的概率为故选出两名同学至少有1 名女生的概率为

评注此题从正面思考时需要就选出的两名同学中有1名女同学和2 名女同学进行分类讨论,略显繁琐.从事件反面入手,只需考虑事件选出的两名同学没有女生发生的概率,简洁有效,可快速获解.

四 数形结合

华罗庚指出:“数缺形时少直观,形少数时难入微;数形结合千般好,隔离分家万事休.”运用数形结合思想解题,实现数与形的相互关联,形象直观,有利于提高解题效率.

例5(2019年高考全国Ⅱ卷文科第12题)设F为双曲线C:的右焦点,O为坐标原点,以OF为直径的圆与圆x2+y2=a2交于P、Q两点.若则C的离心率为().

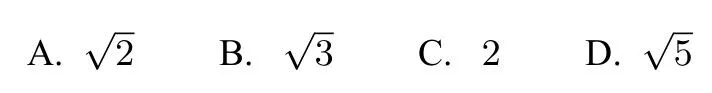
解设F(c,0),因为以OF为直径的圆与圆x2+y2=a2交于P、Q两点,且则故即2a2=c2,所以

图4

评注通过数形结合,将零散、抽象的代数信息用图形语言集中、直观呈现出来,借助“形”的直观性弥补“数”的抽象性,降低求解难度,减少运算过程,体现了多想少算的理念.

五 特殊化

特殊化策略指解决问题时从特殊的情况加以考虑,进而探求问题一般属性的数学方法.运用特殊化策略解题,可简化问题解决的思考方式,优化解答过程,提升解题效率.

例6(2019年高考上海卷第16题)已知tanα·tanβ=tan(α+β),有下列两个结论:存在α在第一象限,β在第三象限;存在α在第二象限,β在第四象限,则().

A.均正确B.均错误

C.对错D.错对

解令由得则β在第二、四象限,故错; 令同理得则存在β在第四象限,故对.

例7(2019年高考全国Ⅲ卷文科第12题)设f(x)是定义域为R的偶函数,且在(0,+∞)单调递减,则().

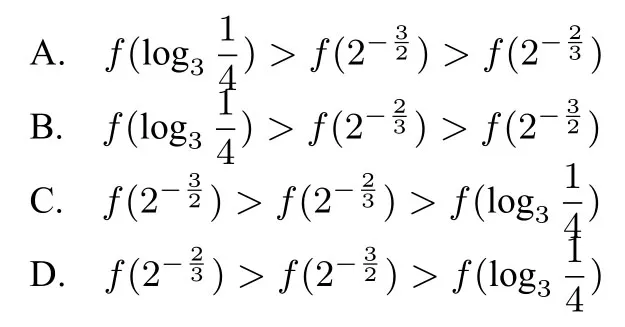
解设f(x)=-|x|,则

评注华罗庚指出:“善于退,足够地退,退到最原始而不失重要性的地方,是学好数学的一个诀窍.”特殊化求解是解答以上两例的最佳方式,充分体现了退的思想.

六 极限策略

极限策略是利用极限思想去分析问题并解决问题的方法.利用极限思想,把问题逼近到某一极端状态,往往能够起到化繁为简的作用.

例8(2019年高考全国Ⅱ卷文科第21题(节选))已知函数f(x)=(x-1)lnx-x-1.证明:

(Ⅰ)f(x)存在唯一的极值点.

解因为且y=lnx单调递增,单调递减,故f′(x)单调递增.当x→0时,f′(x)→-∞;当x→+∞时,f′(x)→+∞,则必存在唯一的x0∈(0,+∞),使得f′(x0)= 0,即f(x)存在唯一的极值点.

例9(2019年高考全国Ⅱ卷理科第20题(节选))已知函数

(Ⅰ)讨论f(x)的单调性,并证明f(x)有且仅有两个零点.

解因为(1,+∞),故f(x)在(0,1)和(1,+∞)单调递增.由f(x)=则x→0时,f(x)→-∞,x→1-时,f(x)→+∞;x→1+时,f(x)→-∞,x→+∞时,f(x)→+∞.则在(0,1)和(1,+∞)上分别存在唯一的x1,x2,使得f(x1)= 0,f(x2)= 0,即f(x)有且仅有两个零点.

评注以上两例用极限对函数图像趋势进行了分析,避免了对零点两侧单调性的讨论,简化了解题过程.

七 猜想策略

猜想策略是解题者根据自身知识储备、解题经验、思维方式,结合问题条件或实验现象、数据等,对研究对象的性质或可能存在的结果进行大胆、合理的猜想.[4]牛顿指出:“没有大胆的猜想,就做不出伟大的发现.”因此,在解题过程中,可以根据实际情况做出合理猜想.

例10(2019年高考北京卷文科第8题)如图5,A,B是半径为2的圆周上的定点,P为圆周上的动点,∠APB是锐角,大小为β.图中阴影区域的面积的最大值为().

A.4β+4 cosβB.4β+4 sinβ

C.2β+2 cosβD.2β+2 sinβ

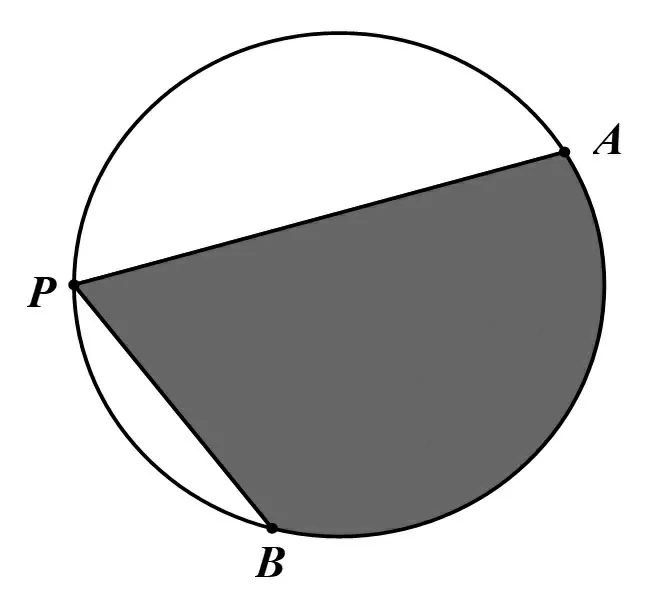
图5

解由圆的对称性,猜想PA=PB时,阴影面积最大.因为阴影部分面积等于弓形面积与ΔAPB面积之和,当点P运动时,弓形面积不变,ΔAPB面积变化,所以当ΔAPB边AB上的高最大时,阴影部分面积最大,如图6.故

S阴影=S扇+2S△P OB,又∠POB=π-β,由解得PB=则2S△P OB=r2sinβ,故S阴影=βr2+r2sinβ=4β+4 sinβ.

评注本例抓住问题的变量与不变量,根据圆的对称性做出初步猜想,进而得出面积最大值.特别指出,猜想不同于空想,而是根据已知条件进行合理的猜想.

八 换元策略

换元策略是指在解决问题的过程中用一个新变量替换原问题中的变量,以减少变量个数、降低变量次数,从而将原问题中复杂结构简单化、明朗化的方法.常见的换元方法有三角换元、整体换元、对称换元、均值换元等.[4]

例11(2019年高考全国Ⅰ卷文科第15题)函数最小值为____.

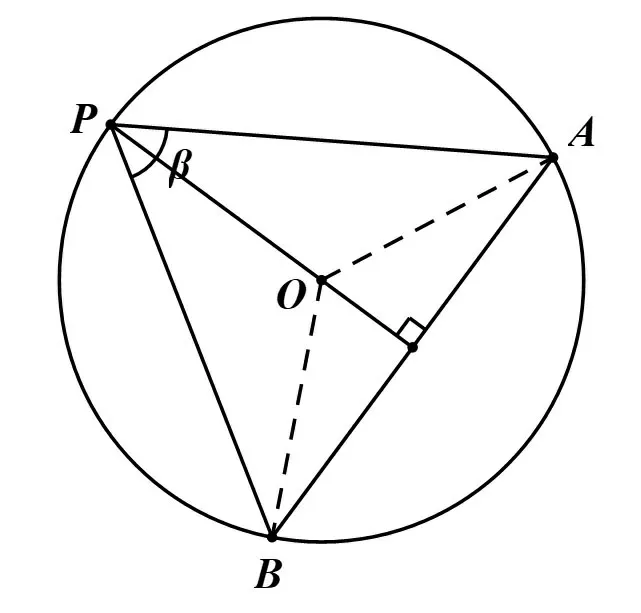
图6

解由

令t=cos x,则t ∈[-1,1],故f(t)=-2t2-3t+1.易得,当t=1,即cos x=1时,f(x)的最小值为-4.评注利用换元法将问题转化为二次函数在闭区间上的最值问题是解答本例的关键.

九 设而不求

设而不求指增设辅助元,但解题过程中不求出辅助元,最终实现问题解决的方法.设而不求往往能避免盲目推演而造成无益的运算,从而达到准确、快速、简捷的解题效果.[5]

例12(2019年高考全国Ⅲ卷文科21题)已知曲线D 为直线上的动点,过D 作C的两条切线,切点分别为A,B.

(Ⅰ)证明:直线AB 过定点.

解设则由则y′=x,故 切 线kDA=x1,则即2x0x1-2y1+1=0.同理,2x0x2-2y2+1=0,故直线AB的方程为2x0x-2y+1=0,故直线AB 过定点

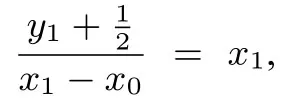
评注证明直线AB 过定点,前提是求出AB的方程,要求AB的方程,常规方法要先求出A,B 坐标,再利用点斜式法求方程,但过程较为繁琐.通过导数的几何意义分别建立过A,B的直线方程,再得出A,B 同时满足的方程2x0x-2y+1=0,进而求出定点坐标,充分体现了设而不求的策略.

十 分离变量

分离变量是解答含参函数不等式恒成立问题的常用方法:分离参数,将问题转化为求函数值域(最值)问题.分离变量可以规避分类讨论带来的繁琐计算.

例13(2019年高考天津卷理科第8题)已知a ∈R,设函数

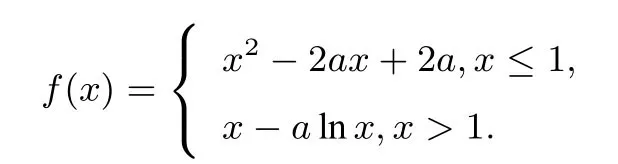
若关于x的不等式f(x)≥0 在R 上恒成立,则a的取值范围为().

A.[0,1] B.[0,2] C.[0,e] D.[1,e]

解(1)当x ≤1时,x2-2ax+2a ≥0 恒成立,若x=1,则1 ≥0,不等式恒成立;要使x<1时,x2-2ax+2a ≥0 恒成立,则设得则g(x)在(-∞,0)单调递增,在(0,1)单调递减,故当x=0时,g(x)max=g(0)=0,得a ≥0.

(2)当x > 1时,x-alnx ≥0 恒成立,即恒成立.设得则h(x)在(1,e)单调递减,在(e,+∞)单调递增,则当x=e时,h(x)min=h(e)=e,得a ≤e.

综上,a的取值范围为[0,e].

评注通过分离变量,将问题转化为函数最值问题.分离变量避免了因二级分类带来的繁琐计算,简化了运算过程.

文中介绍了十种多想少算的解题策略,充分展示了多想少算的魅力.当然,多想少算的解题策略远不止文中的十种类型,可结合具体的高考试题来提炼和开发.