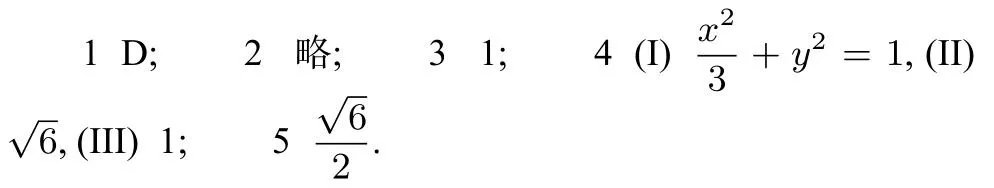小议整体代换法

北京师范大学出版集团

整体代换法在高考、中考中频频有所考查.一些简单层面的应用,本文不再涉及,例如

例1(2014年中考山东省淄博市卷第6题)当x=1时,代数式ax3-3bx+4的值是7,则当x=-1时,这个代数式的值是().

A.7 B.3 C.1 D.-7

例2(2011年高考广东卷文科第12题)设函数f(x)=x3cosx+1,若f(a)=11,则f(-a)=____.

本文仅就一些有趣的整体代换,略作说明,抛砖引玉,供同仁、学子们欣赏.

例3(1979年高考全国卷理科第1题)若(z-x)2-4(x-y)(y-z)=0,求证:x,y,z成等差数列.

简证由已知[(x-y)+(y-z)]2-4(x-y)(y-z)=0,所以(x-y)2-2(x-y)(y-z)+(y-z)2=0.即[(x-y)-(y-z)]2=0.故x+z=2y,所以x,y,z成等差数列.

评注 (1)本题用到代换x-z=(x-y)+(y-z).

(2)也可用乘法公式打开得证,涉及(a+b+c)2公式或分组分解法.

例4(人民教育出版社人教B版第104页第4题)已知:圆的直径端点是A(x1,y1),B(x2,y2),求证:圆的方程是(x-x1)(x-x2)+(y-y1)(y-y2)=0

简证由已知可得圆心直 径方 程 是即

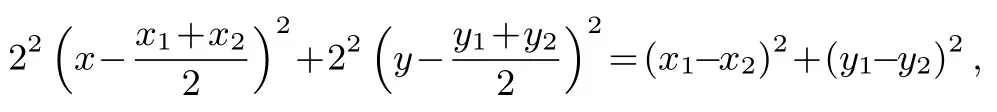
即

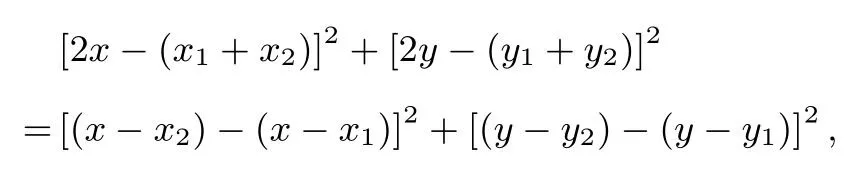
即 [(x-x1)+(x-x2)]2+[(y-y1)+(y-y2)]2

=[(x-x2)-(x-x1)]2+[(y-y2)-(y-y1)]2,

即 [(x-x1)+(x-x2)]2-[(x-x2)-(x-x1)]2

=[(y-y2)-(y-y1)]2-[(y-y1)+(y-y2)]2,

所以(x-x1)(x-x2)+(y-y1)(y-y2)=0.

评注 (1)本题用到2x-(x1+x2)= (x-x1)+(x-x2),x1-x2=(x-x2)-(x-x1),类似处理2y-(y1+y2),y1-y2.

(2)公式背景(a+b)2-(a-b)2=4ab.

(3)向量法等方法证略.

例5(1999年高考全国卷理科第8题4分)若(2x+则(a0+a2+a4)2-(a1+a3)2的值为().

A.1 B.-1 C.0 D.2

简解令x=1 得

令x=-1 得

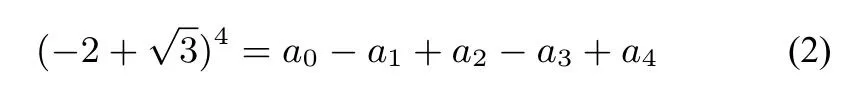
由(1)(2)得

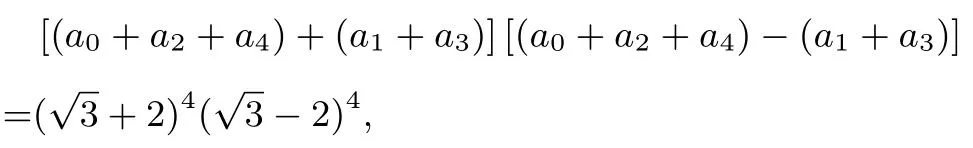
即

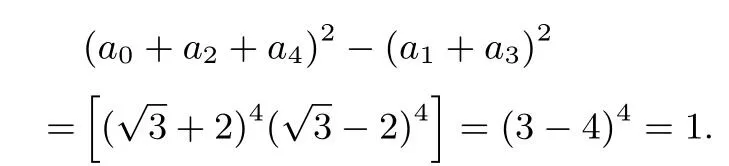
故选A.

评注(1)本题将a0+a2+a4及a1+a3分别看成是一个整体,用平方差公式即得.

(2)(a0+a2+a4)2-(a1+a3)2= (a0+a1+a2+a3+a4)(a0-a1+a2-a3+a4)与已知的二项式展开式类比,需分别令x=1,-1.

例6(2016年高考北京卷理第19题)已知椭圆的离心率为A(a,0),B(0,b),O(0,0),ΔOAB的面积为1.

(Ⅰ)求椭圆C的方程;

(ⅠⅠ)设P是椭圆C上一点,直线PA与y轴交于点M,直线PB与x轴交于点N.求证:为定值.

简解(Ⅰ)

(ⅠⅠ)设P(x0,y0),则x20+4y20=4.由已知设M(0,m),N(n,0).由已知可得A(2,0),B(0,1).由kP A=kAM得即所以BM=

由kP B=kBN得即所以所以又x20+4y20=4,所以

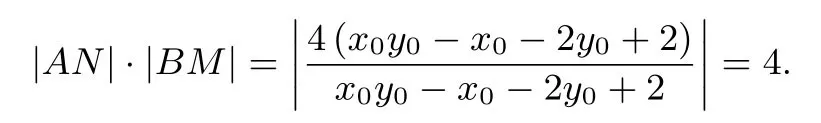
评注(1)本题也是两次用到了整体代换:x20+4y20=4,及x0y0-x0-2y0+2 作为一个因子整体约分了.

(2)平面解析几何的原则之一:尽可能地少设字母.本题不得已先设了x0,y0,m及n,挖掘隐含条件(两组三点共线)后,分别用x0,y0表示了m,n,减少了字母的个数.但具体的x0,y0的值还是求不出来的,只能寄希望于整体代换了.

练习1(2011年天津中考)若实数x,y,z满足(x-z)2-4(x-y)(y-z)=0,则下列式子一定成立的是().

A.x+y+z=0B.x+y-2z=0

C.y+z-2x=0D.z+x-2y=0

练习2求证:过圆(x-a)2+(y-b)2=r2上一点(x0,y0)的该圆的切线方程为(x0-a)(x-a)+(y0-b)(y

b)=r2.

练习3(2006年湖北省荆门市中考)若a0+a1x+a2x2+a3x3,则(a0+a2)2-(a1+a3)2的值为____.

练习4(2018年高考北京卷文第20题)已知椭圆的离心率为焦距为斜率为k的直线l与椭圆M有两个不同的交点A,B.

(Ⅰ)求椭圆M的方程;

(ⅠⅠ)若k=1,求|AB|的最大值;

(ⅠⅠⅠ)设P(-2,0),直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点共线,求k.

练习5已知A,B,P是双曲线上不同的三点,且A,B两点关于原点O对称.若直线PA,PB的斜率则该双曲线的离心率为____.

答案