触类旁通 融会贯通——以《省刻度尺》教学为例

○蒋守成

数学主题拓展教学有三个基本要素：主题、拓展、思维。主题是思维的起跑线，拓展是思维的发动机，目标是促进学生形成结构化的思维方式。在这样的教学范式下，学生的思维方式有了很大的变化，特别是在结构化的思维方式上有了很大的提升，能够将从一课习得的思想方法运用到相类似或者紧密联系的某一类数学问题中，学会举一反三、触类旁通，从而达到融会贯通。

课前思考

选择以《省刻度尺》为主题进行拓展教学，主要是基于以下四个方面的思考：一是省刻度尺问题既是“以少表示多”的典型问题，也是华罗庚统筹优化思想的具体表现；二是省刻度尺的研究适合学生去自我探究和发现，可以为学生的后续学习服务，为解读生活中的优化现象提供经验；三是省刻度尺的教学是对人教版教材四年级上册数学广角“统筹、优化”学习内容的拓展；四是通过省刻度尺的学习，学生对生活中相关联的一类问题形成结构化的思考。

教学过程

一、聚焦主题，经历过程，发展思维

（一）经历数学家一样的探究过程，明晰什么是省刻度尺。

1.共同探究省一个刻度的情况。

师：今天的数学研究从一把5厘米长的直尺开始。

0 1 cm 2 3 4 5提问：用这把直尺量出3厘米，可以怎么量？生：从0量到3就可以量出3厘米。提问：刻度3被老师省掉了（如下图），你还能用这把直尺一下子量出3厘米吗？说说你是怎么想的。0 1 cm 2 4 5

生1：先从刻度0量到刻度2，量出2厘米，然后再量出1厘米。

生（评价）：这样量不符合用这把直尺一下子量出3厘米的要求。

生2：我们可以从刻度1量到刻度4，因为1到4之间是3厘米。

生3：我们也可以从刻度2量到刻度5，因为2到5之间也是3厘米。

师：虽然没有刻度3，但我们改变了测量方法，由一直从刻度0开始量改成从刻度1或2开始量，打破了固有的习惯。同学们，我们有的时候解决问题也要打破常规，换一个角度思考就会找到解决问题的新路径。现在我们将测量3厘米的方法记录下来：3（1～4）（2～5）。请同学们将其他刻度也用这种方式表示出来。

2．自主探究省两个刻度和省三个刻度的情况。

师：省掉一个刻度，我们照样能一次量出所有刻度对应的长度。如果这把5厘米的尺子省掉两个刻度或三个刻度，你觉得还能不能一次量出所有刻度对应的长度呢？我们一起来研究：

（1）问题：下面这两把直尺一次能量出哪些长度？先想一想，然后把你能量出的所有长度清楚地记录在作业纸上。

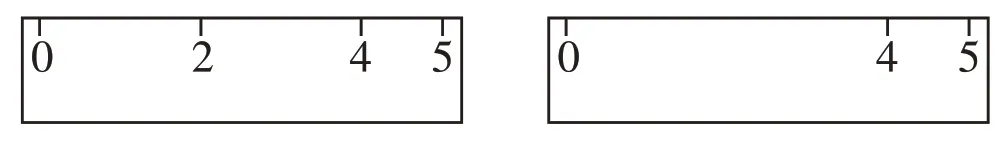
（2）比较：我们分别研究了5厘米的刻度尺省掉一个刻度、省掉两个刻度都能够一次量出所有刻度对应的长度，而省掉三个刻度就不能全部量出来。你觉得哪把直尺上的刻度省得恰到好处？说说你的想法。

（3）分享：省一个刻度虽然可以一次量出1到5厘米之间任意一个整厘米的长度，但是用到的刻度还是多了一个，不是最省刻度的；省三个刻度，1到5厘米之间有些整厘米的长度无法一次量出来，显然是刻度省得太多了；省两个刻度不仅能够一次度量出1到5厘米之间任意一个整厘米的长度，而且用到的刻度也是最省的，所以这把直尺上的刻度省得恰到好处，是最神奇的。

3.明晰什么是省刻度尺。

（1）命名：如果给这把最省刻度的直尺起个名字，你会把它叫什么呢？

生1：神奇的尺子。

生2：奇妙尺。

生3：少刻度的尺。

（2）由来：其实早在100多年前英国数学游戏大师杜登尼就发现了这种特殊的刻度尺，并命名为“省刻度尺”，我们一起来看一段微视频。

一根23厘米长的尺子，通过最省、最优的办法只需六个刻度（头尾不用刻），就能够度量出1到23之间任何整厘米长的物品。如果减少一个刻度就不能量出所有整厘米的长度，如果增加一个刻度就不是最省，我们把这种尺称为“省刻度尺”。

（3）标准：什么样的刻度尺才是省刻度尺？标准是什么？

学生通过讨论得到：不仅能一次量出所有长度中的任意一个，而且刻度最省。

（4）判断：下面的刻度尺是不是省刻度尺？

下面是一把7厘米长的直尺，0和7之间只有两个刻度，它是不是一把省刻度尺呢？先把能量出的长度有序地记录在作业纸上，然后再想一想它是不是省刻度尺。

生：不能量出3厘米，所以不是省刻度尺。

师：根据老师的研究，0和7之间至少要有三个刻度才能成为省刻度尺，那么再添一个刻度使它成为一把省刻度尺，请你添一个并把记录补充完整。

生：添3，就可量出3厘米，（0，2，3，6，7）。

生：添4，4到7是3，（0，2，4，6，7）。

生：添5，2到5是3，（0，2，5，6，7）。

师：同样是缺3厘米，添的数不同，得到的省刻度尺也不同。看来解决这个问题的答案不止一种，我们不能把“之一”当“唯一”。其实，这把直尺添上三个刻度成为一把省刻度尺还有更多的方法：除了从1开始想，（0，1，2，5，7）、（0，1，3，5，7）、（0，1，4，5，7）；还可以从2开始想，（0，2，3，6，7）、（0，2，4，6，7）、（0，2，5，6，7）；也可以从3、4开始想，（0，3，5，6，7）、（0，4，5，6，7）……这样有序的思考可以帮助我们找到更多解决问题的办法。带着这样的思考我们一起来创造一把省刻度尺。

（二）引导学生尝试创造一把省刻度尺。

问题：这是一把6厘米长的刻度尺，请你添上最少的刻度，设计成一把省刻度尺。

学生尝试添一添，教师巡视，展示、评价学生的作业，最后同时呈现多种不同的添加刻度的方法。

展示：学生展示自己创造的省刻度尺——（0，1，4，6），（0，2，5，6）。

提问：仔细观察同学添加的这些刻度，你觉得我们在添加这些刻度时有什么方法可循吗？

分享总结：不管添加哪两个数，四个数中至少要有两个数是相邻的，然后我们可以再进行比较和调整，达到最省的标准。

让学生自己设计一把省刻度尺，在设计的过程中体验省的方法和策略，为进一步研究省刻度尺是否存在一般规律的问题提供经验。

二、触类旁通，全面体悟省的学问和省的智慧

问题一：量角器上的省刻度。

师：直尺上的刻度省了照样可以量出所有的刻度，那量角器上的刻度可不可以省呢？（出示：一个不完整的量角器）利用这个量角器可以一次量出哪些度数的角？同学们先独立思考，然后同桌交流，形成共识后向全班展示。

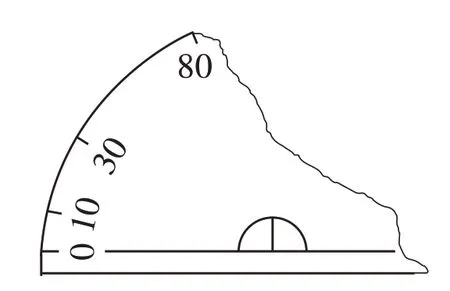
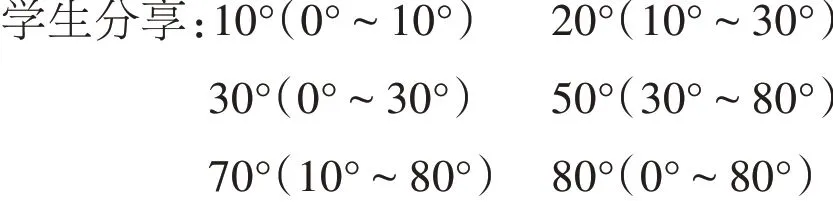
追问：除了可以量出以上这些度数外，还可以量出哪些度数？

学生讨论得出:还可以从右边180度考虑，例如量出170°（10°～180°），150°（30°～180°）……

问题二：人民币中的省面额。

师：我们在研究直尺、量角器的过程中发现，虽然刻度省了，但照样能量出更多的长度或角度。省不仅是一种学问，省也是一种智慧。除了省刻度，我们经常用的人民币中也用到了省的智慧。

同学们，你知道吗？为什么常见的小额面值的人民币只有1元、2元、5元和10元，而没有3元、6元等其他面值呢？

生1：用1元、2元、5元进行加减运算就可以得到另外一些数，如1+2=3，2+2=4，1+5=6，2+5=7，10-2=8，10-1=9等。

生2：现在2元的人民币都省掉了，只是运算次数多了而已。

微视频介绍：为什么常见的小额面值的人民币只有1元、2元、5元和10元这四种？

抓住“省刻度尺”的本质，同时结合生活实际进行拓展，延伸到同类问题，进行触类旁通的学习，让学生进一步体会到省的智慧、省的学问。

课后思考

这节课是以省刻度为主题，培养了学生独立思考和自由探索的数学品质。学生感受到了以少表示多的神奇之处，习得了省的学问，同时拓展了对统筹和优化思想的认识，为后续学习优选法和统筹法中最优化等问题打下基础。例如，学生学完省刻度就能理解和解释其他相邻的两个面积单位的进率都是100、而公顷和平方米的进率却是10000的道理，原来中间省了一个面积单位公亩。关于人民币的面值，学生还会思考：中国古代货币的面值是怎样设计的？外国货币的面值是怎样设计的？未来的货币又会是什么样呢？