几何中角度最值问题的另法探析

广东省深圳市华强职业技术学校

广东省惠州市博罗中学(516100)易 敏

1 常见的角度最值问题

例1点A 与点B的坐标分别是(1,0),(5,0),点P是在该直角坐标系内的一个动点.当点P 在y轴上移动时,∠APB是否有最大值？若有,求点P的坐标,并说明此时∠APB最大的理由;若没有,也请说明理由.

图1

如图1,过点A作AC⊥ PB,垂足为C,设P(0,y),则OP = y,因为∠CBA = ∠OBP,∠BCA = ∠BOP,所以ΔBCA ∽ΔBOP,所以在RtΔACP中,

该题是中学常见的角度最值问题,我们可以发现几何中角度的最值问题往往不是直接用角度进行描述的,通常要利用三角函数进行转化.通过三角函数的解析式分析,求出三角函数的最值,再利用角度与三角函数的关系,从而达到求解角度最值的目的,这种方法我们称为三角函数解析法.三角函数解析法的优点是方向很明确,分析所求角的三角函数解析式的最值,利用三角函数的单调性,从而分析出角的最值.但其难点和关键就在于三角函数解析式的求解和分析,当三角函数解析式较为复杂时,就难以判断三角函数的最值了.

另法探析既然三角函数解析式的求解和分析是一个难点,那么我们是否可以绕开求解三角函数解析式？那角度的描述还有什么途径呢？在平面几何中,我们还学习过相关角.只要我们找到相关角以及确定的相关关系,那么求解相关角的最值,进而就能够分析出所求角的最值了.问题的关键就转化为求解相关角了,而不用三角函数解析法又如何描述相关角的最值呢？下面我们先了解两个结论.

结论1等腰三角形底边长不变,底边上的高越长,顶角越小.反之,顶角越大.

图2

结论2不共线的三点确定一个圆.

如图 3,设P(0,y)(y /= 0),过A,B,P三点做一个圆,圆心为O 易知圆心O 在线段AB的中垂线上,可设O(3,n),AP中点由可得点O的坐标为

图3

在圆O中,2∠P = ∠AOB,在等腰三角形OAB中,点O是随点P的变化而变化的,则底边上的高当且仅当即时,h最小,顶角∠AOB最大,∠P也最大.故当P点的坐标为时,∠P最大.

利用不共线的三点确定一个圆的结论,成功将点P的运动转化为圆心O的运动,这一转化的前提是另外两点A,B是定点,而角度的最值问题常常就是符合这样条件的,这是该方法的巧妙之处.在动圆O上,动角∠P正好与动角∠AOB有相关关系2∠P=∠AOB,这是构造三点圆最巧妙的地方.先判断∠AOB的最值,利用2∠P=∠AOB,即可得到∠P的最值.而∠AOB在等腰三角形AOB上,这又是构造三点圆又一巧妙之处.利用结论1,将∠AOB的最值判断转化为等腰三角形底边高h的最值判断,就成功的绕开三角函数解析式的复杂求解和分析了.而高h的求解即是圆心O的纵坐标的绝对值,这是比较容易计算和分析.总的来说,这种方法思维十分巧妙,但思路确是值得探究的,利用构造三点圆,将已知动点转为相关动点,将已知动角转化为相关动角,从而更加简化了三角函数解析法的计算和分析.当然这种方法不仅仅适用于这个题,我们再来看看点P的圆锥曲线上运动的情况.

2 圆锥曲线上的角度最值问题

例2如图4,已知点P是椭圆上一动点,A、B分别为左、右顶点,求证点P在什么位置时,∠APB最大.

图4

设点P(x,y),A(-a,0),B(a,0)则kP A=所以

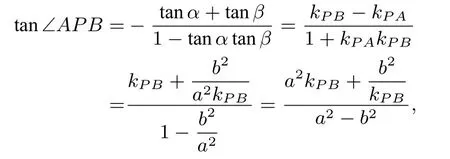
由对称性不妨设点P在第一象限及C点,则有kP B ＜0,故tan ∠APB=当且仅当时,等号成立,即时,tan ∠APB取最大,即∠APB最大,也就是点P在顶点C处,∠APB取得最大值,同样点P在椭圆下顶点处时,∠APB也取得最大值.

该解法就是常用的三角函数解析法,其亮点在于将直线的斜率作为变量描述所求角的三角函数,也是该解法的精辟之处.虽说比直接用点P的坐标作为变量更加简便,但其计算量并不会因此而减少多少,利用此解法还是逃不过三角函数解析式的求解和分析.

经计算得出该教材整套AWL覆盖率为4.63%，介于1.4%和10%之间，即该《新视野》既不属于通用英语也不属于学术英语，更偏向于通用英语。由图5知，《新视野》四册书的AWL覆盖率变化范围由3.67%到5.41%，介于通用英语和学术英语文本之间。但整体在平均AWL覆盖率4.63%上下波动。同时，图5表明，四册书的AWL覆盖率变化值波动幅度显著，《新视野》教材的AWL覆盖率并未呈现出由低到高、循序渐进的理想状态。因此，可做出相对调整，如第一册与第三册可调换位置，第二册与第四册调换位置。

不妨设点P在第一象限及C点,由A,B,P不共线可知,存在圆O′过A,B,P三点,且圆心O′在y轴负半轴上,在圆O′中,有∠APB=先求圆心O′的坐标,设P(x,y),B(a,0),中点由可得,由则y越大,越小,等腰三角形O′AB的高O′O越长,∠AO′B越小,∠APB越大,则当y=b,即点P在C点处,∠APB取最大,同样点P在椭圆下顶点处时,∠APB也取得最大值.

图5

该种解法同样是构造三点圆,分析相关点、角的最值进而得出所求角的最值,该种方法比起三角函数解析法在计算方面要简便很多,而且这道题利用这个思路可以分析,动点P从B移动到C的过程中,圆心O′在y轴负半轴越来越远离原点O,∠AO′B越小,则∠APB越大.所以单从思路分析来看,这种方法更容易得出结论,可以直接判断出∠APB取最大值时,点P的位置.

3 研究结果

从例1和例2的分析求解过程,可以发现它们都是定线段所对动角的最值问题,这一类问题可以利用构造圆去解决,而这种独特方法的精髓之处是:

(1)思路:动点影响变量(长度、角度、面积等)的最值问题,抓住动点的特点,找出其相关点,分析相关点的动态对所求变量的影响;

(2)技巧:构造不共线三点圆,从而将原动点转化为圆心的分析.

利用这种思路和技巧,可以解决定线段所对动角的最值问题.反之,通过研究可以发掘出类似的定线段所对动角的最值问题,丰富几何中角度最值问题.比如下面两个变式,以圆锥曲线为载体的角度最值问题,可以通过三角函数解析法去求解,也可利用构造圆去求解,而且还涉及到不等式,正是能够综合考查高中学生的数学思维能力和分析解题能力.

变式1在O为原点的平面直角坐标系中,抛物线C:y2=8x的焦点为F,点P是该抛物线上的一个动点,问:∠OPF是否有最大值？若有,求点P的坐标;若没有,请说明理由.

变式2在O为原点的平面直角坐标系中,点到直线l:x=4的距离和它到定点F(1,0)的距离的比是常数4,点P是直线l上的动点.

(1)求M的轨迹方程;

(2)∠OPF是否有最大值？若有,求点P的坐标; 若没有,请说明理由.

4 研究发展与改进方向

本次研究仅是对平面几何的角度最值问题简单分析,并从中得到一种新的方法去解决角度最值问题,当然这种方法适用性确实有所局限,但是方法中的思想和思维方式,是解决其他动点问题应当借鉴的.动点问题涉及不止角度最值问题,还有长度,面积等相关问题,在今后的的研究中,希望有机会能利用文中的想法和思维去解决解析几何特别是圆锥曲线的动点问题.除了平面几何,在立体几何方面,同样也有相关的动点问题,希望热爱数学的研究者能够利用这个思维方式去解决更多问题.同样,除了构造三点圆,线段中点等将原动点转化为相关点分析的方法之外,希望能够找到更多更有实用价值的方法,以丰富几何动点问题的解法.