二次函数与必修一教学的五次“邂逅”

广东省广州大学附属中学

二次函数是贯穿高中数学的一种非常重要的函数,也是连接初中和高中数学的重要纽带,尽管初中有学习过二次函数,但多是浅显和机械式的学习,不能从本质上加以理解.进入高中后,还需进行深入再学习,而人教版必修一教材并没有专门去讲二次函数,这就需要我们在必修一的教学过程中,有目的去渗透二次函数的知识.那么该如何渗透,笔者谈谈自己的一些做法.

渗透一一元二次不等式的解法.在必修一集合,函数定义域、值域等相关问题不可避免的需要解一元二次不等式.在高一开学初渗透相关知识,有助于做好初高中知识衔接,帮助学生掌握解一元二次不等式的基本技能,有助于必修一的函数学习.

回顾初中二次函数知识,引导学生总结出解二次不等式一般ax2+bx+c (a ＞0)＞0 或ax2+bx+c (a ＞0)＜0的步骤:

1.求出方程的根的判别式,判断方程的根的情况(若有根的求出实数根);

2.画出二次函数的草图(尤其是图象与x轴的交点情况);

3.由图得不等式的解集.(看图说话)

帮助学生总结:以a ＞0为例,填写如下的表1,其中二次项系数不为1的因式分解,二次项系数为负的解不等式,作为难点和易错点需重点突破,此过程中渗透的思想方法:函数思想、数形结合、化归转化.

表1 不等式的解集

渗透二二次函数在区间上的最值.在学习完函数基本性质后,学生对最值、值域、单调性等知识有所理解,此时渗透二次函数最值相关知识,可以让学生体会数形结合思想,加深理解由单调性求最值的基本方法,建立简单的分类讨论意识.

典型例题(1)画出函数f(x)=3+2x-x2的图象;

(2)结合图象分别求出函数在下列区间上的最大、最小值.

1)x ∈[-1,0]2)x ∈[-1,3]3)x ∈[t,t+1]

方法感悟

1)f(x)在[-1,0]单调性____,f(x)最大值____,最小值____;

2)f(x)在[-1,3]单调性____,f(x)最大值____,最小值____;

3)题由于不明确对称轴x = 1是否在区间[t,t+1]内,因此要分三类:

第一类:x = 1 在[t,t+1]的左边:即t ≥1,画出草图,f(x)单调性____,f(x)最大值____,最小值____;

第二类:x = 1 在[t,t+1]内:即t ＜1 ＜t+1,即____;(注意:本题求最小值要继续分类)

第三类:x=1 在[t,t+1]右边:即t+1 ≤1,即____;

通过典型例题引导学生总结二次函数在区间上最值的算法步骤:

第一步:利用“配方法”结合图象得函数的对称轴(或顶点)及函数的单调性;

第二步:判断对称轴(或顶点)是否在所要求的区间内,明确是否需要“分类讨论”;

第三步:利用单调性(图象的直观体现)得最值.

变式1已知函数f(x)=x2-2ax+2,其中x ∈[-1,2].

(1)若函数f(x)在[-1,2]上单调递增,则实数a的取值范围为____;

(2)若函数f(x)在[-1,2]上单调,则实数a的取值范围为____;

(3)若f(x)≥a 恒成立,求实数a的取值范围;

(4)若存在x 使f(x)≥a 成立,求实数a的取值范围.

变式2已知a/=0,函数f(x)=ax2-2ax+1 在[-1,2]上的最大值为M(a),求M(a)的表达式.

例题设置可层层递进,其中含字母的配方,二次项系数含有参数,准确寻找讨论依据,是本部分的重难点,需根据班级实际情况,设置不同层次的难度,通过典型例题,逐步突破.

渗透三二次函数的图像变换.在学习完指对数函数后,需要补充函数图像变换的相关知识,二次函数图像的相应变换可渗透其中,这时以二次函数为背景,讲解对称、翻折、平移等变换,有助于学生对图形变换的理解.

典型例题(1)画出曲线y = x2-x 及y = x2-|x|的图像.

(2)若直线y = 1 与曲线y = x2-|x|+a 有四个交点,求实数a的取值范围.

分析直线y =1 与曲线y =x2-|x|+a 有四个交点⇔方程1 = x2-|x|+a 有四个实数根(先不要着急画草图,再移项变形试试)

⇔方程____有四个实数根

⇔直线y =1-a 与曲线y =____有四个交点.

变式1若直线y =1 与曲线y =|x2-x|+a 有四个交点,实数a的取值范围为____.

变式2若直线y =1 与曲线y =(x-1)2-|x-1|+a有四个交点,实数a的取值范围为____.

变式3设定义在R 上的函数f(x)= -x2+3x-2,若方程|f(x)|-kx-k =0 有四个不同的实根,则实数k的取值集合为____.

在此过程中,学生不仅可以通过二次函数加深对基本图像变换的理解,还可以体会方程的根与函数图像交点个数的互相转化.

渗透四二次函数的零点分布.在学习完函数零点相关知识后,渗透二次函数的零点分布,有助于加强对零点概念的理解,帮助学生掌握二次函数零点分布的代数转化.

二次方程根的分布可以转化为二次函数的零点分布问题,利用二次函数的图象解决,需用到转化思想、数形结合、零点存在定理.

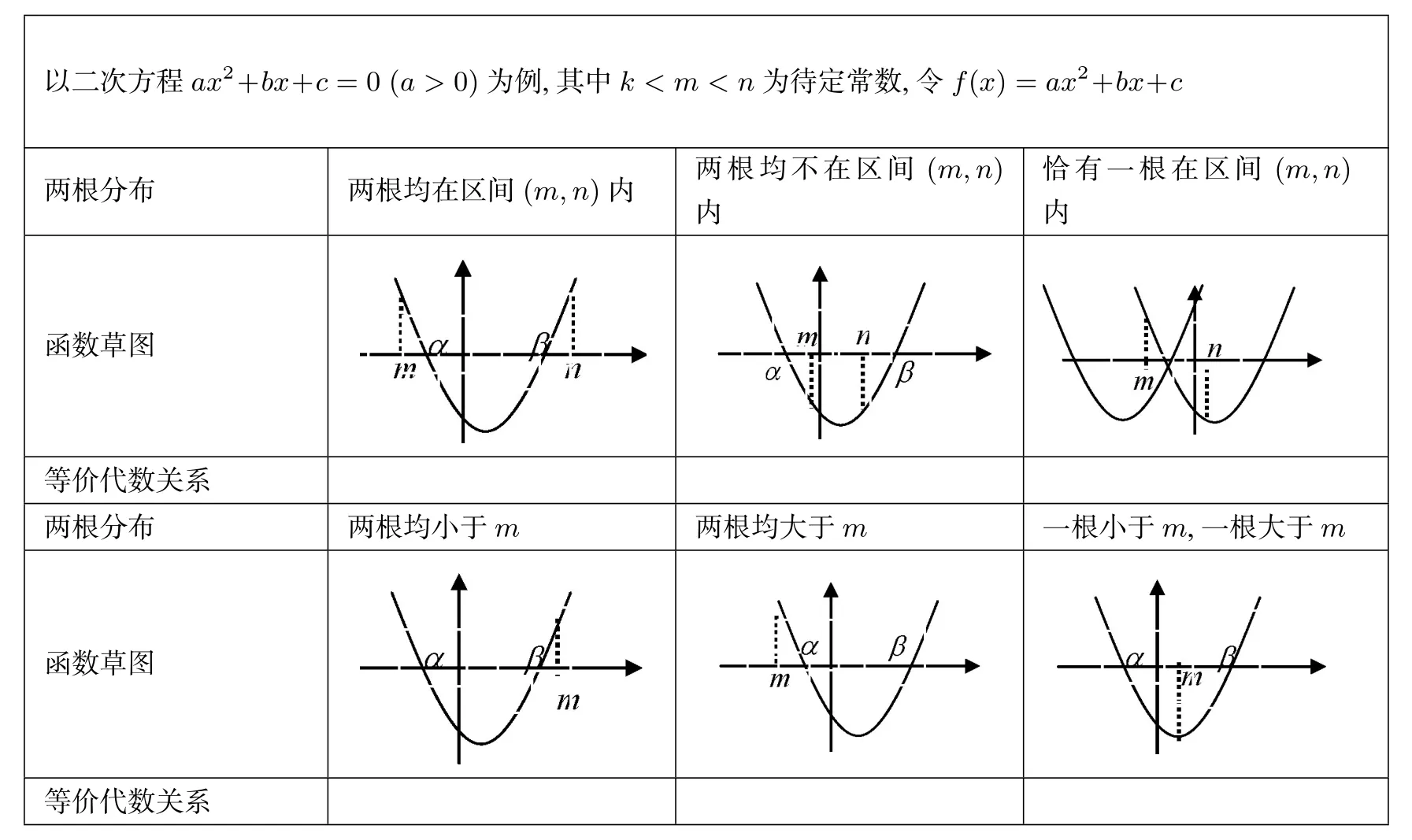
表2 方程的根

典型例题实数m取何值时,关于x的二次方程x2-2(m+2)x+m2-1 = 0 有一根位于区间(0,1),另一根位于区间(1,2)?

变式(1)有一个正根,有一个负根;(2)有两个都大于2的根;(3)有两个都小于2的根;(4)在(0,2)内有一个根;(5)两根都在(0,2)内;(6)两根都不在(0,2)内.

一元二次方程根的分布(二次函数零点分布)总结归纳:

渗透五含参数一元二次不等式及二次函数的综合问题.在必修一结束后,可将前四次渗透的二次函数知识进行拓展和加深,以典型例题增强学生分类讨论意识及能力,重点关注含参不等式的解法与含参分段函数最值的分类讨论.

(1)含参数一元二次不等式解法

典型例题已知a ＞0,解关于x的不等式(3x+2a)(xa)＞0.

变式1已知a ∈R,解关于x的不等式(3x+2a)(x-a)＞0.

变式2已知a ∈R,解关于x的不等式3x2-ax-2a2＞0.

变式3已知a ∈R,解关于x的不等式a(3x+2a)(xa)＞0.

感悟方法严格按照算法步骤,抓住主要矛盾,捕捉分类契机,层层递进,不重不漏！

能力提高充分利用变式教学,帮助学生理解分类讨论本质,提高数学能力！

1.讨论关于x的不等式(x-a2)(x-a)＞0的解集(a为实数).

变式1讨论关于x的不等式x2=-(a+a2)x+a3＞0的解集.

变式2讨论关于x的不等式的解集.

2.讨论关于x的不等式(mx-1)(x-1)＞0的解集(m为实数).

变式1讨论关于x的不等式mx2-(m+1)x+1＞0的解集.

变式2讨论关于x的不等式的解集.

(2)含参数一元二次分段函数的最值

典型例题设a为实数,函数f(x)=x2+2a|x-1|,x ∈R.

(1)讨论函数f(x)的奇偶性;

(2)求函数f(x)的最小值.

分析带有字母的问题,往往要“分类讨论”

当____,f(x)是____函数;用特殊值给予确认;

(2)

推荐方法分对称轴的区间讨论法

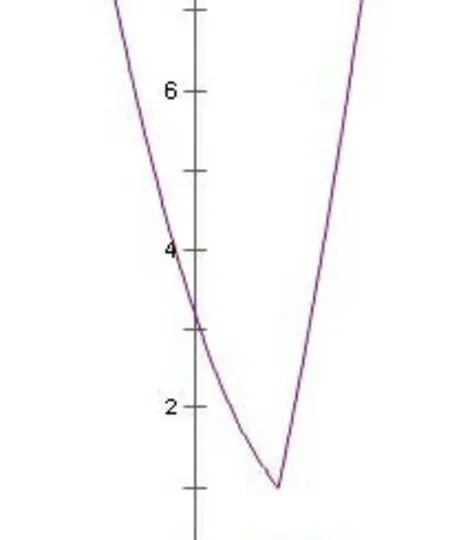
图2: a ≥1

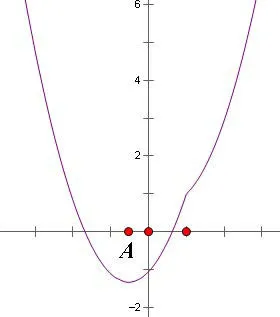
图3: -1 ＜a ＜1

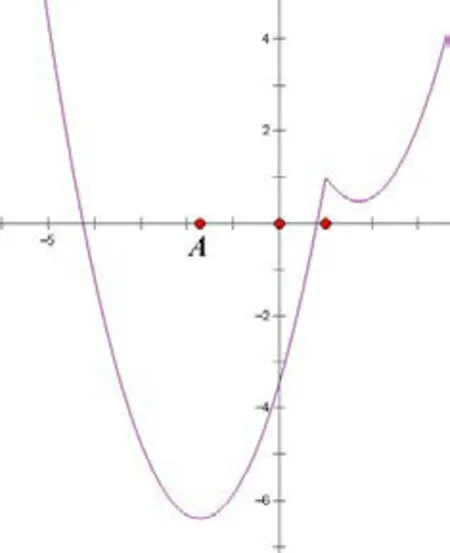
图4: a ≤-1

变式1设a为实数,函数f(x)=x2+|x-a|+1,x ∈R.

(1)讨论函数的奇偶性;

(2)若f(x)的最小值为2,求实数a的值.

变式2函数f(x)=2x2+(x-a)|x-a|.

(1)函数f(x)是否具有奇偶性;

(2)求f(x)的最小值.

其中一元二次不等式的零点分类比较,开口方向,含绝对值的二次函数(分段函数)的最值讨论,都是难点.充分利用变式教学和数学结合的思想,有助于学生突破难点,提升能力.

考虑到必修一教学课时问题,设计这五次渗透时,尽可能以学案的形式呈现,让学生能充分利用课外时间.由于各个学校学生层次不同,在设计每次渗透时,可依据学生水平,设置不同的难度.

二次函数,有丰富的内涵和外延,作为最基本的初等函数,它可以建立起函数、方程、不等式之间的联系.二次函数不仅在必修一中至关重要,在与导数知识结合中,二次不等式,零点与最值更是作为基本的解题工具,需要学生熟练掌握.以上只是笔者自己的一点体会,不足之处请批评指正.