激活思维,方得奥妙—-一堂向量典型问题习题课设计
安徽省安庆市怀宁县新安中学
1 创设情境,引入问题
教师:同学们,之前我们学习了平面向量基本定理,平面向量基本定理告诉我们,平面内任意一个向量都可以用两个不共线的向量量化,这为我们研究问题带来极大的方便.同时,平面向量基本定理也是整个向量理论的基础,所以我们一定要学好这个基础,为后面的学习做好准备,今天我们继续学习有关平面向量基本定理的一些应用.
例1如图1,平面内有三个向量其中与的夹角为120°,的夹角为30°,且若则λ+μ的值为___

图1

图2
教师:大家回顾平面向量基本定理的推导过程,中间作了一条什么样的辅助线? 你能用类似的方法解决这道题吗?
学生1:如图2,过终点C作其中一个基底的平行线交另一个基底OA于点D,则于是λ=4,μ=2,λ+μ=6.
教师:很好,这位同学用了作基底平行线的方法得出了正确答案,而且计算量也不大.请大家积极思考,还有其它的方法吗?
学生3:我用的是建立坐标系的方法,以O为坐标原点,OA为x轴建立平面直角坐标系,写出向量的坐标,代入得到两个关于λ,μ的两个方程,从而解出λ,μ.
教师:非常棒.这道题现在我们有3 种解法,但在实际运用时大家还要注意选择合适的方法.
练习选择合适的方法解答下面这道题:向量a,b,c在正方形网格中的位置如图3所示,若c=λa+μb(λ,μ ∈R),则

图3

图4

图5
教师:让学生思考题中的向量a,b,c是如何给出的? 结合网格的特点,选择适当的方法.
学生4:我用的作基底的平行线法,因为在网格中可以很方便的看出长度的比例关系,如图4,于是
学生5:网格线中的横线和竖线是垂直的,非常适合建系,我用的建系法,如图5.我认为这题建系法比作图法还要简单,因为它只需要写出坐标即可,没有任何技巧,大部分同学在考试中都可以用这种方法解出这道题.
2 师生互动 认识本质
例2:如图6,在梯形ABCD中,AB//CD,AB=2CD,M,N分别为CD,BC的中点,若则λ+μ=___

图6
经过大家的讨论,发现这题的作图法比较麻烦,考试时难以得出正确答案,或者可以特殊化建系法,让AD与AB垂直.
教师:这些方法都是具体求出λ和μ的值,然后再求和.请同学思考一下,数学当中的求和必须要求出每个量的具体值吗? 我们能不能不求出λ和μ的值,而直接整体求出它们的和呢?
大家经过讨论,都认为可以整体求出,因为前面在学习三角函数的时候,在求方程根的和时都是直接运用对称得出和的,而不需要求出每一个根,但这个如何整体求出呢,大家陷入了沉思? 教师适当提示:
教师:前面我们讲到一个关于向量分解系数和的结论,大家还记得吗? 共线定理推论:设O,A,B三点不共线,且若P,A,B三点共线,则λ+μ=1,这道题有推论中这样的模型吗?

图7
如图7,连接MN并延长交AB的延长线与E点,由结论得:(其中x+y= 1),又易得
做完之后,大家惊呼:原来这么方便.
教师:谁能把这个方法的步骤叙述一下?
学生7:第一步:找交点E第二步:把待求向量用表示即可,前面的系数即为所求
教师:大家能把对这道题的做法做一个提炼和推广吗?经过大家的讨论和修改,得出一般性结论:
结论1如图8,O,A,B三点不共线,OP交AB于点C,(x,y,λ为实数),则x+y=λ

图8
证明由结论,(其中m+n= 1)„ 又即得于是x+y=λm+λn=λ.

图9
教师:由此我们可以看出x+y的值完全由中的λ所确定,只要我们找到交点,再把待求向量重新表示.一开始的例1可以用这个方法做吗? 请大家试试看.
教师:这个解法和之前的解法有什么不同?
学生9:之前的解法是单独求出每个系数,再相加,这个解法是直接整体求出和,但不知道具体的每个系数,如果只需要求和还是这个方法方便.
3 小组合作共探新知
教师:现在我们已经知道了如何整体求出向量在基底分解形式下的系数和,现在我让P点动起来(图10),当P点位置变化时,x+y值是怎么变化的呢?
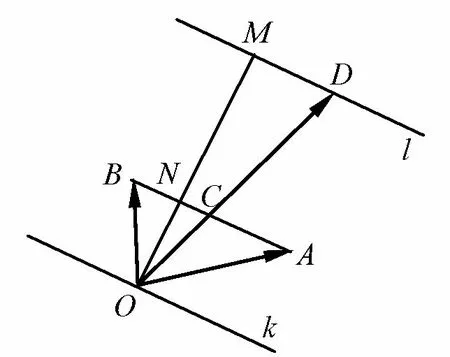
图10
学生10:比值让我联想到了平行线,过P作AB的平行线l,过O作l的垂线分别交AB,l于M,N,x+y=λ=如何变化我还需要再思考下.
学生11:老师,我发现|ON|是个定值!
教师:对,所以呢?
学生11:|ON|不变,所以当l向右上平移,|OM|变长,从而λ变大.
教师:回答的非常好.
大家为学生11的精彩回答鼓掌,教师接着补充.
教师:由于|OM|的变长,当l从左下角向右上角平移的过程中,x+y是不断增大的.当P在直线k与直线AB之间,x+y的范围是多少? 当P在直线k上,x+y的值是多少? 当P在直线AB右上时,x+y的范围是多少?
学生12:当P在直线k与直线AB之间,|OM| ∈(0,|ON|),于是当P在直线k上,|OM=|ON|,于是当P在直线k与直线AB之间,于是
师生小结:即λ的值可用AB的平行线这把“尺度”来度量,在越远离起点O的平行线上,λ的值越大(这里暂时不考虑负值的情况),在同一条平行线上时λ的值不变.
教师:下面我们来看两道高考题,感受高考对这类问题的考察.
练习2(2009年高考安徽卷理科第14题)给定两个长度为1的平面向量它们的夹角为120°.图11所示,点C在以O为圆心的圆弧AB上变动.若其中x,y ∈R,则x+y的最大值是_____

图11

图12
解析
学生13:如图12,平移线段AB直至与圆弧AB相切,当C恰为切点时x+y最大,易得D为OC中点,OC= 2OD,x=y的最大值
练习3(2017年高考全国ⅠⅠⅠ卷理科第12题)在矩形ABCD中,AB= 1,AD=2,动点P在以点C为圆心且与BD相切的圆上.则λ+μ的最大值为().


图13
学生14:如图13,平移线段BD直至与圆C相切,当P恰为切点时λ+μ最大,过A作AM垂直MP于M点,易得MN=EP= 2r,AN=CE=r,于是λ+μ的最大值
4 总结反思 任务后续
教师:最后我们来总结这节课的收获.
学生15:用共线定理的推论整体求出系数和.
学生16:用平行线作为尺度,判断系数和的最值.
教师:课后请大家思考两个探究.
探究1P是正方形ABCDEF某一边上的一点,则x+y的最大值为()
A.4 B.5 C.6 D.7
探究2(变式)如图14,在正方形ABCD中,E为AB中点,P为以A为圆心、AB为半径的圆弧上的任意一点,设向量则λ+μ的最小值是___
解析本题需要把向量平移到同一个起点,如图15,将DE平移到AF,连接PF交AC于点G,则当P从D转到B时G在右移,AG在变长,所以当P在B处λ+μ值最小,由中位线易得最小值是

图14

图15
章建跃先生认为:“从数学知识发生发展过程的合理性、学生思维过程的合理性上加强思考,这是落实数学学科核心素养的关键点”[1].作为教师,不光要讲推理,更要讲道理,把数学知识转化为学生容易接受的教育形态.为此,这节课的设计我注重让学生自己发现,自主探究,理清知识的来龙去脉,学生有困难的地方注重衔接,用问题串的形式层层递进,层层深入,问题串之间又设问让过度做到自然平缓,如在整体求x+y时,让学生联想哪里有系数和,从而想到用共线定理推论,求x+y最大值时,因为有比例式,让学生联想到了平行线,以期用一个个小问题,激发学生的思维.这节课上完后,我也发现了自己的一些不足之处:学生是学习的主体,在今后的教学中我还应给予他们更多的宽容.把学习的主动权交给学生,把提问的权利交给学生,把讲解的机会让给学生,促进更加主动的探究知识,在探究中提升逻辑推理能力.另外对细节的把握上,还不能做到放缩自如,老师要给学生一杯水,老师自己就要有一缸水,一潭水,一节好的课,绝不是靠暂时的努力就能做到的,罗马不是一天建成的,只有不断积淀,提高自身素养,“腹有诗书气自华”,课堂上才能做到“随风潜入夜,润物细无声”.

