解析基本图形 树立模型意识—-一道三角形全等问题的教学反思
广东省东莞市常平中学初中部
基本图形一般是指在教材中描述图形定义、公理、定理的图形,以及一些具有代表性的例题和习题中的图形.解析基本图形,能够帮助学生快速找到几何综合题的解题突破口,攻破教学难点,提升解题效率,发展学生的几何直观和逻辑推理能力.
1 提出问题
1.1 题目呈现
问题1如图1,正方形ABCD中,E是对角线BD上一点,连接CE,过点E作EF⊥CE交AB于点F,求证:EF =EC.

图1
这是八年级下册《平行四边形》期末复习中的一道练习题,在规定时间里全班48名学生仅有3人成功解答.其实本题的证明过程不算复杂,只要学生对正方形的轴对称性有一定的感知,对此前学习正方形的性质时解决过的一些基本图形有所印象,比较容易想到的是添加一条辅助线构造一对轴对称的全等基本图形的解题思路,如图2,图3.

图2

图3
以图2为例,连接AE,易证ΔABE∽= ΔCBE(或ΔDEA∽= ΔDEC),得到EA=EC,∠1=∠2,然后由四边形EFBC内角和得出∠4+∠3 = 180°,再转化出∠1 = ∠3,进而EA=EF,最后等量代换证得EF=EC.
1.2 障碍分析
通过交流发现,最初多数学生陷入了证明“ΔBFE∽= ΔDEC”的误区,找不齐全等的条件,一部分学生想到了添加辅助线,尝试“连接FC,然后努力证等角对等边”,朝这两个方向努力的学生都感到条件“EF⊥EC”难以利用.说明学生对这类需要添加辅助线构造全等三角形的问题缺乏解题经验,对题目中隐含的基本图形(如图4,图5)表征的识别存在较大困难,无法利用过往经验,造成解题效率低下.

图4

图5
2 利用基本图形分析法的解题教学
解析基本图形是中考压轴几何综合题的重要解题技巧,为此笔者设计了一节添加辅助线,构造三角形全等基本图形的几何证明习题课,旨在帮助学生掌握解析基本图形的解题方法,形成转化核心模型的解题意识.
2.1 三角形全等的基本图形应用举例
习题课围绕两类三角形全等的基本图形展开,第一类采用启发引导,第二类采用探究发现的方式.
题组1
(1)如图6,已知AB//CD,点O是BD的中点,求证:ΔABO∽= ΔCDO.
(2)如图7,ΔABC中,AB=AC,E是AC延长线上的一点,D是AB上一点,且CE=BD,连接DE,交BC于点F,求证:DF=EF.

图6

图7
题组2
(1)如图8,AB=AC,AD平分∠BAC,求证:ΔABD∽= ΔACD.
(2)如图9,ΔABC中,AD是角平分线,∠ABD=2∠C,求证:AC=AB+BD.

图8

图9
题组1的教学中,多数学生一开始未能发现图6就是隐含在图7中的基本图形,通过引导学生观察图7中有无图6的若干表征,一些学生终于懂得围绕着以F点为顶点的一对对顶角构造8 字全等形,通过合作交流,学生们又找出了几种不同的做法,如图10,过点D作AE的平行线,或者如图11,过E点作AB的平行线,然后证一个小的等腰三角形和一对8 字形全等,也可以如图12,分别过点D,点E作BC的垂线段,然后证两次全等.

图10

图11

图12
题组2的教学中,学生懂得了在图9中找寻图8的表征,约有三分之一的学生在规定时间里找到了添加辅助线构造图8这种对折全等形的办法,如图13,图14.

图13

图14
两个题组学完后,要求学生总结反思,在图形中具有怎样的表征时,可以尝试构造8 字全等形,具有怎样的表征时,可以尝试构造对折全等形? 多数学生能够发现前者的表征包含有:平行线段,对顶角,后者的表征包含有:角平分线,公共边,有4位同学还观察到了图7中隐含有平行四边形对角线互相平分的模型.
2.2 教学效果检测
题组3
(1)如图15,B是AC上一点,分别以AB,BC为边在AC同侧作等边ΔABD和等边ΔBCE,连接DC,AE,求证:DC=AE.
(2)如图16,D是等边ΔABC外一点,连接BD,CD,AD,∠BDC=120°,求证:AD=BD+CD.

图15

图16
题组3中的第一题是之前学过的很熟悉的一道练习,这里仅仅是出示给学生们温习一下不需要再次解答,但是要求学生描出图15中隐含的基本全等图形,在规定时间里,全班有27名学生(约占总数56%)想到了延长BD到E,连接CE,构造ΔBCE∽= ΔACD的办法,如图17,并能够成功抽取出一对旋转的全等模型,如图18.

图17

图18
3 反思与建议
数学家G·波利亚的《怎样解题》表中的精髓是启发学生懂得去联想,思考要解决的问题与过往早已解决的哪个问题有联系,能否加以利用? 在解需要添加辅助线的这类几何证明题时,能够识别图形中的若干表征,展开联想,构造出过往熟悉的基本图形,是提升解题效率的关键.
3.1 进行图形分解,识别基本图形
对图形进行分解,识别其中隐含的基本图形,甚至是多个基本图形,是解决中考压轴的几何综合题的重要方法.近年来一些中考教研活动中,多位名师分享的中考中求解圆的综合题的经验就是进行图形分解,还有的分享了利用Geogebra 软件对图形进行解析,也大大提高了解题的效率.
对于八年级的学生来说,解答问题1 之前,其实都具有分析图19,图20的经验,但从问题1的答题情况来看,学生对之前学过的熟知图形并未进行深度分解.

图19

图20
图19,图20中都含有图21,图22这样两个基本图形,而问题1中也含有图22这样一个基本图形,当很多学生感叹问题1中的条件“EF⊥EC”难以利用时,其实是对过往的图形缺乏深度分解与感知,否则还可以想到一种做法,就是过点E作EM⊥AB于点M,作EN⊥BC于点N,然后可以证明一个小正方形和一对全等的直角三角形,也能求解.

图21

图22

图23
3.2 展开表征联想,构造基本图形
有些题目,隐含着基本图形,但是图形不完整,难以直接分解,需要根据某些图形表征,展开联想,构造出基本图形.这就需要平时的教学中,引导学生加深对基本图形表征的认识,达到见微知著的效果.
问题2如图24,ΔABC中,AB= 6,AC= 10,AD平分∠BAC,BD⊥AD,点E是BC的中点,连接DE,求DE的长.

图24
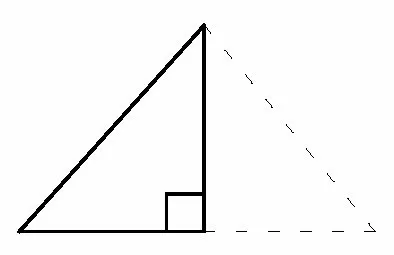
图25

图26

图27
在这道题目中,引导学生对图24中的角平分线,垂直和中点展开联想,进而能够想到三线合一的基本图形(如图25),三角形中位线的基本图形(如图26),两个基本图形都导向延长BD的辅助线方法(如图27).
3.3 树立模型意识,提升解题能力
数学教育家罗增儒教授提倡在学习数学的过程中,要善于对新问题展开联想,辨别它是否属于某个已经掌握的类型,如果不直接属于,那么能否进行一些变化,使之属于某个类型.在平面几何的学习过程中,要引导学生积累所学的基本图形,并把图形的表征、性质,以及构造的方法作为整体,进行加工提炼,得出有长久保存价值的图形模型和方法模型,建立模型库,在解决新问题时,方便及时提取应用,进而提升解题能力,发展数学核心素养.
问题3如图28,O是正方形ABCD内部一点,OB=求正方形的面积.
问题4如图29,O是等边ΔABC内部一点,OA=3,OB=4,OC=5,求∠AOB的度数.

图28

图29

图30

图31
问题3的计算是有一定难度的,但是学生如果对之前学习勾股定理逆定理时求解过的问题4 有印象,那么就可以类比那种方法,绕B点顺时针90°旋转构造一对全等三角形(如图30),利用勾股定理逆定理求出∠BPC的度数,然后再用两次勾股定理解ΔBPC(如图31),求出BC的长,即可求解.
4 结语
几何证明是初中数学的重点内容,也是一个难点,任何几何问题都是由基本图形构成的,在教学中我们要引导学生“一找,二用,三思考”.首先是会在复杂图形中找出基本图形,这就需要学生在日常的学习中重积累,能够抓住基本图形的本质与表征;二是会正确使用基本图形的性质,能够对图形中相关联的几何元素进行定性定量的分析与转换;三是会借助基本图形,发散思维,进行深度思考.思考基本图形有哪些常见的变化? 变化中有着怎样的规律? 不同的变化带来哪些不同的解题方法? 方法之间有无共性等.
初中数学课程目标之一,就是教学生学会思考,基本图形分析法的教学能够有效地教会学生如何思考解决几何问题,帮助学生发展直观想象和逻辑推理能力,树立模型意识,进而促进学生数学核心素养的发展.

