温稠密等离子体中Al12+离子的光电离过程

施蕾蕾，赵国鹏，祁月盈

（嘉兴学院数理与信息工程学院，嘉兴 314001）

1 引言

原子光电离过程能够反映原子中电子能级、波函数和电子间关联效应的微小变化，可以作为理解复杂物理系统结构的工具.对于孤立环境中原子和离子的光电离过程，已经开展了大量的理论和实验研究工作［1-3］.近几十年，随着天体物理、激光等离子体、惯性约束聚变等研究领域的快速发展，人们研究了等离子体环境对原子光电离过程的影响，发现与孤立环境中的纯库仑相互作用相比，等离子体屏蔽势的短程性会导致光电离截面表现出许多不同的特性.最显著的特性有离心势垒导致的势形共振［4］和初态波函数节点导致的Cooper极小［5］；在准束缚态存在时，可以在np→εs跃迁对应的截面中观察到虚态效应［6，7］；光电离截面的低能依然遵守Wigner阈值定律［8］.

对于弱耦合的经典等离子体，其中电子和离子间的相互作用可以用Debye-Hückel势进行描述，其形式为

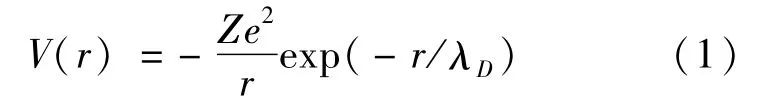
其中λD=（kBTe/4πe2ne）1/2是Debye屏蔽长度，Te和ne分别是等离子体的电子温度和密度，kB是玻尔兹曼常数，e为电子电量.势场（1）适用的条件是库仑耦合强度Γ=（4πe6ne/3）1/3/（kBTe）＜＜1的情况.目前大多数等离子体屏蔽效应对光电离过程影响的研究工作，大都集中在这种低密高温等离子体环境［6，9-16］.

当等离子体温度低于电子费米温度，而且等离子体中电子的德布罗意波长接近或大于平均粒子间距的强耦合等离子体（Γ＞1）时，采用离子球屏蔽模型研究其中的光电离过程［17，18］，这种模型适用于不考虑温度的稠密等离子体环境.还有一种由线性量子流体动力学理论得到的，适用于稠密等离子体环境但不包含温度的屏蔽势的形式为［19］

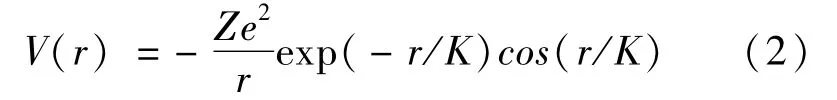
其中K=（ħ2/2πe2mene）1/4是屏蔽长度，ħ和me分别是约化普朗克常数和电子质量.已经有研究人员利用这种屏蔽势探究了量子等离子体中类氢离子的光电离过程［20，21］.需要指出的是等离子体的电子简并效应没有包含在屏蔽势（2）中.

2015 年Stanton和Murillo提出了一种新的屏蔽势［22］，既适用于高温低密度的经典德拜等离子体也适用于低温高密度的量子等离子体，这种屏蔽势还包含了等离子体简并效应，以及有限温度对动能的梯度修正和量子交换关联效应，在后文中表示为SM势.有限温度对动能的梯度修正和量子交换关联效应通过响应函数分别包含在参数中.当满足条件ν＜b2时，SM势表示为

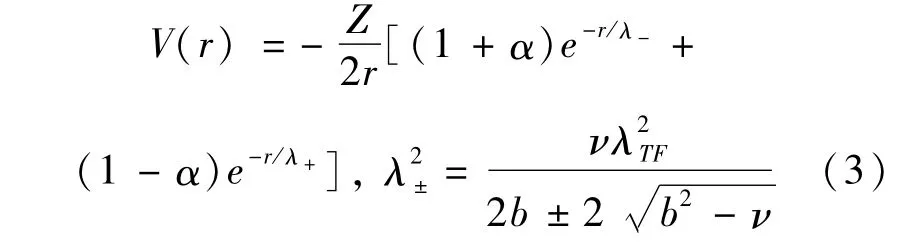
当满足条件ν ＞b2时，其形式为

图1 表征了SM势适用的温度和密度范围［23］，即曲线ν=b2上方和下方的区域分别适用于形式（3）和（4）.

图1 函数ν=b2在（ne，Te）坐标中的值［23］Fig.1 The function ν=b2 in the（ne，Te）space［23］.

本文在相对论理论框架下，采用SM势的形式（3）研究温稠密等离子体环境中类氢离子的光电离过程.以Al12+离子为例，固定等离子体标度温度，研究强耦合等离子体条件下（耦合强度接近或大于1）密度变化对能级、波函数和光电离截面的影响；作为比较，将同时给出同样的温度和密度条件下Debye-Hückel势的光电离截面，分析等离子体简并、有限温度对动能的梯度修正和量子交换关联效应对光电离过程的影响.需要指出的是，虽然相对论的光电离截面不能完全的标度化到任意类氢体系［15］，但是Al12+离子的计算结果能够体现所研究的等离子体环境效应的影响.除特别说明，本文后续内容都将采用原子单位.

2 计算方法

在相对论理论框架下，类氢离子的哈密顿量为

其中c是光速，α和β 是Dirac矩阵，p 是动量算符.径向波函数的大分量Pgκ（Z，λ±；r）和小分量Qgκ（Z，λ±；r）由Dirac耦合方程组确定.其中g=n或g=ε，分别对应束缚态的主量子数和连续态电子的动能，κ是相对论动量量子数.

采用标度变换［15］

方程（8）转化为标度形式

其中δnn'和δ（ε-ε'）是Kronecker符号.标度化的温度τe=Te/Z2［24］.

束缚和连续电子的Dirac态函数为

光电离截面的形式为

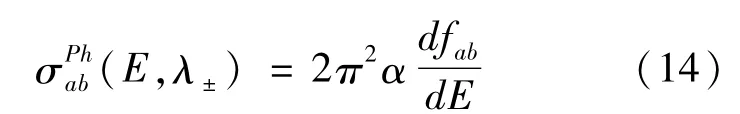
其中dfab/dE是初态和末态分别为束缚态a和连续态b的振子强度密度

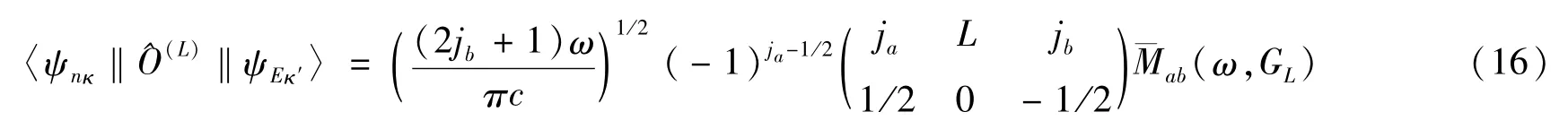
光电离截面（14）的标度形式为［15］

本文的计算中，我们分别采用修正的GRASP2K［27］和CONTWVSA［28］程序来确定相对论情况下的束缚和连续态波函数，采用WKB方法［29］对连续态波函数进行归一化.上述方法计算的能级和波函数的精度可以分别达到10-7和10-6.

3 计算结果与分析

图2 给出了等离子体的标度温度固定为τe=1.3 eV时，2lj和3lj态的标度能级随等离子体密度变化的关系.由图2（a）可以发现，随着电子密度的增大，nl态的简并被解除，且能级劈裂逐渐增大；同时，nlj态的能级随密度增大逐渐减小，直至达到密度临界值（对应一组特定的临界屏蔽长度和）时减小到零.存在这些特性是由于SM势的形式（3）在r→∞时，下降速度快于r-2［30］.图2（b）和（c）体现了相对论效应导致的nl态能级劈裂，对于相同的角量子数l，j较大时对应的束缚能较小.由图2（b）和（c）还可以分别看出，主量子数n和角量子数l越大时能级劈裂越小.

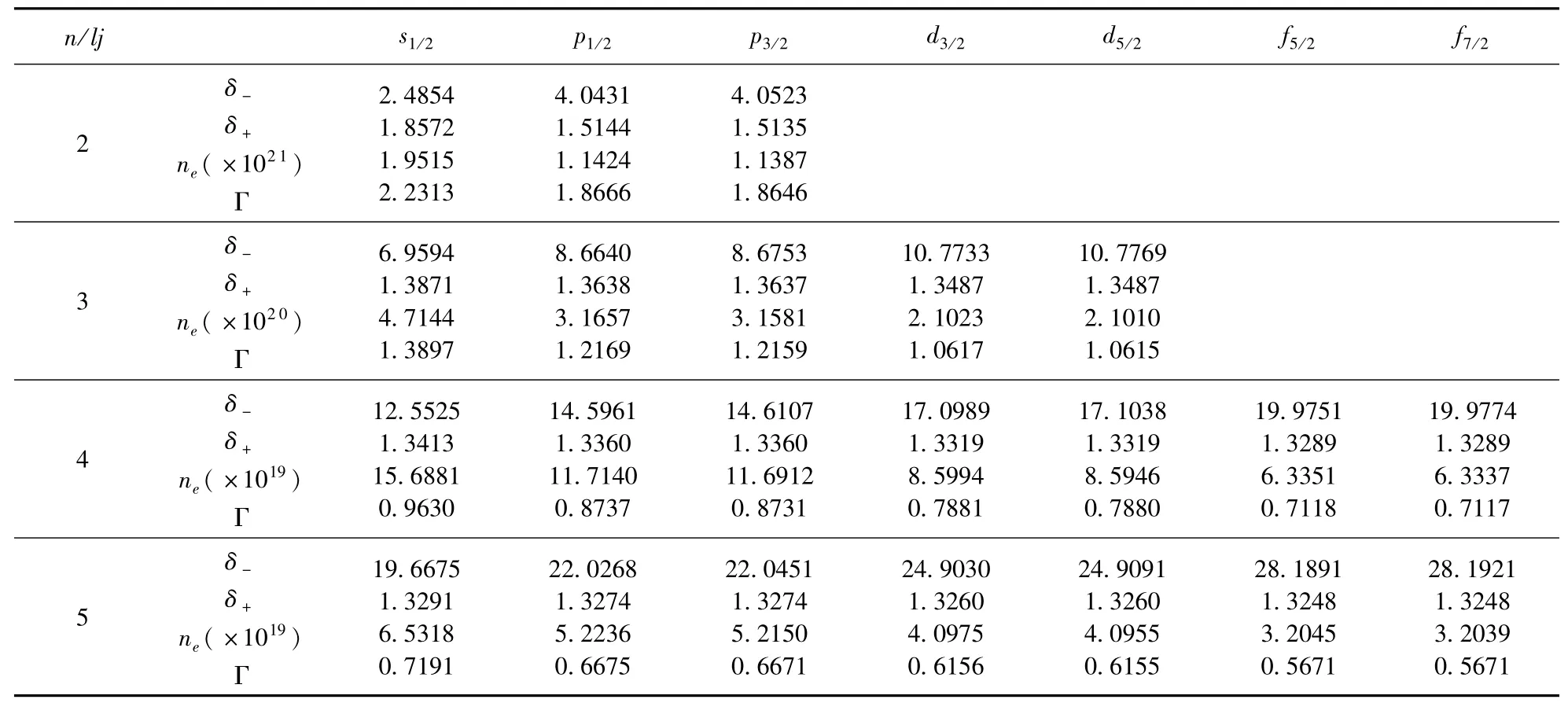
表1 固定标度温度τe=1.3 eV时，Al12+离子2≤n≤5的束缚态所对应的标度临界屏蔽长度，电子密度ne（cm-3）和库仑耦合参数Γ.Table 1 Scaled critical screening lengthsδ±，electron densities ne（cm-3）and Coulomb coupling parameterΓfor the Al12+states with 2≤n≤5，at the fixed scaled temperatureτe=1.3 eV.

表1 列出了等离子体的标度温度固定为τe=1.3 eV时，nlj（2≤n≤5）态对应的临界密度和临界屏蔽长度.从这个表格可以看出临界值对应的是强耦合等离子体环境（0.5671 ≤Γ≤2.2313），并且耦合强度随电子密度的增大而增强.等离子体的温度和密度参数处于这些临界值附近时，对应的连续态波函数和光电离截面将出现显著的变化，下面将着重进行分析.

图3 显示了标度温度和光电子能量分别固定为1.3 eV和0.00048 a.u.时，不同等离子体密度以及非屏蔽情况下εp1/2和εp3/2对应的连续态波函数随径向距离的变化关系.从该图可以看出，与非屏蔽情况相比，等离子体屏蔽效应使波函数发生了明显的变化，并且密度为ne=3.1576 ×1020cm-3和ne=3.166 ×1020cm-3时尤其显著（与图中其它情况相比，只有这两个密度值对应的εp1/2和εp3/2态的波函数可以分辨）.如表1 所示，这两个密度值非常接近3p1/2和3p3/2态的临界密度，其中3.1576 ×1020cm-3略小于3p3/2态对应的临界密度，3.166 ×1020cm-3略大于3p1/2态对应的临界密度.由图3 还可以发现，由于随等离子体密度增大，3p3/2比3p1/2先进入连续态，因此密度ne=3.1576×1020cm-3时，与εp1/2态相比，εp3/2态对应的连续态波函数振幅较大.然而，密度ne=3.166 ×1020cm-3时，却与密度ne=3.1576 ×1020cm-3的情况相反，即此时εp1/2态对应的连续态波函数出现了不同于一般情况的较大的振幅.出现这种现象的原因是由于此密度值略大于3p1/2态的临界密度，此时3p1/2态已经进入连续区域而成为准束缚态，电子可以被离心势垒暂时束缚在有效势的内部区域.反常增大的连续态波函数与对应束缚态之间的耦合矩阵元也将变得非常大，使得光电离截面中出现势形共振峰.

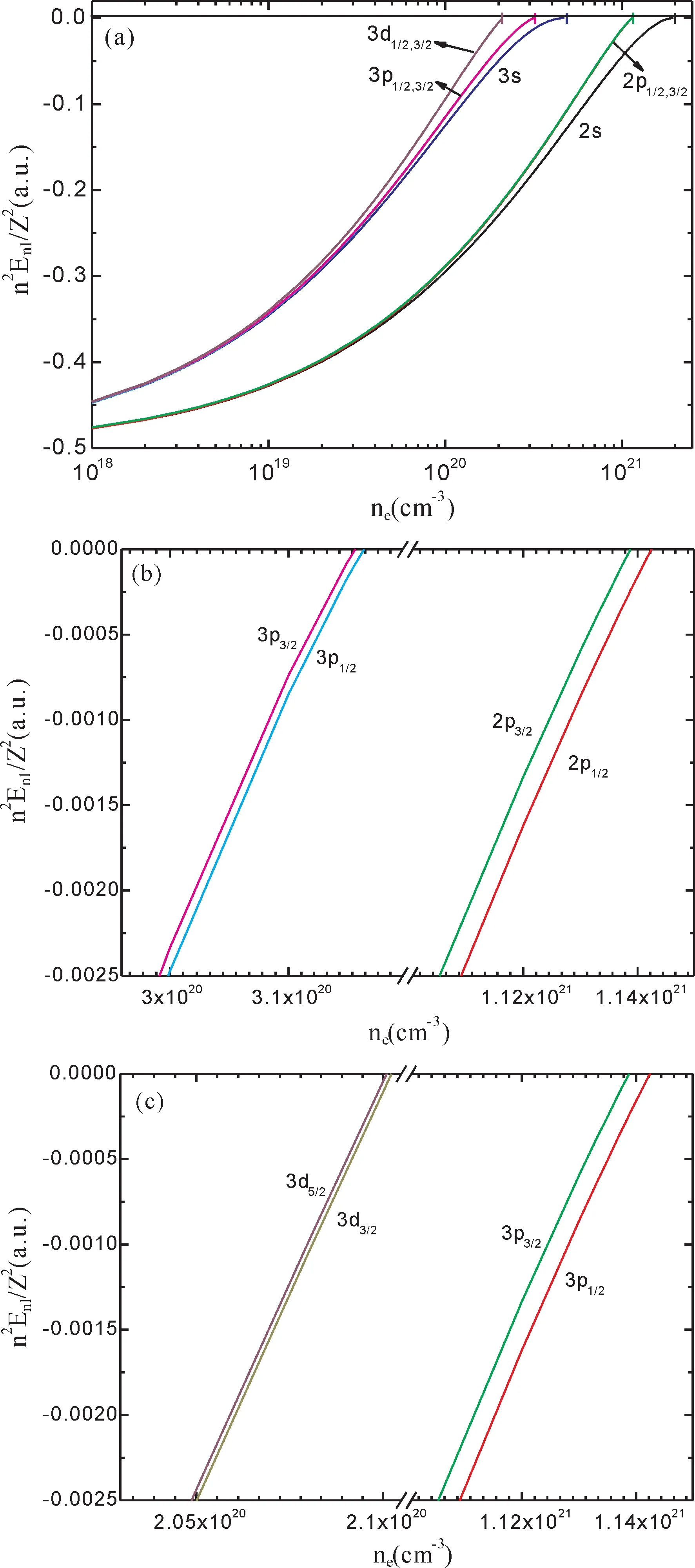
图2 （a）固定临界温度τe=1.3 eV时，Al12+离子 1s，2lj和3lj态的标度能级随电子密度的变化关系.（b）临界屏蔽密度附近2p1/2，2p3/2，3p1/2和3p3/2态的能量行为.（c）临界屏蔽密度附近3p1/2，3p3/2，3d3/2and 3d5/2态的能量行为.Fig.2 （a）Scaled energies of 1s，2ljand 3ljstates of Al12+ion as a function of electron densities with fixed scaled temperatureτe=1.3 eV.（b）Behavior of 2p1/2，2p3/2，3p1/2and 3p3/2energies near the critical screening lengths.（c）Behavior of 3p1/2，3p3/2，3d3/2and 3d5/2energies near the critical screening lengths.

图4 给出了标度温度和光电子能量分别固定为1.3 eV和0.0038 a.u.时εp1/2和εp3/2对应的连续态波函数相位随等离子体密度的变化关系.如图所示，所有相位发生π弧度变化的位置都处于某一个态的临界密度附近，即对应出现准束缚态的等离子体温度和密度参数，因此这些相位突变是光电离截面中能够出现势形共振的特征.图4（b）分别放大了2p1/2，3/2和3p1/2，3/2态临界密度附近的横坐标，该图可以看到相对论效应导致的两个非常接近的相位突变，这将在总光电离截面中表现为双共振现象.

为了研究温稠密等离子体环境效应对光电离过程的影响，我们分别采用SM势和Debye-Hückel势开展相同等离子体条件下Al12+离子光电离过程研究.在图5（a）和（b）中，我们分别给出了利用SM势（3）和Debye-Hückel势（1）计算的标度温度固定为τe=1.3 eV时，不同等离子体密度情况下Al12+离子1s态的光电离截面.由图5（a）可以看出，与非屏蔽情况（黑线）相比，等离子体屏蔽效应使光电离截面发生了很大的变化，尤其是当密度ne=3.1617 ×1020cm-3，3.166 ×1020cm-3，1.1397×1021cm-3和1.1437 ×1021cm-3时，由于其值接近3p1/2，3/2和2p1/2，3/2态的临界密度，出现了势形共振峰.密度ne=3.1576 ×1020cm-3时，虽然接近但是略小于3p3/2态的临界密度，不存在准束缚态，没有离心势垒束缚自由电子，因此对应的光电离截面中没有出现势形共振峰.对比4 个出现势形共振的情况可以发现，ne=3.166 ×1020cm-3和1.1437 ×1021cm-3时出现了双共振峰，而ne=3.1617 ×1020cm-3和1.1397 ×1021cm-3时仅有一个共振峰.这是由于3.166 ×1020cm-3和1.1437 ×1021cm-3分别略大于3p1/2，3/2和2p1/2，3/2态的临界密度，1s态分别跃迁到εp1/2和εp3/2态的光电离截面中都会出现势形共振，它们在总截面中的共同贡献即双共振峰，是相对论效应的体现.密度ne=3.1617 ×1020cm-3和1.1397 ×1021cm-3时分别略大于3p3/2和2p3/2态但小于3p1/2和2p1/2态的临界密度，只有1s态跃迁到εp3/2态的光电离截面中会出现势形共振.

图4 固定标度温度τe=1.3 eV和电子能量ε=0.0038 a.u.时，Al12+离子εp1/2（虚线）和εp3/2（实线）态标度的连续波函数的相位随等离子体电子密度的变化关系（a），以及相位在临界密度附近行为的放大（b）.Fig.4 Phase of continuum wave functionsεp1/2（dashed lines）and εp3/2（solid lines）for Al12+ion as function of electron densities for ε=0.0038 a.u.with fixed scaled temperatureτe=1.3 eV（panel（a）），and their expanded behavior near the critical screening lengths（panel（b））.

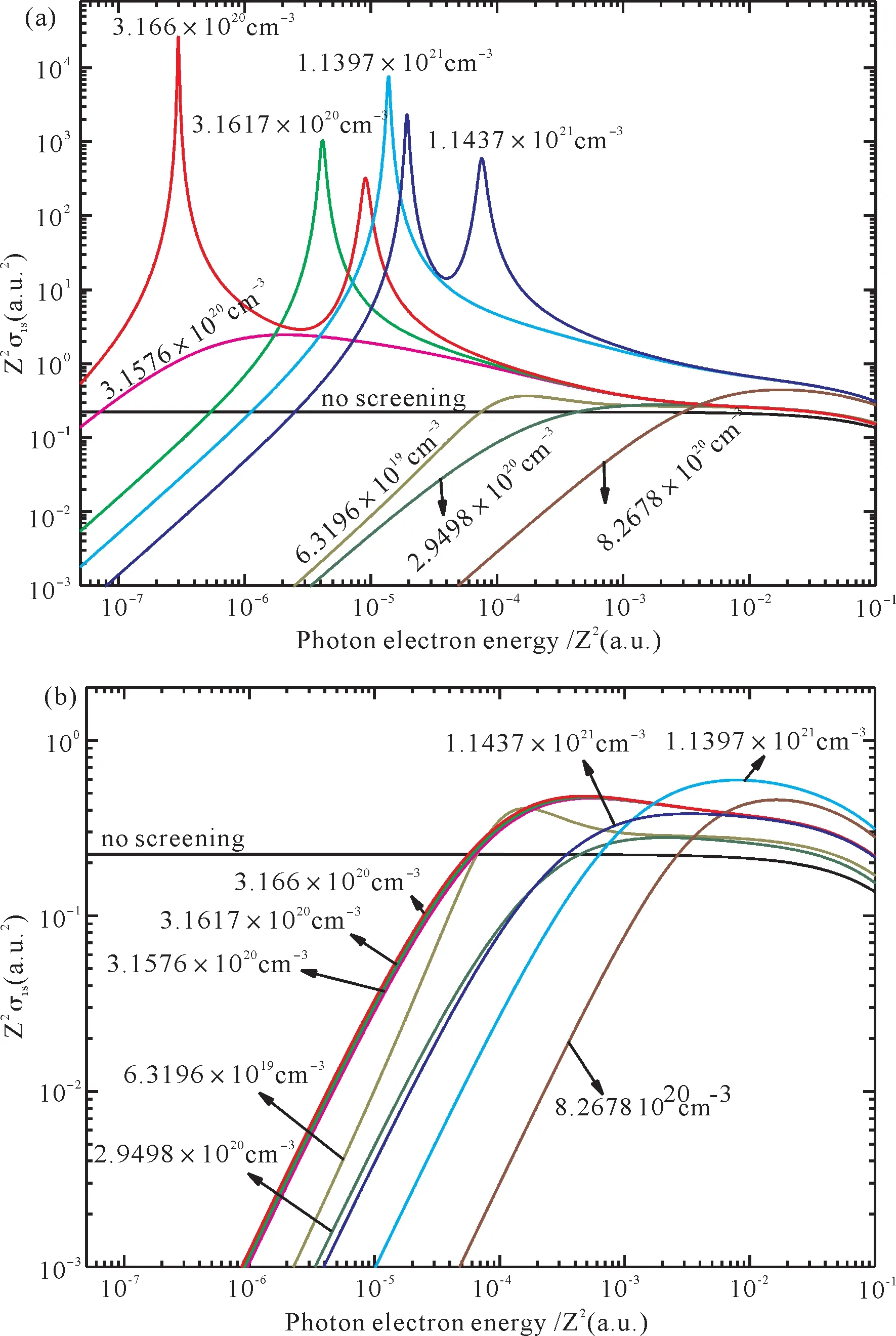
图5 固定标度温度τe=1.3 eV时，不同密度下分别利用（a）SM势和（b）Debye-Hückel势计算的Al12+离子1s态的总光电离截面随标度光电子能量的变化关系.（图中Z=13）Fig.5 Behavior of total 1s photoionization cross sections calculated by（a）potential（3）and（b）Debye-Hückel potential（1）of Al12+ion as a function of scaled photoelectron energy with fixed scaled temperatureτe=1.3 eV for different densities.（Z=13 in the figure）

对比图5（a）和（b）中相同等离子体参数所对应的光电离截面可以发现，密度ne=6.3196 ×1019cm-3，2.9498 ×1020cm-3和8.2678 ×1020cm-3时结果非常接近，然而对于其它接近3p1/2，3/2和2p1/2，3/2态临界密度的情况，截面大小和随光电子能量的变化趋势都有非常大的差异：图5（b）中没有出现势形共振峰.这说明与描述经典等离子体的Debye-Hückel势相比，SM势包含了等离子体简并效应、有限温度对动能的梯度修正和量子交换关联效应，因此修正了出现准束缚态时所对应的等离子体温度和密度条件.图5（a）中的共振峰可以认为是等离子体多体关联和量子交换关联效应作用的结果.

4 结论

本文采用多组态Dirac-Hartree-Fock方法和SM屏蔽势（包含了等离子体简并效应，有限温度对动能的梯度修正和量子交换关联效应），研究了温稠密等离子体环境中Al12+离子的光电离过程.我们计算了等离子体标度温度为1.3 eV时，不同等离子体密度情况下Al12+离子的能级，连续态波函数和光电离截面.结果表明，在能级减小到零的临界密度附近存在准束缚态，使连续态波函数的振幅反常增大，导致光电离截面中出现势形共振峰.而在同样的等离子体温度和密度条件下，利用Debye-Hückel势得到的光电离截面未出现势形共振峰，这是由于与SM模型相比，Debye-Hückel势没有充分考虑温稠密等离子体环境的多体效应，而光电离过程能够反映等离子体环境中关联效应的微小变化，并且在接近临界密度时以势形共振的形式表现出来.