硅(Si)原子高激发态能级自然辐射寿命的测量
王兴豪,于 启,耿一丹,戴振文
(1.东华理工大学理学院,南昌 330013;2.吉林大学物理学院,长春 130012)
1 引言
近年来,随着天文观测技术的不断发展,人们获得了大量高分辨率、高信噪比的天体光谱.对这些光谱进行化学元素丰度分析是探索银河系和其它星系形成和演化的基本途径.硅原子(Si,Z=14)是地壳中含量第二丰富的元素,并且在太阳和很多恒星的光球层吸收谱中也存在大量Si谱线,因此对Si化学元素丰度的分析一直是天文学家感兴趣的研究课题[1-5].原子和离子的振子强度数据是准确确定化学元素丰度的基本原子数据[6-8],而能级自然辐射寿命与分支比结合是确定振子强度实验值的可靠实验方法之一.
人们在Si原子能级寿命和分支比实验测量及理论计算方面已经做了一些工作.1966 年,Savage等人利用相移法测量了Si I 6 个能级的自然辐射寿命[9];1973 年,Marek和Richter利用相移法测量了Si I 3s23p4s3P谱项的自然辐射寿命[10];次年,Curtis和Smith用相移法测量了Si I 3s3p33D谱项的寿命[11];1980 年,Bashkin 等人利用束箔技术测量了Si I 3s23p4s1P、3s23p3d1P、3s23p3d1D、3s23p3d1F、3s23p4s3P和3s3p33D谱项的寿命值[12];同年,Becker等人利用激光选择激发方法测量了Si I 3s23p4s1P1、3s23p4s3P2和3s23p3d1P1态的寿命值[13];1989 年,Bergstrom等人通过激光两步激发测量了Si I 3s23p5p3S1、3s23p5p3P0,1,2和3s23p5p3D0,1,2能级的寿命值[14];1991年,O'Brian 和Lawler采用时间分辨激光诱导荧光(TR-LIF)技术测量了47 个Si I能级的自然辐射寿命[15];2002 年Coutinho和Trigueiros利用多组态Hartree-Fock(MCHF)方法计算了Si I偶宇称1s22s22p63s23p2,3s23p4p,3s23p5p,3s3p24s和3s3p23d组态以及奇宇称3s3p3,3s23pns(4 <n<22)和3s23pnd(3 <n <24)组态能级的寿命值[16];2005 年,Fischer利用Breit-Pauli近似方法计算了Si I 3s23p2,3s23p3,3s23p4s,3s3p3,3s23p3d 和3s23p4p 组态能级的辐射寿命[17];2008年,Liang等人采用多通道量子亏损理论计算了Si I 3pnd1F3(n=3~15)和3pnd3D3(n=3~18)里德堡系列能级的辐射寿命[18];2013 年,Ates和Ugurtan 采用弱束缚电子势模型和量子缺陷轨道理论计算了Si I 3s23p4s,3s23p4p,3s23p4p和3s23pnd(n=3,5~10)组态能级的辐射寿命[19].已有研究工作表明,Si I的现有辐射数据还很不完善,其较高激发态能级的辐射参数仍有许多工作要做.
鉴于此,我们采用TR-LIF技术结合激光诱导等离子体技术测量了Si I位于47351.55~63868.8 cm-1之间的14 个高激发态能级的自然辐射寿命,其中9 个能级的结果未见报道.
2 实验测量
我们基于TR-LIF技术测量能级寿命的实验装置如图1 所示.首先采用一台Nd:YAG激光器产生单脉冲能量5~20 mJ、重复频率10 Hz的纳秒激光脉冲,经透镜竖直方向聚焦至真空室中的旋转Si靶上,在激光烧蚀作用下,靶上方形成含有自由原子和不同价态离子的激光诱导等离子体.利用另一台Nd:YAG激光器产生波长532 nm、
重复频率10 Hz、脉宽约8 ns的激光脉冲泵浦染料激光器,产生可调谐激发光脉冲,经过一些非线性光学过程包括倍频、三倍频和拉曼频移等,将激发光调谐至实验所需波长.激发光经佩林布洛卡棱镜分光后导入真空系统,在靶上方6~8 mm处与等离子体中的Si原子作用,实现目标能级的选择性激发.Si原子被激发到目标能级后,由于自发发射会向下能级跃迁而发射荧光.荧光经凸透镜聚焦到单色仪中由光电倍增管探测,并输入示波器中进行采集、平均和存储.实验中,烧蚀激光、激发激光和荧光探测方向相互垂直.激发激光与烧蚀激光之间有一定的时间间隔,此间隔由数字延迟发生器(SRS DG535)控制.通过调节这个时间延迟,可避免等离子体复合发光对寿命测量的影响.

图1 寿命测量实验装置示意图Fig.1 Experimental setup for lifetime measurements
实验中,飞出视场、辐射陷阱、碰撞、超辐射、饱和以及量子拍等物理效应会严重影响测量结果的可靠性[20].飞出视场效应是指激发态原子发射荧光光子前飞出探测区导致测量结果偏短的现象;辐射陷阱效应是由于原子数密度过大,激发态原子数过多,其自发荧光被退激发后的原子再吸收而重新布居返回原激发态,导致寿命结果偏长;碰撞效应是指受激原子与周围粒子碰撞而去激发,引起测量结果偏短.超辐射效应指自发荧光过强而诱导受激原子的受激发射跃迁,导致寿命测量偏短;饱和效应是荧光强度过强致使探测系统出现非线性响应,导致测量结果偏长;量子拍效应是指地磁场所致塞曼分裂能级之间形成荧光干涉,在衰减曲线上叠加量子拍频振荡,引起信号失真.实验过程中,我们通过调节烧蚀激光与激发激光的强度以及它们之间的时间延迟,调节单色仪狭缝宽度,提高真空系统的真空度,施加强磁场等方法来消除这些效应的影响.
等离子体中原子速度和密度都会随烧蚀激光与激发激光间的延时而变化,因此可以通过观察寿命测量值在不同延时下的变化判断是否存在上述效应的影响.测量过程中,对每个能级,在不同激发-烧蚀脉冲延时下采集至少8 条荧光衰减曲线.图2 给出Si I 53387.33 cm-1能级在不同延时下测得的寿命值,可以看出寿命值在一定范围内涨落,说明测量过程中有效避免了各种效应的影响.
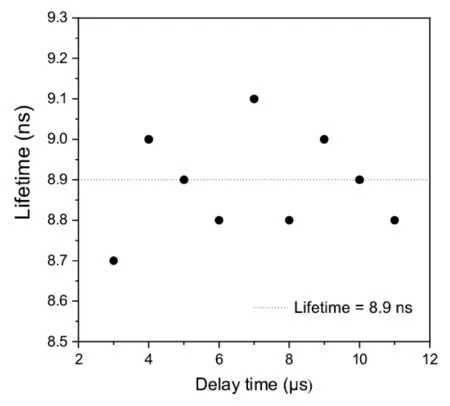
图2 53387.33 cm-1能级寿命测量值随激发-烧蚀激光之间延时的变化Fig.2 Lifetimes of the 53387.33 cm-1 level as a function of delay time between the excitation and ablation laser
3 结果与讨论
本文测量了Si I位于47351.55~63844.65 cm-1之间14 个能级的自然辐射寿命.当寿命大于40 ns时,采用e指数拟合荧光衰减曲线来确定寿命值.寿命值小于40 ns时,为了避免激发光脉宽的影响,需用激发脉冲和e指数函数对荧光曲线做卷积拟合来确定寿命值.图3 和图4 分别为Si I 61881.6 和53387.33 cm-1能级的荧光衰减曲线及其各自适用拟合方式下曲线拟合示意图.
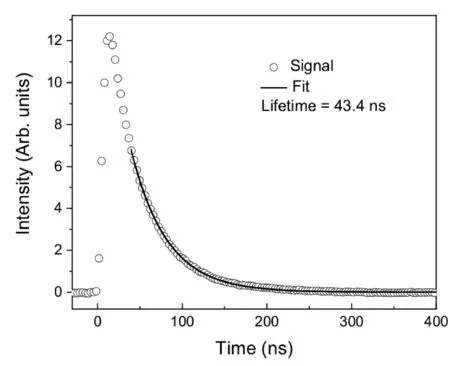
图3 61881.6 cm-1能级荧光衰减曲线的e指数拟合Fig.3 Typical fluorescence decay curve of the 61881.6 cm-1 level with an exponential fit for lifetime evaluation
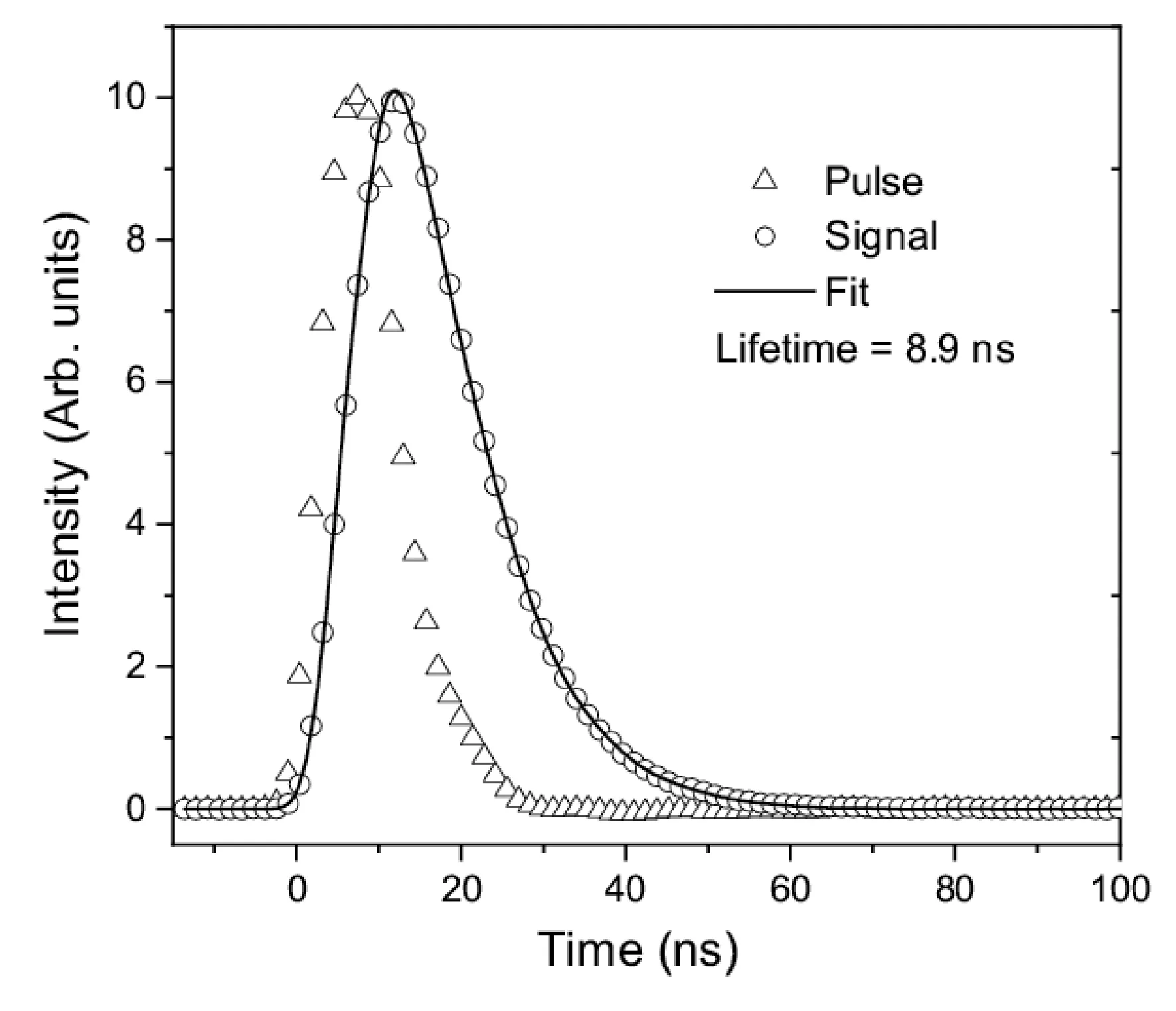
图4 53387.33 cm-1能级荧光衰减曲线的卷积拟合Fig.4 Typical fluorescence decay curve of the 53387.33 cm-1 level with a fitted convolution curve between the laser pulse and an exponential
表1 列出我们测得的14 个Si I能级寿命值,寿命结果分布在8.7~43.4 ns之间,误差均在10%以内.寿命测量误差包括散射误差和系统误差[20].为了验证可靠性和便于比较,前人实验测量结果和理论计算结果也列于表1 中.可以看出,对于实验结果,除59636.667 cm-1能级外,其它四个能级与前人结果在误差范围内符合很好,以本文结果为参考,差别在-2.7~7.9%之间.对于59636.667 cm-1能级,我们结果比O'Brian 等人[15]结果偏长30.8%.在寿命测量准确性的影响因素中,辐射陷阱和饱和效应会导致测量结果偏长.我们通过降低烧蚀和激发光能量、增大烧蚀与激发激光间的延时、降低光电倍增管电压、减小单色仪狭缝等操作反复对此能级的寿命进行测量,结果均在28.9 ns附近,所以可以排除这两种效应的影响.因此我们认为O'Brian 等人的实验过程中可能受到导致寿命偏短效应的影响.
对于本文首次测量的九个能级中,Coutinho等人[16]和Ate等人[19]对其中四个能级的寿命进行了理论计算.对比发现,仅有Coutinho等人使用MCHF方法计算的63844.65 cm-1能级和Ates等人使用弱束缚电子势模型计算的63097.36 cm-1能级的寿命结果与本文的测量结果符合较好,其它能级偏差较大.

表1 Si I能级寿命测量值及其与前人结果的比较Table 1 Measured lifetimes of Si I levels and comparison with previous results
4 结论
本文采用TR-LIF技术测量了14 个Si I高激发态能级(47351.55~63844.65 cm-1)的自然辐射寿命,其中九个能级属于首次报道.寿命值范围为8.7~43.4 ns,测量误差在10%以内.本文结果在一定程度上弥补了硅原子高激发态能级辐射参数实验数据的缺乏,它们对进一步确定能级跃迁几率和振子强度有重要意义.

