空间波函数的对称性对氦原子双光子双电离过程中电子关联的影响

李 飞，魏志义，王兵兵

（中国科学院物理研究所光物理重点实验室，北京 100190）

1 引言

电子关联普遍存在于化学、原子与分子物理和凝聚态物理领域中，对它的深入理解和操控有助于更全面地认识和控制原子或分子系统的动力学过程，例如化学键的形成与断裂、相变、超导等［1-3］.随着超短脉冲激光技术的发展［4-6］，人们可以利用超短脉冲探究与电子关联相关的超快现象，例如，电子关联导致镍在飞秒量级时间尺度上的退磁化过程［7］，电子关联也会引起氦原子光电效应过程中出射的光电子发生6 阿秒左右的延迟现象［3］等.氦原子的双电离是最简单的多电子动力学过程之一，因此被广泛地用于研究电子关联［8-10］效应的相关问题.

基于量子力学原理，一个全同粒子体系的波函数必须反映粒子之间不能被区分的要求，这意味着任何两个粒子状态的交换都不能改变体系的概率密度.因此，在交换粒子时要求体系波函数不是对称的就是反对称的.对称波函数的粒子被称为玻色子，而反对称波函数的粒子被称为费米子.由于电子属于费米子，因此氦原子核外两电子的波函数是反对称的.当氦原子处于单重态时，由于两电子的自旋波函数是反对称的，因此它们的空间波函数就是对称的；然而，当氦原子处于三重态时，由于两电子的自旋波函数是对称的，因此它们的空间波函数就是反对称的.近年来，人们对于氦原子单重态和三重态的研究主要涉及双电离电子的能量分布和角分布［11］，双电离截面与单电离截面的比率［12］，双电离的总截面和微分截面［13］，双激发态引起的共振增强［14，15］等，这些研究都是在长激光脉冲下的结果.在本文中我们要探究的问题是：空间波函数的对称性是否会影响氦原子在超短激光脉冲中的双光子双电离过程？基于之前关于氦原子双光子双电离过程中特征时间的研究［16］，本文主要从两个电离电子最终能量分配的角度探究空间波函数的对称性对电子关联的影响.

2 理论方法

我们采用数值求解含时薛定谔方程的方法研究激光脉冲与氦原子的相互作用.无外场下氦原子的薛定谔方程可以表示为（如果没有特殊说明，以下均采用原子单位）

体系的哈密顿量为

这里氦原子的核电荷数Z=2.根据变分原理，选择如下的试探波函数

就可以得到方程（1）中的本征波函数Ψn（r1，r2）.在（3）式中，P12是关于电子1 和电子2 的置换算符，是k阶B样条函数［17，18］，〈lαmαlβmβ|LM〉是Clebsch-Gordan系数，和是球谐函数，S、L 和M分别是两电子的总自旋，两电子的总轨道角动量和它的z分量.

在长度规范和电偶极近似下，含时薛定谔方程可以表示为

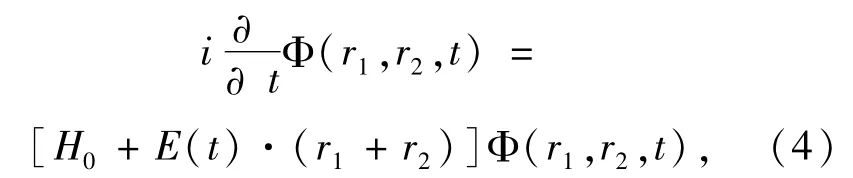
这里E（t）表示激光脉冲的电场分量.在我们的数值模拟中，选择如下形式的激光脉冲矢势

其相应的电场分量为

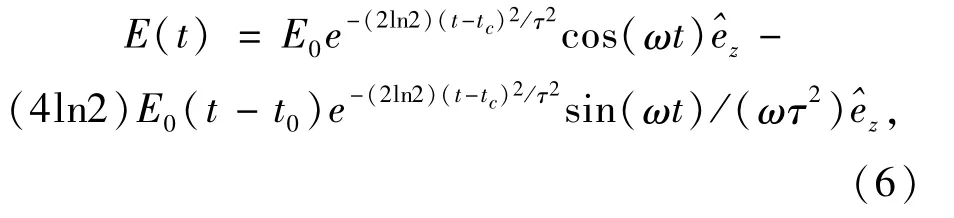
这里，E0=A0ω是电场的振幅，tc是激光脉冲在时间轴上的中心位置，τ是激光脉冲的半高全宽，ω是激光脉冲的载波频率，^ez是激光脉冲偏振方向的单位矢量.两电子的含时波函数可以用无外场下氦原子的本征波函数展开，即

将（7）式代入（4）式，可以得到一个耦合的微分方程，利用Admas方法求解上述微分方程组［19］，就可以得到含时波函数Φ（r1，r2，t）.一旦获得含时波函数，在投影时刻tf以动量k1和k2出射的两个电离电子的概率分布为

这里，ψk1，k2（r1，r2）是无关联的双电子连续态，它可以用两个独立粒子库仑波函数［20］的乘积表示，即

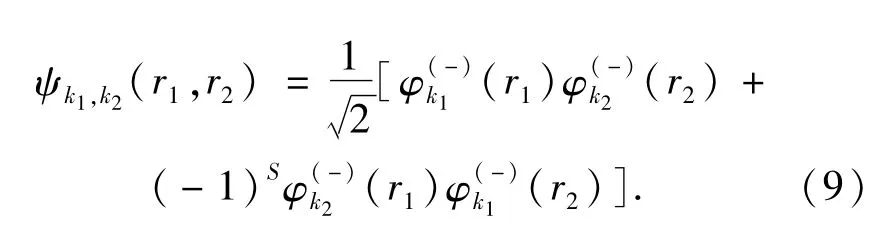
因此，两个电离电子的能量分布可以表示为

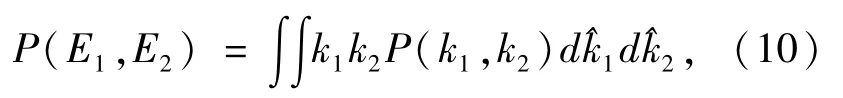
3 结果与讨论

我们通过比较相同激光脉冲作用下氦原子单重态1s2s1S 和三重态1s2s3S 的双光子双电离过程，研究空间波函数的对称性对电子关联的影响.表1 给出了氦原子单重态1s2s1S和三重态1s2s3S的能量以及库仑相互作用能=〈Ψn（r1，r2）|1/|r1-r2||Ψn（r1，r2）〉［11］数值的比较，这里的库仑相互作用能在一定程度上反映了处于氦原子定态的两个电子之间电子关联的强弱，可以看出单重态1s2s1S 和三重态1s2s3S 的能量之差和库仑相互作用能之差都小于0.03 a.u.，这表明上述两个态的电离能和电子关联的差异是微小的.

表1 氦原子单重态与三重态的能量以及库仑相互作用能的比较Table 1 Comparison of energy and Coulomb interaction energy for the singlet state and the triplet state of helium atom

首先，我们研究强度为1 ×1014W/cm2，载波频率为2.1 a.u.的激光脉冲与氦原子单重态1s2s1S作用下的双光子双电离过程.如图1（a）所示，当激光脉冲的持续时间为50 as时，两个电离电子能量分布呈现关于直线E1=E2对称的单峰，这里的单峰意味着两个电离电子大体上携带相等的能量.然而，当激光脉冲的持续时间由50 as增加到80 as时，如图1 所示，两个电离电子的能量分布由关于直线E1=E2对称的单峰变为关于直线E1=E2对称的双峰，这里的双峰意味着两个电离电子大体上携带不相等的能量.

接下来，我们研究强度为1 ×1014W/cm2，载波频率为2.1 a.u.的激光脉冲与氦原子三重态1s2s3S 作用下的双光子双电离过程.如图2 所示，当激光脉冲的持续时间由50 as增加到80 as时，两个电离电子的能量分布总是呈现关于直线E1=E2对称的双峰，即两个电离电子总是携带不等的能量.

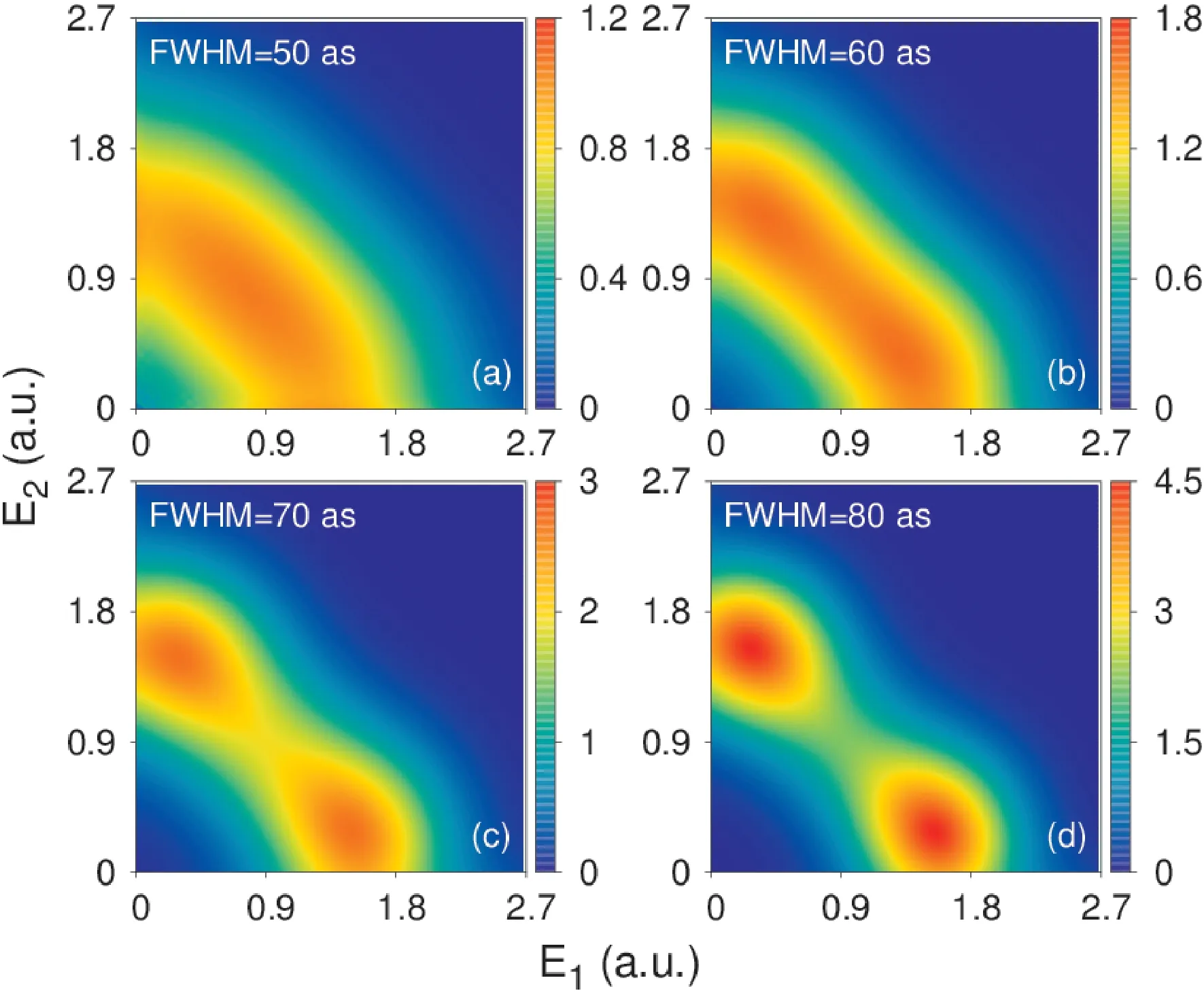
图1 两个电离电子的能量分布.双光子双电离过程的初态为1s2s 1 S态.高斯型激光脉冲的峰值强度为1 ×1014 W/cm2，载波频率为2.1 a.u.，脉冲持续时间分别为50 as、60 as、70 as、80 as.图中颜色棒的单位是10-8.Fig.1 Energy distribution of two ionized electrons.The initial state is 1s2s 1 S for the process of two-photon double ionization.The laser pulse has a Gaussian envelope with the peak intensity 1 ×1014 W/cm2 and carrier frequency of 2.1 a.u..The pulse duration（FWHM）is 50 as，60 as，70 as，and 80 as，respectively.The color bars are in units of 10-8.

比较图1 和图2 所对应的动力学过程，由于作用的激光脉冲是相同的，因此两个电离电子的能量分布随脉冲持续时间变化的差异来源于动力学过程的初态.对于氦原子的单重态1s2s1S和三重态1s2s3S，它们最明显的差异是前者的空间波函数是对称的，两个电子可以处在相同的空间位置，而后者的空间波函数是反对称的，两个电子不能处在相同的空间位置.更重要的是激光脉冲不会改变这两个态的上述差异，换言之，该差异会贯穿于整个动力学过程.基于两电子的径向电子密度分布，处于氦原子单重态1s2s1S和三重态1s2s3S上的两个电子都是一个电子离原子核较近，而另一个电子离原子核较远，即一个电子携带较低的能量，而另一个电子携带较高的能量.对于图1（a）所对应的初态为单重态1s2s1S的双光子双电离过程，初态的两个电子携带不相等的能量，在超短激光脉冲的作用下每个电子各自吸收一个光子而被电离，而最后出射的两个电子却携带大体相等的能量，这意味着在非常短的相互作用时间内两个电子通过电子关联传递了能量.当增加激光脉冲的持续时间时，如图1（b -d）所示，最后出射的两个电子逐渐明显地携带不相等的能量，这意味着两个电子通过电子关联传递能量的过程被抑制的.然而，对于初态为三重态1s2s3S的双光子双电离过程，如图2（a）所示，在非常短的相互作用时间内没有明显地观察到两个电子通过电子关联传递了能量.这些结果表明空间波函数的对称性的确影响了氦原子双光子双电离过程中的电子关联，至于具体物理图像，我们会在接下来的工作中去进一步的研究.

图2 两个电离电子的能量分布.双光子双电离过程的初态为1s2s 3 S态.高斯型激光脉冲的峰值强度为1 ×1014 W/cm2，载波频率为2.1 a.u.，脉冲持续时间分别为50 as、60 as、70 as、80 as.图中颜色棒的单位是10-8.Fig.2 Energy distribution of two ionized electrons.The initial state is 1s2s 3 S for the process of twophoton double ionization.The laser pulse has a Gaussian envelope with the peak intensity 1 ×1014 W/cm2 and carrier frequency of 2.1 a.u..The pulse duration（FWHM）is 50 as，60 as，70 as，and 80 as，respectively.The color bars are in units of 10-8.

4 结论

本文通过数值求解含时薛定谔方程，比较研究了氦原子的单重态1s2s1S 和三重态1s2s3S 作为初态的双光子双电离过程，发现在非常短的相互作用时间内，空间波函数的对称性会影响氦原子双光子双电离过程中的电子关联，最终导致两个电离电子的能量分布呈现不同的结构.