高电荷态类锂等电子序列（Z=31～40）1s2 2p态能级结构的理论计算

胡木宏，刘博文，徐恩慧，马玉龙，吴 勇

（1.辽宁师范大学物理与电子技术学院，大连 116029；2.北京应用物理与计算数学研究所，北京 100094）

1 引言

高电荷态离子体系的能级结构是原子物理研究的重要内容，这种特殊的离子体系具有不同于中性原子或较低电荷态离子的性质［1，2］，例如离子U91+的波函数在空间尺度上比中性氢原子缩小了约100 倍，这意味着中性原子物理性质的经验性诊断不再适用.高电荷态离子波函数向近核区域收缩的行为显著地改变了决定体系结构和性质的各种物理效应的相对重要性，体系角动量耦合图像逐渐偏离LS 耦合而向JJ耦合方向转变，人们所熟知的跃迁选择定则失效：总自旋量子数改变（即ΔS≠0），电偶极跃迁也可能发生；甚至总轨道角动量量子数改变（ΔL=0，±1），对L=0到L=1 的跃迁限制也可能被释放.另外，对高电荷离子体系的能级结构进行研究不仅可以揭示体系内部的基本物理规律，还可以为激光物理、等离子体物理、天体物理等相关领域提供高精度的光谱数据［3］，例如，星系团中存在大量的高电荷态离子，通过分析这些高电荷态离子的光谱可以了解星团中元素的种类和丰度，推演星体的年龄和形态.

近年来，以研究光电离和电子碰撞电离为主要机制的实验装置的搭建，为高电荷态离子的研究提供了实验平台，也为探知宇宙以及高电荷态离子的重要应用提供了可能［4］，但是关于高电荷态离子能级结构的实验数据甚少，已有的实验数据在精度上需要论证，在很多情况下需要高精度的理论结果进行评估.对于单电子体系而言，由于结构简单，比较容易实现能级结构的精确计算，文献［4］及其中引述的其他文献系统地总结了高电荷态类氢体系能级结构的理论计算成果.而多电子体系内部物理作用复杂，相对论效应、量子电动力学（QED）效应以及电子间关联效应影响显著，实现具体的高精度理论计算存在一定的难度［5］.在现有的理论研究中，非相对论的MCHF（Multi-Configuration Hartree-Fork）方法是实现多电子体系能级结构计算的有效方法之一.在这种方法中，基于N个独立电子波函数通过自洽场方法求解多组态Hartree-Fork 方程，得到一组计算原子能级结构的基，在此基础上加入组态相互作用，相对论效应、Breit修正和QED修正则通过微扰法进行处理.这种方法的优越之处在于有效考虑组态相互作用，构造的波函数能够充分地描述电子关联效应.MCDF（Multi-Configuration Dirac-Fork）方法是MCHF方法的相对论形式，其电子态波函数是具有相同对称性的多电子组态波函数的线性组合，包括了相对论效应，同时还系统地考虑了电子之间的关联效应，因此所得到的计算结果比较精确，为多电子体系结构和性质的研究提供了理论支持［6-10］.目前，F.Fischer小组和I.P.Grant小组根据MCDF方法的研究特点，合作研发了GRASP程序，为实现多电子体系能级结构的理论计算提供了直接有效的运行程序［11-13］.

具有1s2nl壳层结构的类锂体系是可以提供原子实、价电子以及价电子-原子实相互作用的简单体系，长期以来一直作为来衡量各种理论方法优劣的测试系统［14-17］.对于高电荷态类锂体系，随着核电荷数的增大，相对论效应、QED效应、原子核效应的影响逐渐显著，因此，固定电子数N研究具有不同核电荷Z的体系，即沿着等电子序列进行系统地研究，更易于揭示高电荷态离子的能级结构和性质的标度规律—随核电荷数Z增大而变化的定量规律.

本文以高电荷态类锂离子为研究对象，利用基于MCDF理论方法的相对论原子结构计算程序包GRASP2K，通过细致考虑电子关联效应构建准确可靠的体系波函数，完成对高电荷态类锂等电子序列22P激发态的能级结构和径向电荷密度的高精度理论计算.

2 理论方法

在相对论理论框架下，N-电子原子（离子）中单电子轨道波函数解析表达式为：

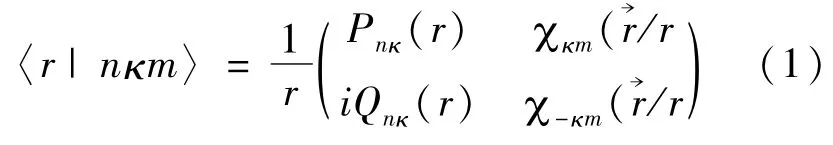
其中κ=±（j+1/2）是相对论角动量量子数，Pnκ（r），Qnκ（r）分别是径向波函数的大小分量，是旋量球谐函数：

将N个单电子原子轨道波函数的乘积进行反对称化和适当的角动量耦合后得到组态波函数|γPJM〉，再将具有相同的宇称、总角动量和总角动量分量的组态波函数进行线性组合，得到原子态波函数：

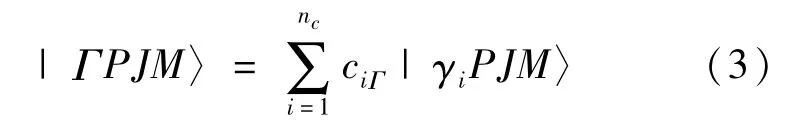
对于任意壳层i，电子径向波函数满足耦合的Dirac方程：

其中，Yi（r）是直接势能函数，与径向波函数有关；和是包含交换势贡献的非齐次项；εi是能量本征值.选取合适的组态和试探能级，运用多组态自洽法进行数值求解后确定单电子波函数基组；然后，固定所有单电子轨道波函数，选取适当的组态进行相对论组态相互作用计算（Relativistic Configuration Interaction，RCI），就能得到准确可靠的多组态原子态波函数.

在Coulomb规范下，N-电子原子（离子）体系包含纵向相互作用的哈密顿量为：

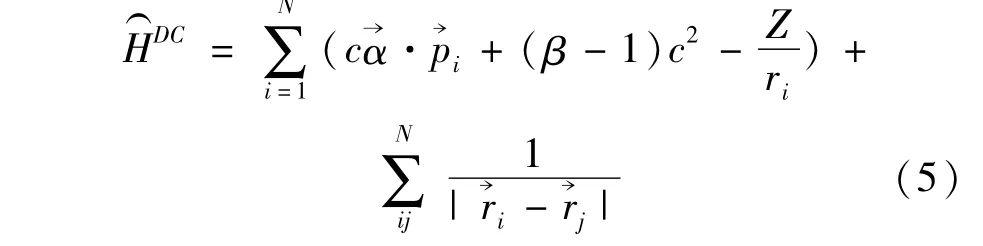
根据确定好的波函数，利用变分法进行能级结构的理论计算，哈密顿量HDC在原子态的期待值为：

其中，cΓ=｛ciΓ，i=1，2，……，nc｝ 是混合系数矩阵，由能量泛函对混合系数变分后得到本征值方程，求解本征方程得到的本征值为原子能级，本征矢为混合系数.

由于哈密顿量（5）仅包含了瞬时的纵向相互作用，为了得到高精度的理论计算结果，需要考虑横向相互作用（Breit相互作用）、QED效应和原子核效应对能级结构的影响［18-21］.本文采用微扰法考虑了以上各项对能级的修正，其中Breit修正项为：

QED修正项（自能项）为：

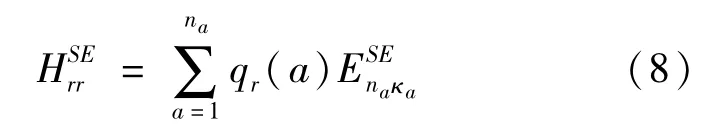
原子核效应修正项由普通质量修正和特殊质量修正两项，分别为：

为了检验波函数在近核区域的行为，研究等电荷态类锂电子序列波函数空间尺度的变化规律，本文还计算了近核处径向电荷密度，其表达式为［13］：

3 结果讨论与分析

本文利用全相对论理论框架下的GRASP2K程序包计算了类锂等电子序列1s22p 态的能级和径向电荷密度.在构造单电子轨道波函数的准完备基时，光谱轨道1s，2s，2p满足径向波函数节点条件，其余束缚轨道和连续轨道采用赝轨道进行描述，分别用n s，n p，n d，n f，n g，…….（n≥3）表示.电子关联作用1/rij进行多极展开时，不同幂次项对轨道角动量影响的需求不同，适当加入高角动量的轨道既可以充分考虑关联作用的影响，又可以加快计算收敛速度.

表1 给出了Ga28+离子1s22p 单轨道波函数准备基的构建结果.从表中可以看出，随着高角动量赝轨道的增加，准完备基组不断扩大，收敛较快，尤其是对于高离化的等电子序列，1/rij按照Z的标度变化.

在变分优化轨道波函数的过程中，MCDF方法充分考虑了电子关联效应，保证了基组的良好品质.利用优化好的波函数，进一步考虑Breit相互作用、量子电动力学效应和原子核运动效应对能级修正计后，得到类锂等电子序列（Z=31～40）22P1/2，3/2态的能级，如表2 所示.目前没有相关的实验数据和其他理论结果进行比较，希望能够有其他的数据对本文的结果进行检验.

为了进一步验证波函数的可靠性与准确性，利用表2 中数据可以完成类锂等电子序列（Z=31～40）22P态精细结构劈裂的计算.图1 给出了类锂等电子序列（Z=31～40）1s22p 态精细结构劈裂的算结果，图中分别描绘了本文结果和1/Z展开法、FCPC（Full Core Plus Correlation）方法的计算结果［22］.从图中可以看出，三种计算方法得到的精细结构劈裂按照Z4标度规律变化，遵循等电子序列变化规律.对于核电荷比较小的类锂体系，三种方法得到精细结构劈裂非常接近，基本相同；随着核电荷数的增大，相对论效应显著增强，仅考虑部分相对论修正的FCPC方法的计算结果逐渐偏离MCDF和1/Z展开法的计算结果，与二者之间存在偏差，而MCDF和1/Z展开法的计算结果基本一致.

表1 Ga28+离子单轨道波函数的构建（a.u.）Table 1 Atomic orbital wavefunction of Ga28+ion（in a.u.）

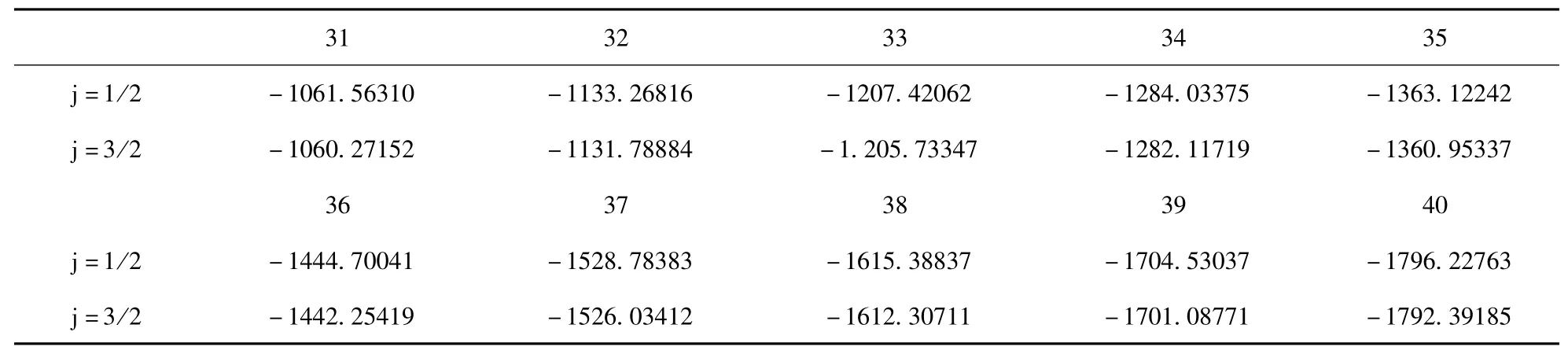
表2 类锂等电子序列（Z=31～40）22P1/2，3/2态的能量（a.u.）Table 2 Energies of 22P1/2，3/2state for Li-like isoelectronic sequence（Z=31～40）（in a.u.）

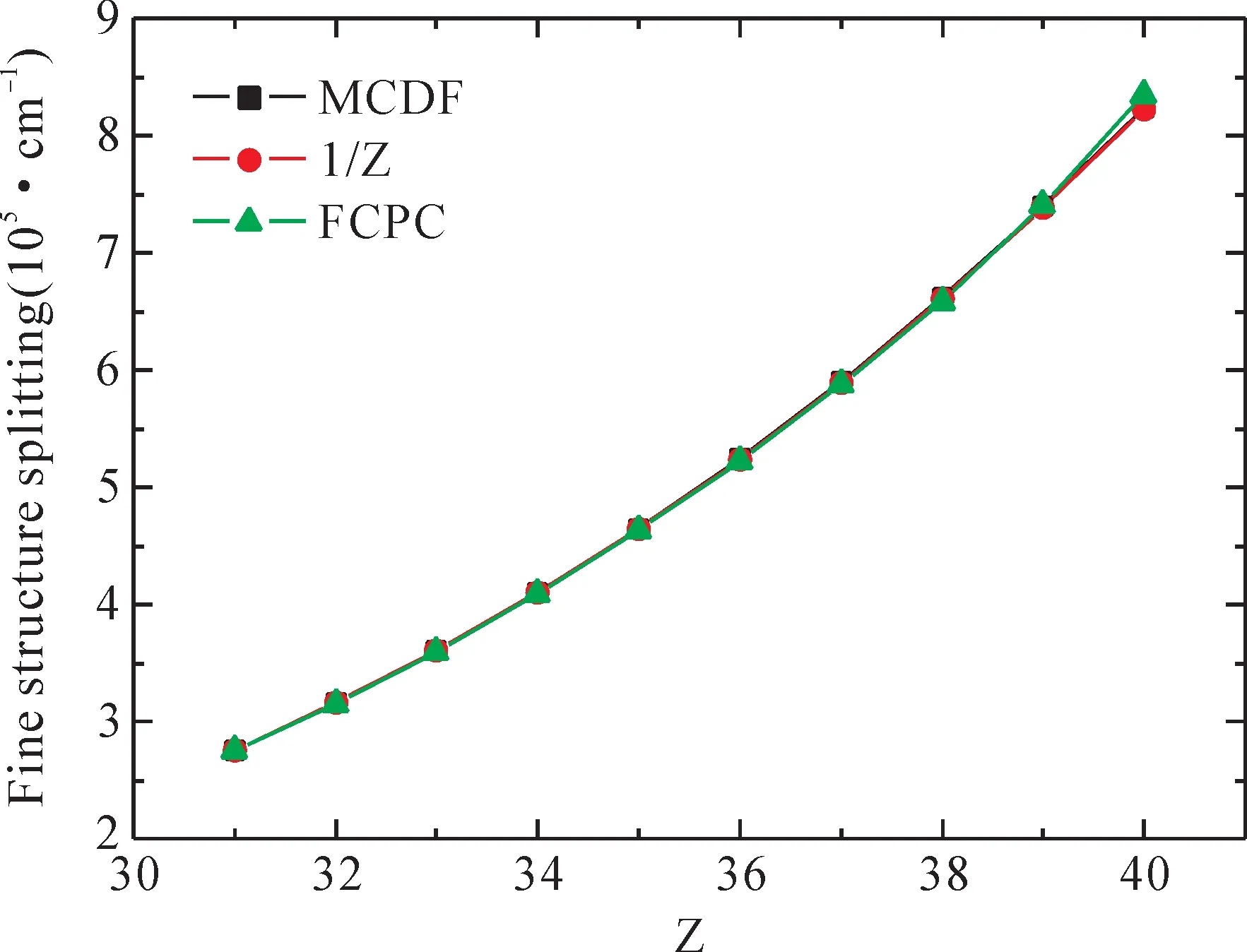
图1 类锂等电子序列（Z=31～40）1s2 2p 态的精细结构劈裂Fig.1 The results of fine structure splitting of 1s2 2p state for Li-like isoelectronic sequence（Z=31～40）

图2 是MCDF方法计算得到的类锂等电子序列（Z=31～40）1s22s和1s22p3/2态近核处径向电荷密度ρ（0）.可以清楚地看到，随着等电子序列核电荷数的增大，ρ（0）呈增大趋势，波函数向小r处收缩，体系空间尺寸减小，Z越大，离子的空间尺寸越小，电子被压缩到原子核附近越明显.对于高离化原子体系而言，随着空间尺寸的不断紧凑，电子间关联效应不断加剧.因此，理论上要求波函数对电子关联效应的描述要细致准确.利用本文波函数计算的径向电荷密度符合等电子序列的变化规律，进一步验证了波函数的可靠性，为后续研究提供了理论参考.

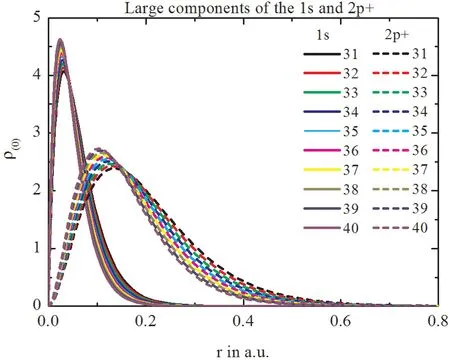
图2 类锂等电子序列（Z=31～40）1s2 2s和1s22p3/2态径向电荷密度Fig.2 The radial electronic density of 1s2 2s and 1s22p3/2states for Li-like isoelectronic sequence（Z=31～40）

4 结论

本文利用MCDF方法构建了类锂等电子序列（Z=31～40）1s22p 态的全相对论Dirac波函数，然后通过变分计算了1s22p 能级结构和径向电荷密度.MCDF方法直接包括了重要的相对论效应、电子关联效应和弛豫效应，得到的计算结果和其他理论方法的结果非常接近，符合等电子序列变化规律.研究结果表明，MCDF方法包括了足够多的相关组态，构造的波函数准确可靠，适用于离化度较高的多电子原子体系.随着核电荷数Z的增大，相对论效应对等电子序列能级影响逐渐增强，全相对论的MCDF方法的理论研究有助于揭示相对论效应对高电荷态类锂离子能级结构和性质影响的基本规律.另外，利用本文构造的波函数可以完成振子强度、线强、跃迁几率以及超精细结构的计算，进一步研究相对论效应对辐射跃迁性质的影响，同时，还可以检验波函数在整个位形空间的品质，丰富高电荷态离子的基本数据.