基于幅度相位联合校正算法的8-QAM自由空间相干光通信

李 林，吴志勇

(1.中国科学院长春光学精密机械与物理研究所，吉林长春 130033;2.中国科学院大学，北京 100049)

1 引 言

近年来，随着科学的高速发展以及技术日益成熟，激光被广泛地应用在了许多领域[1-5]。在这些应用领域中，自由空间激光通信以其无需频带许可、抗电磁干扰能力强、高安全性等诸多优点，逐渐引起了学者们的广泛关注[6-10]。

传统的自由空间激光通信系统主要采用二进制开关键控(OOK)的调制方式。这是由于基于OOK调制的系统结构简单、易于搭建。然而，这种系统的光谱效率较低，不适于超高速通信。

为了获取更高的光谱效率，研究人员尝试将QAM应用到自由空间激光通信系统中。QAM系统能充分地利用光信号的幅度和相位来传递信息。但是，由于受到大气湍流的影响，接收端信号的幅值和相位都会产生很大畸变，这会使得系统的误码率性能急剧恶化。文献[11]提出了一种速率可达720 Mbps的可见光QAM自由空间光通信系统结构，并在大气信道下对其进行了仿真验证。但是由于该系统并没有对大气信道所带来的干扰进行补偿，因此其存在着通信距离较短、误码率较高的问题。文献[12]提出了一种采用多模盲均衡算法的QAM自由空间激光通信系统。该系统能有效地抑制大气湍流引起的幅度抖动所带来的干扰，但是该系统却没有考虑并补偿大气湍流所引起的相位抖动、系统自身存在的固有频差以及激光器线宽所带来的影响。

为了解决以上问题，本文提出了一种基于幅度相位联合校正算法的8-QAM自由空间相干光通信方案。该方案无需信道信息辅助，仅利用接收端接收到的信号就可以实现对原信号的高精度还原。与此同时，该方案亦具有较高的光谱效率。实验结果表明该方案可以有效地克服大气湍流所带来的不良影响，并且拥有较好的误码率性能。

2 方案结构

本方案结构如图1所示。在系统的发射端，首先每3 bit二进制信息序列被电域8-QAM调制器转换成星座图如图中所示的同向(I路)和正交(Q路)两个支路信号。该星座图由两个调制指数不同、初始相位差为的QPSK星座图组成。随后，I路和Q路信号被加载到一个马赫-曾德尔调制器(MZM)上用以调制激光光束。被调制的光束经掺铒光纤放大器(EDFA)放大后，通过光学天线被送入大气信道。在这一过程中，发射信号可以被表示为:

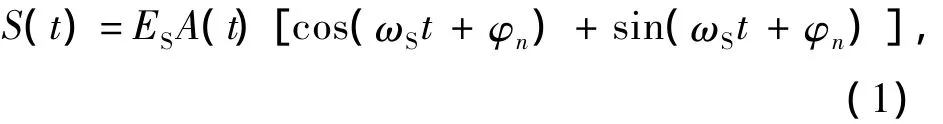
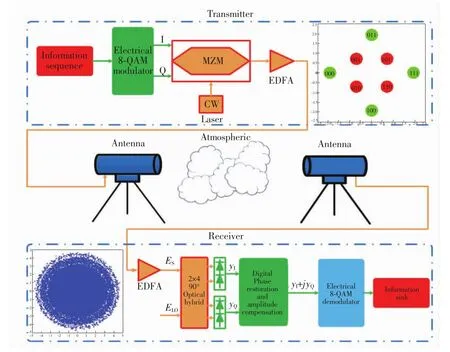
图1 方案结构模型Fig.1 Structure of the scheme model

其中ωS为载波的角频率，ES是载波幅值为被调制到载波上的相位信息代表被调制到I路和Q路上的幅度信息。式中an∈{C1，C2}为第n个符号同向分量和正交分量的幅值大小，C1、C2分别为星座图中内外两圈星座点的调制指数。g(t)为方形脉冲函数，TS表示符号间隔。

在接收端，首先接收到的信号被送入EDFA中进行放大。随后，相干接收机将对经过放大后的光信号ES进行探测。在这一过程中经过放大的信号光ES和本振光ELO的偏振态由偏振控制器来保证。相干接收机首先将信号光ES与本振光ELO送入2×4 90°光混频器中进行混频。随后，光混频器输出的光信号被平衡探测器(BD)转化为电信号供后续模块处理。平衡探测器(BD)转化所输出的电信号经采样后可以表示为:

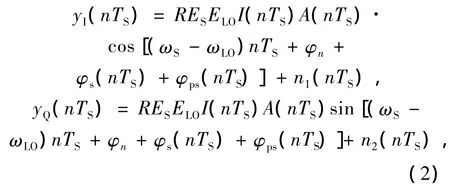
其中R代表探测器响应度，ELO代表本振光幅值。为了叙述方便，这里我们假设 R=1、ELO=1。I(t)代表由大气湍流所引起的光信号幅值抖动的随机过程，φs(nTS)代表大气引入的相位噪声。ωLO为本振光的角频率，(ωS-ωLO)nTS代表了本振光和载波之间固有频偏对信号相位的影响。φps(t)代表由激光器所存在的固有线宽引起的相位噪声，同时，我们假设每个符号间隔内由激光器联合线宽所引起的相位噪声差φps(t+TS)-φps(t)服从均值为0、方差为的高斯分布，其中Δf表示发射与本振激光器的联合线宽[13]。n1(t)和n2(t)则代表接收机中两条支路由于热噪声和散粒噪声所产生的高斯白噪声，这里设其功率均为。

3 幅值相位联合校正算法

经过平衡探测器后，信号被送入幅值相位联合校正模块。如图2所示，该模块由两部分组成:幅值补偿单元与相位恢复单元。首先，平衡探测器输出的I路和Q路信号被送入幅值补偿单元。为了求得大气湍流对信号幅值所造成的影响，该单元首先对两路信号进行平方求和运算，这一过程可以表示为:

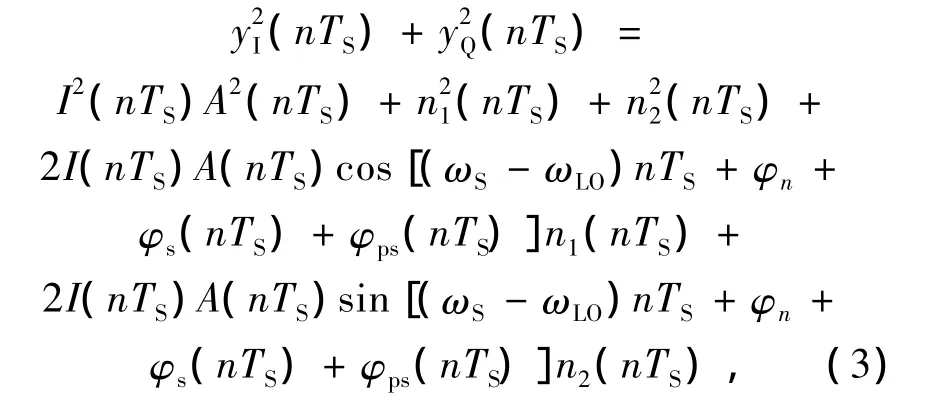
随后该单元对输出的N个结果进行平均运算，当N足够大时可得:

图2 联合校正模块Fig.2 Module of joint algorithm of amplitude compensation and digital phase recovery

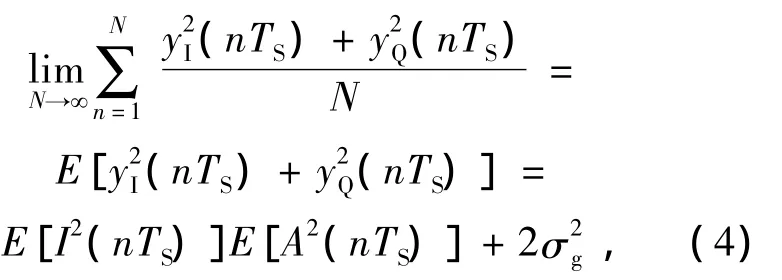
在实际的自由空间激光通信系统中，系统的发送速率(例如2 Gbps)远远高于大气湍流的频率(通常为kHz)。因此对于长度适中的一帧数据来讲，大气湍流所引起的信号幅度抖动可以被视为一个常数I。因此可得:

其中Ig为系统通过N个数据的运算结果所得到的对大气湍流所引起的信号幅值抖动I的估计。

随后，经过幅值补偿过的信号被送入相位恢复单元进行相位恢复。为了表述方便，我们首先假设系统的信噪比足够大，以至于可以忽略接收机中的热噪声和散粒噪声所带来的影响。

为了消除频偏所带来的影响，系统首先将上一级的输出信号R(nTS)与其延迟了一个周期的信号的共轭R*[(n-1)TS]相乘得到:

其中Δω=ωS-ωLO。随后，该单元对信号dn进行8次幂运算以移除调制相位信息。由于8(φnφn-1)=2πm(m为整数)，所以结果可以表示为:

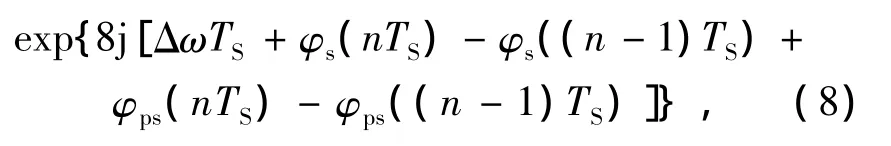
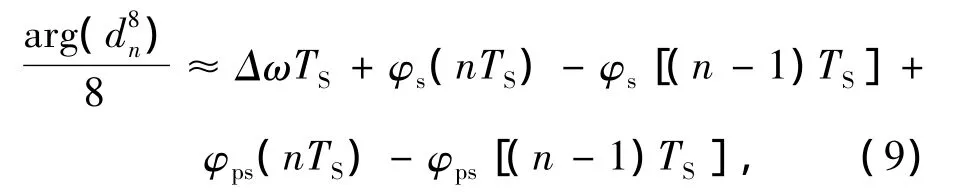
由上文可知公式(8)中φs(nTS)、φs[ ( n-1)TS]、φps(nTS)-φps[ ( n-1)TS]三项服从均值为0的高斯分布。所以，当M足够大时，对M个所得结果求平均可得:

随后系统会对信号进行频偏校正:

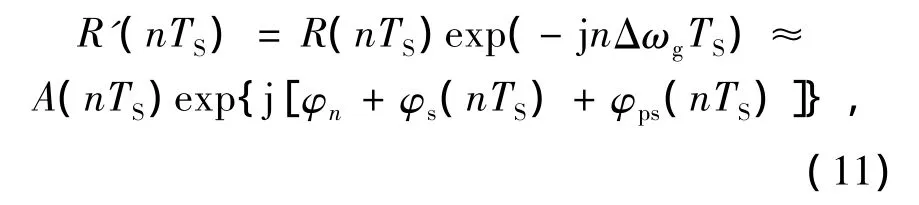
其中Δωg为系统通过M个数据运算结果得到的由频偏带来的角频率偏差Δω的估计。

在消除了频偏所带来的影响以后，相位恢复单元会对信号中所包含的相位噪声进行补偿。其具体过程如下:首先，系统对经过频偏校正的信号R'(nTS)进行取模运算，并通过数据比较器将结果与星座图中内外两圈间的调制指数门限进行比较，以确定当前信号的初始相位。随后，系统通过双路数据选择器以及乘法器将初始相位信息移除，以消除初始相位对后续相位噪声估计与补偿算法的影响。

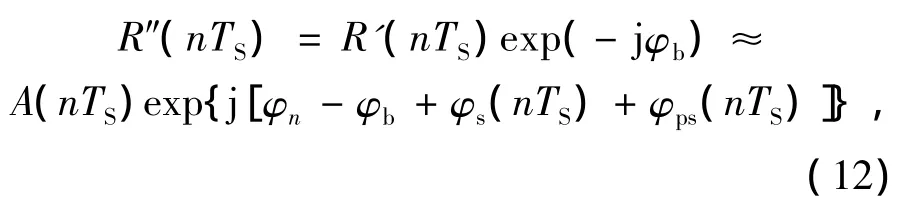
其中φb代表系统对信号初始相位的估计。然后，该单元对信号R″(nTS)进行四次幂运算以移除调制相位信息。由于4(φn-φb)=2πm(m为整数)，所以结果可以表示为:

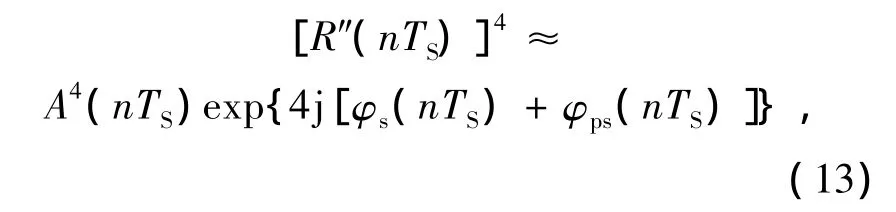
在得到[R″(nTS)]4后，该单元会对其角度进行求解，并将所得角度除以4，从而得到相位噪声信息:

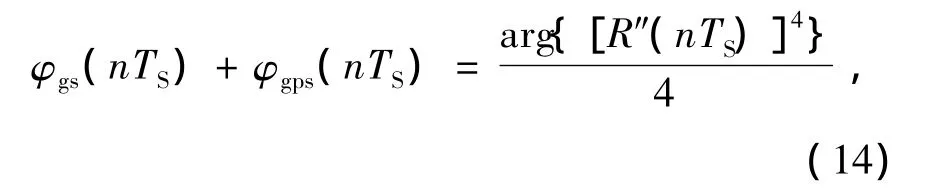
其中，φgs(nTS)、φgps(nTS)为系统对相位噪声φs(nTS)、φps(nTS)的估计。随后系统会对信号进行相位噪声补偿以获得最终的输出:

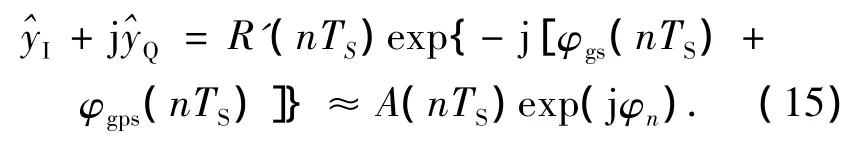
4 仿真实验

4.1 大气信道模型

大气湍流所引起的信号幅度抖动以及相位抖动是影响自由空间激光通信系统性能的最主要因素。在弱湍流条件下，信号的幅度抖动I服从对数正态分布:

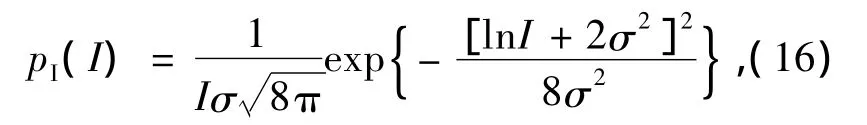
其中σ2为对数幅度方差，通常情况下，可以用Rytov方差表示为:

一般认为，大气湍流所引入的相位噪声φS服从均值为0的高斯分布，其方差可以表示为:

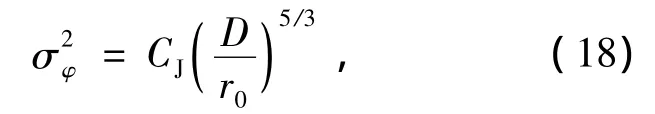
其中D为接收孔径，r0为大气相干长度，公式中的系数 CJ=1.029 9[14]。对于平面波以及 Kolmogorov湍流，大气相干长度r0可以表示为[15]:

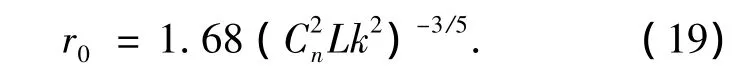
4.2 系统参数设计

我们利用MATLAB软件对文中所提出的方案进行了仿真实验。在实验中，我们对大气信道的模拟遵循上一小节所介绍的内容，信道的具体参数如表1所示。为了叙述方便，我们假设信号在大气中因长距离传输所产生的衰减是固定的，且可以被接收端的EDFA补偿。同时，我们假设系统的波长λ=1 550 nm、符号速率为2 Gbps、每帧数据的长度为106位、帧头导航序列长度为200位、幅值补偿算法的平均长度N=200、频偏校正算法的平均长度M=400、调制指数

表1 信道参数Tab.1 Parameters of the channels used in numerical simulation

4.3 仿真结果及分析

图3为当频偏f0=20 MHz、激光器联合线宽Δf=10 kHz时，系统在的大气湍流条件下的接收端信号各阶段的星座图。从图中可以看出，由于大气湍流、系统频偏、激光器线宽等因素影响，平衡探测器输出的信号和原信号相比产生了较大的畸变。而经过幅值补偿后信号的弥散现象得到了很好的抑制。随后的频偏校正极大地降低了系统故有频偏所带来的影响。而最后的相位补偿则将星座点进一步向理想位置压缩。

图3 联合校正系统接收端信号各阶段星座图。(a)平衡探测器输出的信号星座图;(b)经过幅值补偿后的信号星座图;(c)经过频率矫正后的信号星座图;(d)经过相位矫正后的信号星座图。Fig.3 Constellation diagrams of different stages at the receiver of the system using joint algorithm.(a)After BDs.(b)After amplitude compensation.(c)After frequency recovery.(d)After phase compensation.

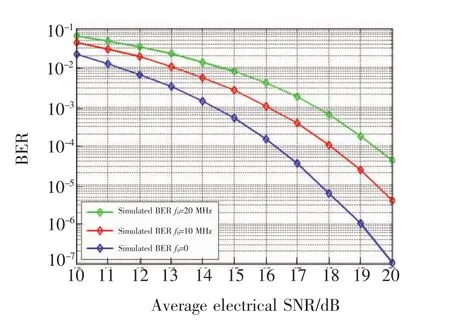
图4 具有不同频偏的联合校正系统仿真误码率Fig.4 Simulated BERs of the system using joint algorithm with different frequency offset

图5 具有不同联合线宽的联合校正系统仿真误码率Fig.5 Simulated BERs of the system using joint algorithm with different linewidth

图6 联合校正系统在不同的大气湍流条件下的仿真误码率Fig.6 Simulated BERs of the system using joint algorithm over different turbulence channels

图6为系统在不同的大气湍流条件下的仿真误码率曲线。为了能更好地说明问题，我们假设各系统的频偏f0=20 MHz、激光器联合线宽Δf=10 kHz。从图中可以看到，本文所提出的系统的误码率会随着大气湍流的增强而发生微弱的退化现象。由此可见，本文所提出的方案对大气湍流的影响具有较好的抵抗能力。

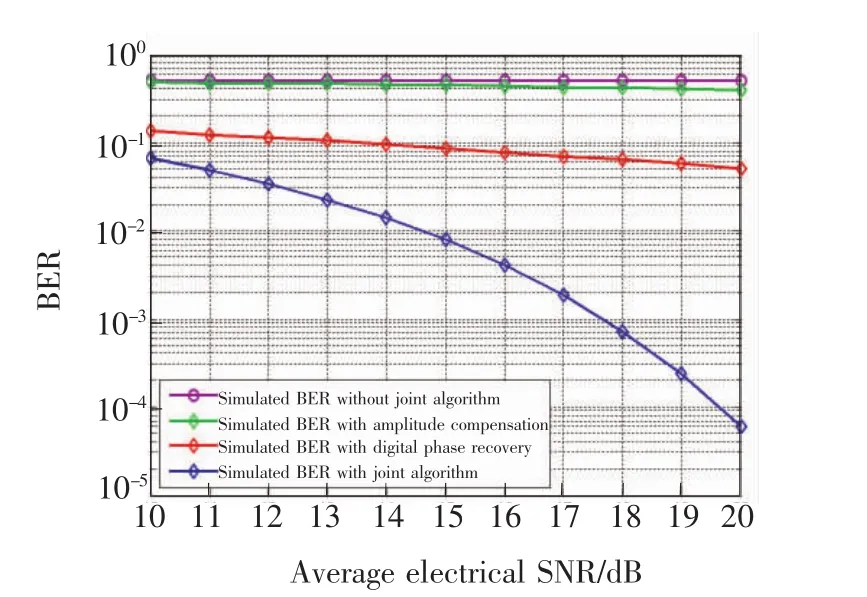
图7 不同系统的仿真误码率Fig.7 Simulated BERs of different systems

5 结 论

本文提出了基于幅度相位联合校正算法的8-QAM自由空间相干光通信方案。该方案无需信道状态信息就可以实现对信号的高精度还原，同时又具有较高的光谱效率以及可实现性。仿真实验表明，该方案能有效抑制大气湍流、激光器联合线宽以及频偏所带来的影响。与传统的8-QAM系统相比，该方案具有更好的误码率性能。因此，该方案有助于自由空间光通信的实现和性能提升。