基于期权合约的供应链协同决策研究

田 军，田 晨，董赞强

（1.郑州航空工业管理学院经济学院，河南 郑州 450046；2.河南大学商学院，河南 开封 475001；3.郑州航空工业管理学院外国语学院，河南 郑州 450046；4.郑州航空工业管理学院智能工程学院，河南 郑州 450046）

1 引言

供应链被描述为一个涉及供应商、产品制造商、批发商、零售商和消费者的系统，该系统包含了从供应商流向消费者的物流和信息流，同时，在供应链中也存在各种竞争关系。不同供应链成员最关心的是各自目标的最优化，这种自我服务的状态经常导致较低的供应链性能，然而，如果供应链上各企业通过签订转移支付合约实现协同运作，企业参照供应链目标制定各自目标，则供应链可以达到最优性能。

传统供应链管理往往只注重供应链成本的降低或供应链流程速度的提高，而忽视供应链的全方位价值增值。供应链企业所关注焦点是最终客户所获取的价值，供应链管理是以最终客户价值最大化为管理目标，而最终客户价值最大化则以有效满足最终客户需求为实现手段，这就要求在合适的时间和地点，以恰当的方式和价格，将合适的产品提供给合适的用户，在这种协同决策管理模式下使供应链达到利润最大化。这种模式中，供应链上各个节点企业在制定工作计划（如生产计划、库存计划、配送计划、销售计划等）时由供应链上各企业共同参与，如以期权合约方式实现风险规避，通过零售企业与生产企业共同分析预测市场需求及引入期权合约，改进了计划和补货的过程和质量，最终达到提高供应链效率、减少库存和提高消费者满意程度的目的，最终提高零售商和供应商的利润。尤其在网络环境下，要全面提升供应链的价值和核心企业业绩，就要充分促进供应链各节点企业之间及各个环节之间的协调、交流与沟通，建立科学有效的管理运行机制与管理体系，不断优化节点企业，形成利润最大化的价值同盟，确保供应链链条的完整性和协调性，从而提升整个供应链企业的影响力和竞争力。

当前，在供应链管理（SCM，supply chain management）研究方面，协同供应链（Coordinating Supply Chains）研究是一个备受关注的热点研究问题之一。在协同供应链研究中，Pasternack提出的买方回 退 合 约 （buy-back contracts）、Cachon 和Lariviere［1］提 出 收 益 共 享 合 约 （revenue sharing contracts）、Taylor［2］提出的销售折扣合约（sales rebate contracts）、Moorthy［3］提 出 的 数 量 折 扣 合 约（quantity discount contracts）和数量柔性合约（quantity flexibility contracts）等供应合约模型均表现出较高的效能。Li Jian［4］等对三级逆向供应链（主要包括回收商、再制造商和共享信息的分销商）中各关键成员之间的协作策略问题进行了探讨，并对部分协作策略模型进行最优化分析。

Trkman和Mccormack 等［5］提出利用供应链商的一些关键因素（供应链商特点、绩效和环境）确定供应链风险状态，并探讨了一些相应的风险控制方法。李书娟等［6］分析双渠道二级供应链模型中供应链的风险分布状态，对比分析了由供应链的供应方操控的竞争模式与由供应链供应方和购买方合作的协作模式，得到了零售商与制造商进行协作的契约条件。Wu等［7］和Halukas等［8］讨论了供应链风险的重要性问题。Zhu等［9］假设供应链上下游中供应方和购买方的风险呈现风险中性状态，对比分析了供应链中解决渠道冲突的传统模式和通过逆收入共享策略协调的合作模式。Chernonog 和Avinadav［10］对双渠道供应链及其风险规避方式进行研究，同时对双渠道供应链最优产品定价问题进行了分析研究。Neiger等［11-12］提出依据价值过程确定供应链风险的一些措施。Yoo［13］对双渠道的二级供应链中的风险分布情况进行解析，并给出供应链供应方与购买方实现期权合约的解析条件。王虹和周品［14］研究了双渠道供应链风险规避的最优策略，探讨了期望与方差对双渠道供应链市场需求的影响。

金融衍生品市场的产生与发展是现代金融领域发展取得的最大成就之一，而能有效控制风险的期权合约是金融衍生工具之一。通过期权合约，供应链中的企业能够避免产品价格风险，供应链中涉及期权合约的相关研究工作取得了较多研究成果，如Barnes-Schuster等［15］对基于期权的供应链柔性问题进行了深入研究；Xiaolong Wang等对在市场信息实时更新情形下，如何应用期权合约协调零售商主导的供应链问题，且基于Stackelberg 游戏理论，其建立一个仅包括一个供应商和一个零售商的供应链模式，在此模式下，零售商通过设计合约协调供应链的生产状态；Hantao Li等针对期权和远期合约，探讨了供应链的估价问题；于春云等［16］在需求具有价格敏感性条件下，构建了收益共享契约模型，提出了零售商分享制造商网络渠道部分利润的逆收人共享策略；Spinler等［17］探讨了在二元供应链（dyadic supply chain）中提高经济效率的期权方法。上述研究表明，期权合约问题在供应链研究领域中备受关注。

尽管许多论文研究了基于期权合约的供应链风险问题，但是针对随机需求状态下的期权合约供应链问题进行探讨的论文相对较少。对此，论文分析了在市场需求和价格不稳定情况下，供应链上下游之间如何通过构建期权合约协同机制实现风险规避问题，研究供应链购买方需求不确定时，供应商如何通过在二级供应链中引入实物期权将订货量及价格等关键不确定风险转移向供应方，同时来自期权合约的额外收益又在一定程度上平衡了供应方的风险损失，如此构建了基于期权合约的供应链协同管理利润最大化模型，通过期权因素利润决策机制平衡供应链中购买方与供应方的收益变动，实现市场需求随机变动下的供应链整体利润最大化，同时，分析了供应链中购买方与供应方的决策性能，在供应链上下游之间构建基于期权合约的最优战略模型。

2 问题模型描述及一些引理

针对双渠道供应链系统（单一零售商构成的零售渠道和一个制造商主导的网络渠道），为在最大程度上实现供应链系统风险规避的目的，本文主要探讨基于期权合约的供应链协同决策模型，以供应链上下游各方利润为参变量的切入点，展开具有期权合约与协同决策机制的供应链决策模型的分析，围绕供应链整体利润最大化为目标进行决策，以此得到双渠道供应链系统在协同决策下利润的数学目标展示。一方面针对传统双渠道供应链系统环境，构建未考虑期权合约的利润模型，并对供应链整体利润参未考虑期权合约的利润模型E（πbs）=E（πs）+E（πb）（其中πbs表示整个供应链的利润，πs表示供应方利润，πb表示购买方利润。），并对供应链整体利润参量进行较为深入的分析；另一方面针对双渠道供应链系统，构建具有期权合约和供应链系统关键成员协同运作的供应链利润模型

E（）=E｛R［Q-（θ（D）+q-Q）+］+c0q+hs［（θ（D）+q-Q）+］+X［（D-Q）+］-ksθ（D）-w［（Q-θ（D）-q）+］｝（模型中参数具体含义见下面关键术语阐述），并详细分析利润最大化的关键因素。通过上述两方面的利润模型理论分析，描述了基于期权合约的协同供应链决策模型的显著优势，实现供应链系统总体利润最大化。论文所提模型中提出的假设条件及关键参量描述如下：

（a）考虑包含一个供应方和一个购买方的多周期供应链，供应方可能是一个产品制造商或者商品批发商，购买方可能是供应链下游的一个商品批发商或一个商品零售商；

（b）供应商和零售商共享完整的信息（供应方与购买方之间的信息是对称的）；

（c）购买方具有随机需求状况，供应方有随机的产额分布；

（d）购买方可以通过期权合约管理需求的不确定性；

（e）供应方和购买方均是风险中性的（risk neutral）。

关键术语阐释：

P表示购买方单位销售价；R表示供应方单位销售价；hb表示购买方的残值；hs表示供应方的残值；D表示购买方从供应方取得的订货量；θ（D）表示供应方的随机产量；q表示购买方具有期权合约的商品期权订货量；c0表示期权合约单位销售价；X i（i=1，2）表示第i个期权合约执行中商品期权执行价格；Q=Q（X1，X2）表示购买方在某一时间t的随机需求层次；k b表示购买方每一订单的订购成本；ks表示供应方的生产成本；k表示购买方在物品短缺时产生的购买成本；w表示供应方在违反合约时的违约成本；c=c（D）=c（D，θ（D））表示因供应方引起的在购买方产生的其它成本；f（·）表示时间t时刻供应链期权合约商品的价格，它用来描述市场随机需求的密度函数；F（·）表示t时刻描述市场随机需求的分布函数；πb表示购买方利润；πs表示供应方利润；πbs表示整个供应链的利润。

现在利用供应链期权合约商品定价模型来描述一下期权执行价格与利率之间以及依赖它们的供应链期权合约商品价格间的关系。不妨设供应链商品市场满足：

（1）供应链商品市场为弱有效市场；

（2）无交易费用和税收；

（3）允用将全部所得卖空供应链期权合约商品；

（4）在供应链商品期权有效期内无红利支付；

（5）商品期权交易是连续的。

设商品价格遵循如下几何Brownian运动

其中，X表示购买方期权合约执行中商品期权执行价格，t为即时时间，μ为供应链期权预期收益率，σ为供应链期权执行价格的瞬时波动率，dz1为Wiener过程，且。

假定利率r也遵循某种关于时间t的随机过程，它满足如下ITO 过程：

其中，a（r，t）是利率r的漂移率，且

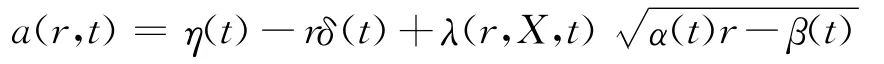
b（r，t） 是 利 率 的 波 动 率，且b（r，t） =是市场的风险 价格，dz2是Wiener过程，且ε2～N（0，1）。

若刻划期权执行价格X与利率r之间的相关因子为ρ（-1≤ρ≤1），则根据参考文献［18］中引理2 和参考文献［19］中引理4 的分析结果可知：，

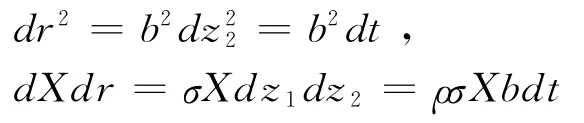
引理1：假若供应链期权合约商品的价格f由期权执行价格X、利率r及时间t决定，则由参考文献［18］中定理结论知：

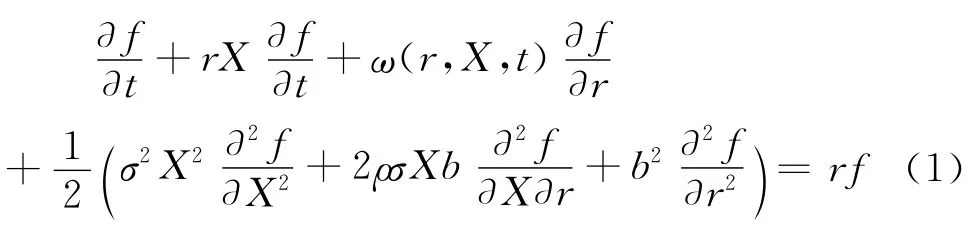
其 中ω（r，X，t）=a（r，t）-b（r，t）λ（r，X，t）=η（t）-rδ（t）表示一类额外的市场风险，它仅取决于标的变量r、q和时间t，而与证券的性质无关。

特别地，如果a（r，t）=b（r，t）=0，从方程（1）便可得到金融领域著名的Black-Scholes偏微分方程：

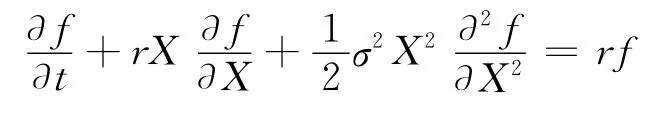
这也说明，Black-Scholes期权定价方程是基于混合过程供应链期权合约商品定价模型的一个特例。另外，若令则方程（1）就演变成为一个有关零息商品期权定价模型：

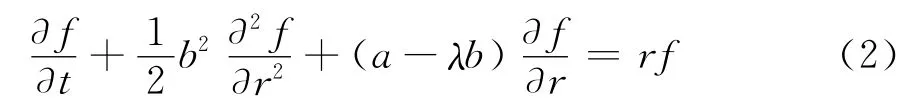
值得注意的是，方程（2）能够较好地验证金融学科Ho和Lee（1986）所建立的有关面值为q0的零息供应链期权定价模型：

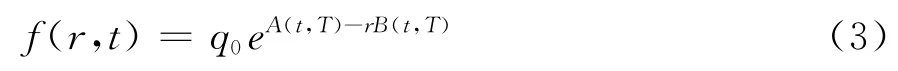
将式（3）代入方程（2），有：

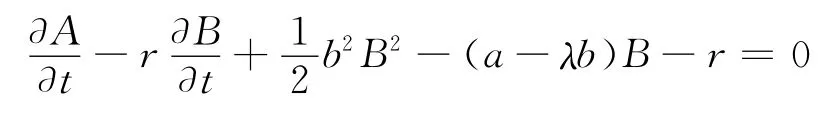
对上式进行两次关于r的微分，可得到：

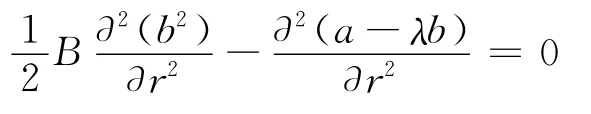
因 为B是 关 于T的 函 数，而a（r，t）、b（r，t）、λ（r，t）与T无关，因此：

从a（r，t）、b（r，t）的表达式不难看出，方程（4）恒成立。

由方程（4）可知，式（1）描述的供应链期权合约商品定价模型对应的解，是求解n+1元二阶偏微分方程问题，对这样一个二阶偏微分方程求解是相当困难的。为此，我们仅讨论任意两种期权定价的模型，我们不妨来讨论两种期权的定价问题。

引理2：设期权交易中在任意两种不同期权运作模式下，商品期权执行价格X1和X2在风险中性世界中遵循如下几何Brownian运动：

其中，ai（X1，X2，t）、bi（X1，X2，t）（i=1，2）分别是X i的预期收益率和价格波动率，是Wiener过程，εi～N（0，1），（i=1，2）。

本文定义，依赖于X1和X2的供应链购买方商品价格为f=f（X1，X2，t），由上述d X1、d X2表达式和f（X1，X2，t）泰勒展开式知：

则有：

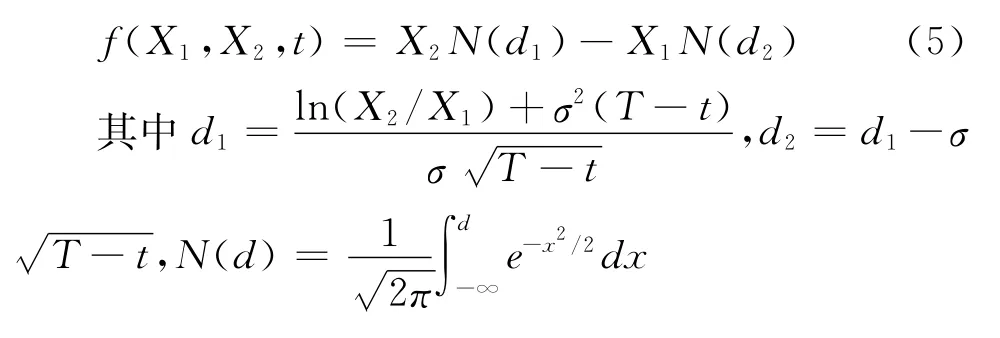
N（d）表示正态分布。

证明：考虑供应链购买商品价格X1和X2与f的组合：1时，不难算得：

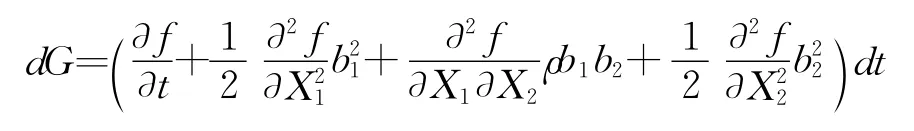
其中ρ是dz1与dz2间的相关系数。

因此，当无风险利率为r时，根据无套利原则，有：

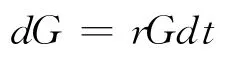
即

若b1=σ1X1，b2=σ2X2（σ1、σ2为常数），则上述方程变成为：

为求满足方程（6）的供应链期权合约商品的价格f（X1，X2，t），不妨设定f（X1，X2，t）的终期收益价格为：f（X1，X2，t）=max（X2-X1，0）

则方程（6）的约束条件为：

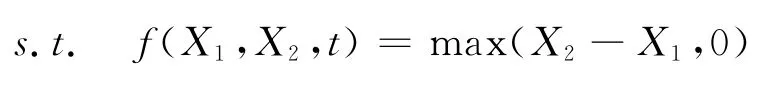
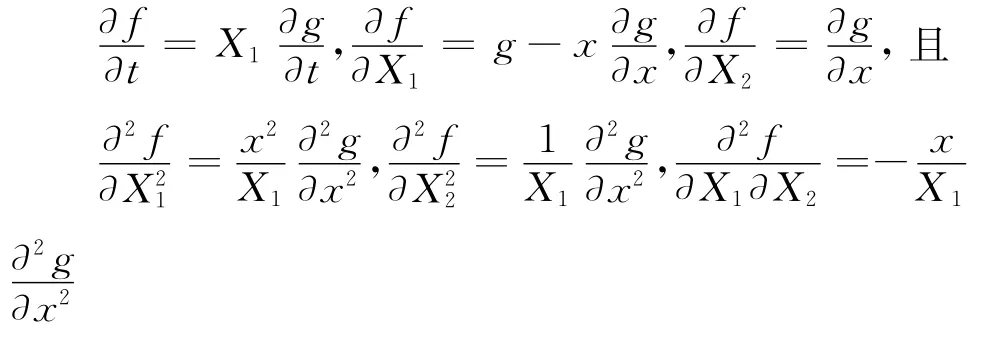
从而方程（6）可化简为：

且约束条件变为：

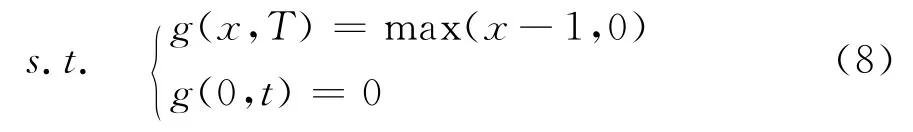
满足约束条件（8）的方程（7）可视为无风险利率为0、执行价格为1的标准看涨期权的价格所对应的微分方程。此时期权合约的价格波动率σ=σ21+σ2-2ρσ1σ2。因此，根据Black-Scholes期权定价公式得：g（x，t；T）=c（x，t；T）

所以，方程（6）的最优解为：

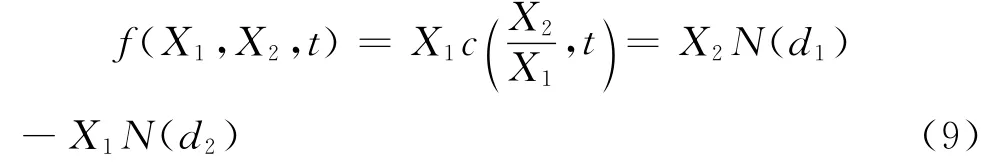
这就是执行价格X1和X2的供应链购买方商品价格为f=f（X1，X2，t）的解。

证毕

根据供应链决策模型利润最大化，可以分析供应链中考虑期权合约的购买方与供应方决策关系（供应链利润模型，式（14）和（19）描述），在那里f（·）表示t时刻供应链期权合约商品的价格，描述市场随机需求分布函数F（·）的密度函数，f（X1，X2，t）=f（Q（X1，X2）），Q（X1，X2）表示购买方在某一时间t的随机需求层次，它随着X i的变化而取不同的值。

3 基于利润最大化的供应链决策模型分析

3.1 供应链中未考虑期权情况下的购买方与供应方决策性能分析

基于上述假设，设 （y）+=max｛y，0｝，购买方的利润描述为下述函数：

若c为D的线性函数，且0。在未考虑期权情况下，供应方利润函数描述为：

且当c为常量时，供应链的整体利润相对容易获取。

3.2 供应链中考虑期权情况下的购买方与供应方决策性能分析

期权合约描述了在支付一定量的期权费后，在未来某一时期，购买者有权以执行价购买或卖出一定数量的资产。如果超过了约定的期限，期权自动终止，且如果期权持有者未执行相应权利，持有者的最大损失仅是期权费用损失，因此，期权持有者可达到规避风险的目标。

对供应链上游企业，期权也是有利的，它可能同下游企业签订卖出合约，如此上游企业有权以执行价卖出潜在资产，这避免来自上游企业的价格下跌风险。

不失一般性，在某一供应链环境中，为满足购买方和供应方利润，设存在关系ks＜R＜c0+X＜P，w＞ks＞hs，w＞ks＞hb，X＞hs，X＞hb，其中X为期权执行价格，描述在期权合约执行价与期权合约单位售价之和介于购买方供应方商品单位售价，且供应链上商品期权执行价均大于商品生产和商品订购成本，同时，商品期权违约成本高于供应方商品生产成本及购买方商品订购成本，则依据前述假设和期望函数定义，购买方的期望利润描述为：

式（14）中f（Q）=f（Q（X1，X2））由式（9）给出，式（14）描述在扣除期权交易成本c0q（期权购买成本）情况下购买方期望利润模型，这里c0表示期权合约单位销售价。式中第1项来自销售项目的买方收益；第2项描述在供应方商品供应与购买方购买需求随机动态变化情况下，在购买方引入期权订货参变量q后产生的残值项的收益；第3项描述整个供应链上商品产量随机变化情况下所支付给供应方的费用；第4项描述供应链上随着期权订货量q的不同引起商品短缺产生的成本。

针对市场需求随机变化引起购买方商品订购量随机动态变化的情况，期权合约中商品期权订货量q与商品期权单位销售价c0满足πb（q）= （PX）Min（q，Q）-c0q，πb（q）表示市场需求Q随机变化中购买方收益变化量，Min（q，Q）表示期权合约执行中购买方执行期权订货量与市场需求量之间的较小量，（P-X）描述期权合约执行中购买方的单位 商 品 净 收 益。 同 时，由即可推得期权合约执行中购买方最优期权订货量q满足

从Pr｛Q≤T｝=F（T），Pr｛a＜Q≤b｝=F（b）-F（a）和Pr｛Q＞T｝=1-F（T）（a、b满足0≤a＜b，描述市场存在正向需求，且需求在有限区间［a，b）变化），可推得：

进而，Hesse矩阵行列式可描述为：

当P+d＞h b，Hesse矩阵为否定矩阵，E（πb）取最大值，特别当θ（D）=λD，λ≥0且为一常量，计算下面的算式（17）：

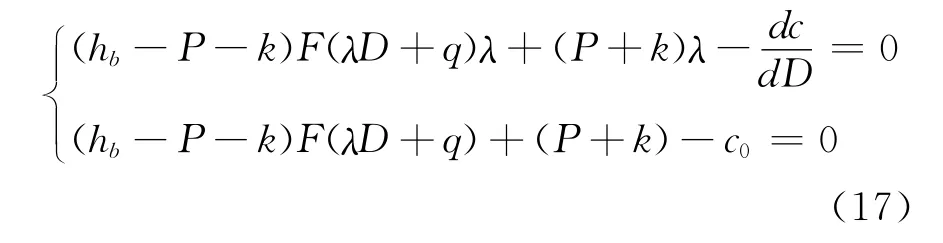
得到：

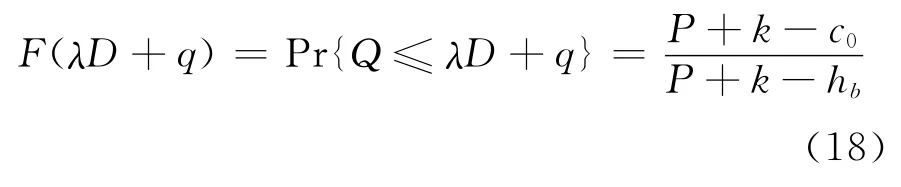
对于供应方，其期望利润可描述为：

式（19），期权参量q、v满足关系πs（c0）=（c0-c）q+XMin（q，Q）+v（q-Q），πs（c0）表示供应方的期权合约收益，其期望收益满足关系E［πs（c0）］=，基于上文中q=，代入上文E［πs（c0）］等式得到供应方期权合约销售量的期望收益模型：，其中v描述了供应商单位剩余产品的残值。同时，依据最优期权合约销售量与期权合约定价之间的对应关系，可推得q=

进一步计算得：

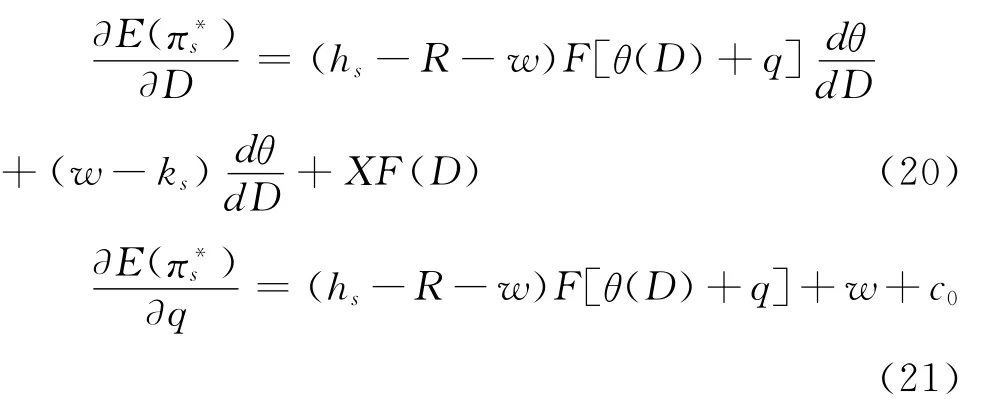
当θ（D）=λD，可推得：w）f（λD+q）λ2+Xf（D）

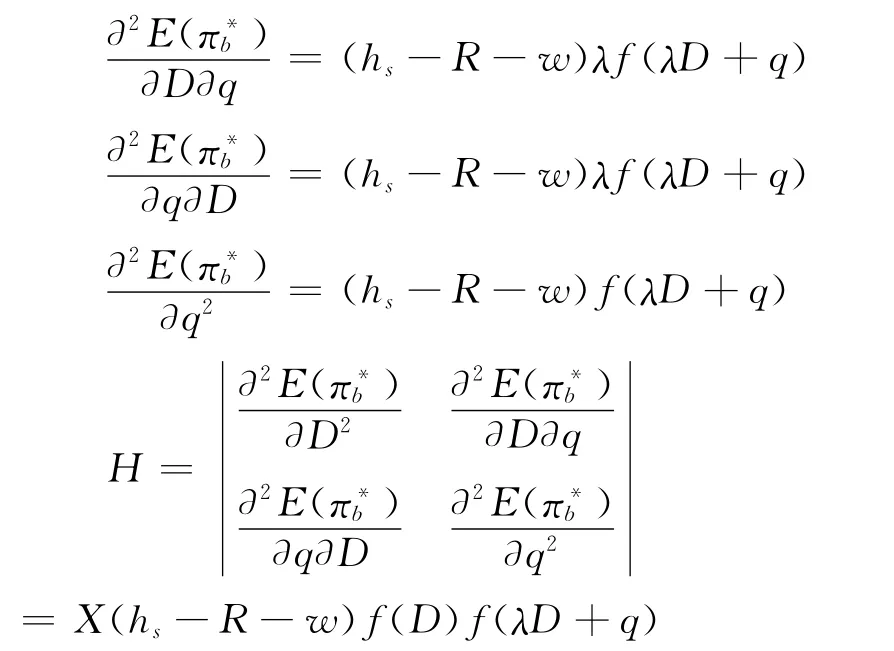
若hs≤R+w，Hesse矩阵是否定矩阵。依据下式（19）：

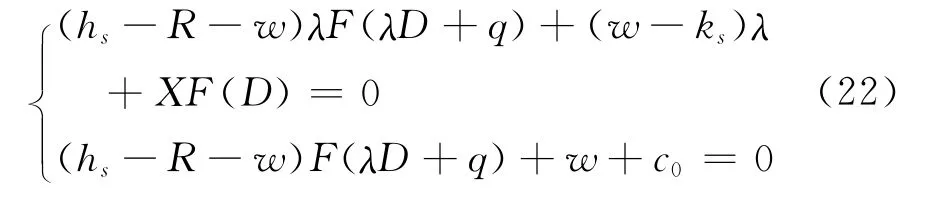
依据极值原理得：

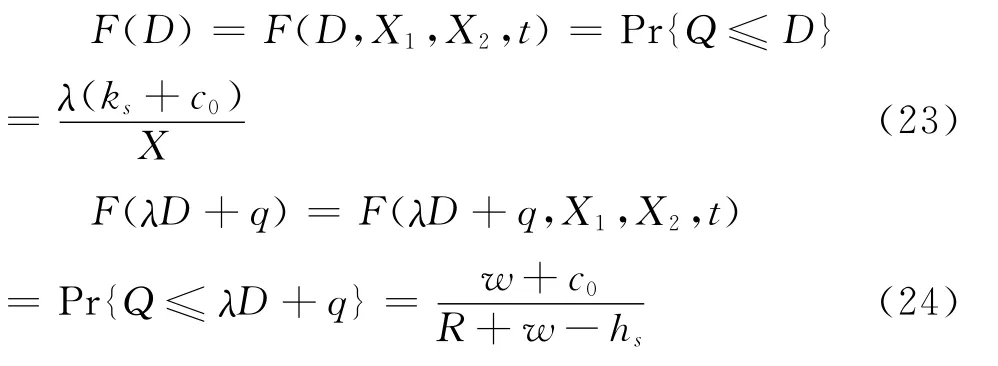
从式（19）推得，在考虑期权合约情况下，供应方的利润能被容易计算得到。

从（23）可以看到，在期权合约执行价与期权合约单位售价之和介于购买方供应方商品单位售价，且供应链上商品期权执行价格均大于商品生产和商品订购成本时，则商品期权违约成本高于供应方商品生产成本及购买方商品的订购成本。

4 数值实验与结果分析

4.1 数值示例

通过一组数值实验验证文中所提模型的可行性与有效性，观察期权合约因素对供应链利润（供应方和购买方利润）的影响。为了对论证和分析文中模型的有效性，本节将利用相应的数值示例进行深入分析。设产品零售价P=100，产品生产成本ks=30，期权合约执行中商品期权执行价格X=50，q保持购买方具有期权的价格，市场需求Q服从［0，100］的均匀分布。依据设定的参数和期权合约利润模型（式（2-5））可计算出商品供应方对期权的定价c0=25.36，商品批发价（远期合约的定价）R=73.62。根据建立的利润模型、期权订货量模型以及期权合约中风险转移策略，对供应链上期权订货量、购买方利润和供应方利润量分别进行数值分析比较。

4.2 灵敏度分析

在数值示例分析中，以期权合约中期权执行价格与期权订货量变化量描述供应链中风险水平，分析风险水平对供应链上期权合约订货量与远期合约（批发价合约）订货量的不同影响状态，同时，分析在供应链上执行期权合约和远期合约情况下，供应链上价格成本、期权执行价和残值收益的变化对商品供应方与购买方收益产生的不同结果。

图1 风险偏好水平r对决策与利润影响

图1（a）描述不同风险状态（因市场动态变化，购买方采取不同层次的商品实时紧急采购价e）下，供应链中风险水平r（以ΔX／Δq描述供应链风险水平）对最优期权价格的影响，图示当紧急采购价格相对较低时，最优的期权价格随着风险偏好系数r的增加而增加，原因在于当r变小时，购买方的风险程度增加，从而期权订购量降低，而在供应链运作中，为激励购买方多订购，供应方会降低期权价格来获得更多的利润；而当紧急采购价格中等或较髙时，最优的期权价格随着r的增加单调不增，原因在于存在缺货成本风险，当r变小时，为了避免因商品短缺而带来的损失，购买方可能会多增加订货量，从而商品供应方会相应地提髙期权价格。图1（b）描述了展示了在不同情形下购买方的风险状态对最优期权订货量的影响。从图1（b）中可以看出，购买方的期权订购量随着风险偏好系数r的增加单调不减，即当供应链风险水平逐渐增高时，应用期权合约机制，供应链购买方的风险在一定程度上被规避，购买方订购的期权订货量逐渐增大，但在风险变化中，较低区段的商品实时紧急采购价对应的期权商品订货量变化幅度相对高于较高区段商品紧急采购价对应的商品期权订货量，原因在于期权合约风险规避优势及供应链利润增加驱动。

图2 价格因素对供应链购买方与供应方利润影响

图2描述了价格成本系数ρ（以ΔX／（Δk+Δkb+Δw）描述）在［0，1］的范围内变化时，供应连中购买方与供应方比例系数变化趋势。图2（a）图示展示，随着供应链价格成本的增加，购买方对应的利润逐渐减少。图示展示期权合约下利润状态优于远期合约（基于批发价的合同合约）的利润情况，原因当价格增长时，购买方订货量减少，零售商会减少订购量，成本价格也就越大，零售商自然会减少订购量以节约成本，同时，市场销售量也相对降低，购买方利润降低，但在期权合约中，存在供应方向购买方进行转移支付，弥补了购买方损失，因此，期权合约下购买方利润情况优于基于批发价的远期合约。图2（b）描述了供应链上供应方利润随价格变化情况，图示展示随着价格增大，供应方利润不断增大，但在采用期权合约情况下，供应方利润增长更为明显，且当价格成本系数ρ≥0.3，两种合约对应的供应方利润偏差逐渐增大，其原因在于采用期权合约机制，供应方执行期权价格和期权订货量，这高于远期合约批发价格和订货量，期权合约下利润相对增加。

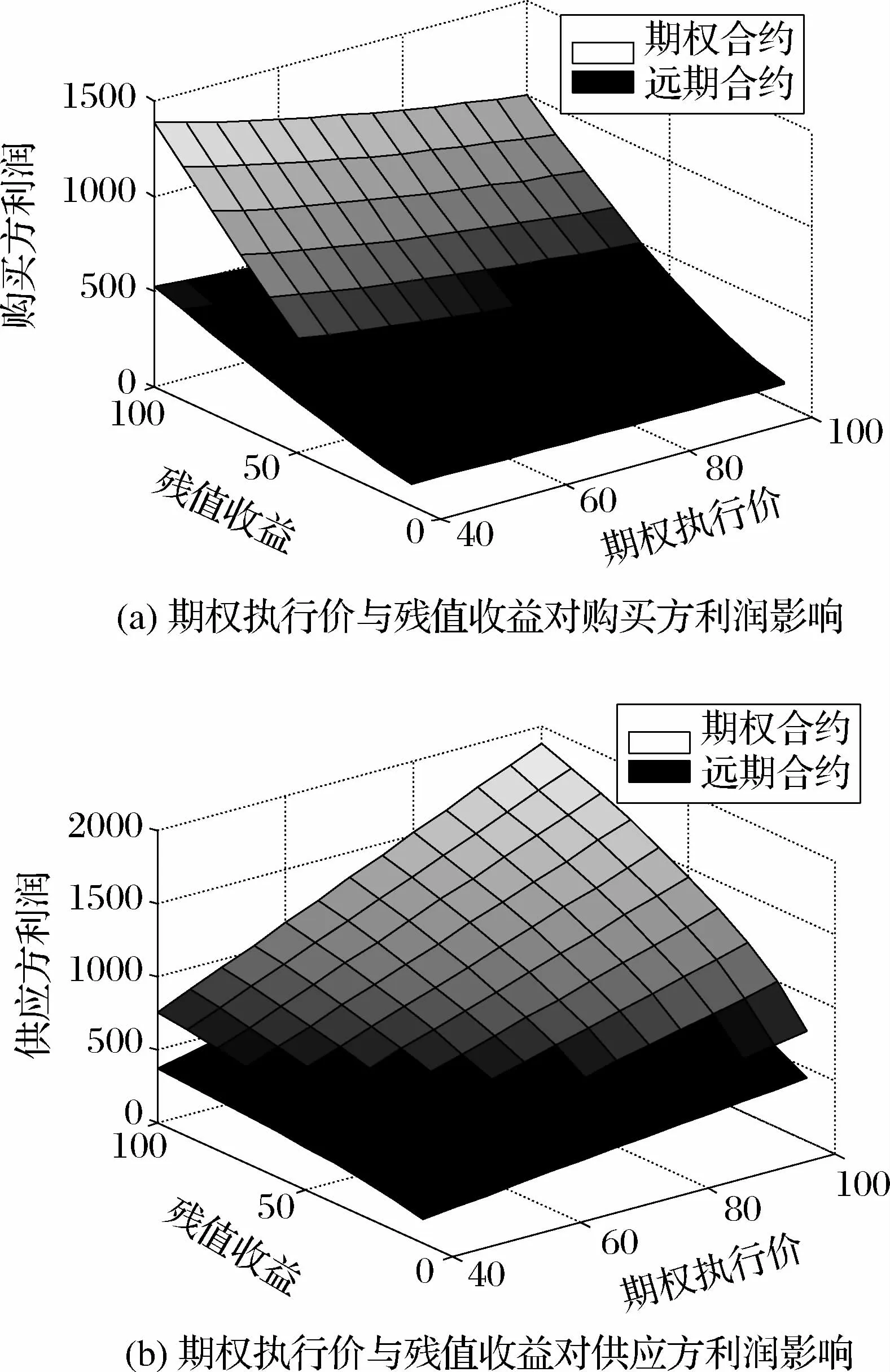
图3 期权执行价与残值收益对购买方与供应方利润影响

图3分析了商品残值收益与商品期权合约执行价对供应链上购买方和供应方收益的影响。设定残值hb与h s取值范围为［0，100］，商品期权执行价X取值范围为［40，100］，依据参数可计算出供应链中供应方对远期合约与期权合约的定价值，基此可得到购买方与供应方的利润状态。图3（a）描述随着商品残值hb收益增大，期权执行价降低时，购买方利润逐渐增大，在执行期权合约（上方图）情况下，利润增长的幅度高于远期合约（下方图）对应的利润，且当残值hb≥50，X≤80时，两种合约对应购买方利润偏差变化更为显著；同时，在商品残值收益相对较低，商品期权执行价增大情况下，执行商品远期合约（批发价合约）情况下，购买方将取得较好利润。图3（b）描述随着商品残值hs收益与商品期权执行价逐渐增大时，商品供应方利润逐渐增大，但在执行商品期权合约（上方图）情况下，利润增长的幅度相对远期合约（下方图）较为明显，且当hb≥50，X≥80时，两种合约对应的利润偏差变化更为显著。

5 结语

在供应链系统中，供应链上的产品制造商的角色不仅表现为商品的供应方，同时作为供应链下游的商品零售商竞争者角色体现，这在很大程度上增加了供应链上下游各方的风险状况，如供货风险和商品积压风险等较为突出风险，如此在供应链上采取不同的风险规避策略机制的不同，将在较大程度上影响供应链系统运作的有效性，甚至将影响整个供应链系统的存活期，这也是供应链系统研究领域备受关注的热点问题之一。对此，本文从双渠道供应链系统上各个核心关键成员协同运作的方面进行研究，引入基于期权合约的供应链风险回避决策控制模型，以实现整个供应链系统整体利润最大化。具体研究内容体现为，在供应链上下游之间引入期权合约模型，分析了购买方与供应方的决策优化问题，进一步地，构建具有期权合约的供应链风险决策模型，通过对已构建的供应链风险决策模型中关键参数的概率分析与推导计算，进而建立了具有期权合约的供应链购买方与供应方利润模型。最后，基于数值仿真实验分析，进一步验证了本文提出的基于期权合约的供应链协同决策模型的有效性。

本文的研究可得到如下结论和启示：针对解决商品市场需求随机变动、供货竞争激烈、产品积压和价格随机波动等供应链上突出风险问题，由本文的研究内容及笔者已有研究成果发现，在供应链上核心成员之间实时以协同方式运作，如信息的协同共享、市场需求随机波动下的协同定价和风险协同规避等，如此在一定程度上确保供应链上各关键成员利润的最大化，也使得供应链整体利润最大化，利润最大化是各成员形成供应链的关键基础，对供应链的稳定性及生存期具有重要影响。对此，本文中的研究基于期权合约的供应链协同决策利润模型是解决供应链风险问题的有效方法，通过在供应链成员间引入期权变量，实现对供应链风险的协同控制，使供应链各方利润在均衡中达到最大化，以此实现供应链整体利润的最大化。论文提出的模型对双渠道两级供应链体系进行详细研究，后续研究将探讨具有期权合约的多渠道网络化多级供应链协同风险管理体系问题，进一步完善和解决供应链风险规避协同策略问题。