二维驱动机构的机电一体化谐振问题探讨

黎 枭， 魏新生， 杨 杰， 高雪松， 周华俊

（1.上海航天控制技术研究所，上海201109；2.上海惯性工程技术研究中心，上海201109）

0 引言

在空间姿态执行机构中，控制力矩陀螺、地基（空基）望远镜和二维指向跟踪系统是卫星等空间飞行器实现快速姿态机动和高精度的重要单机部件。这些重要单机部件经设计、加工和装配完整后，各个部件的谐振频率固定，而由两个或多个零部件连接在一起所组成的机构谐振频率也随之确定。因多部件耦合而产生的谐振在机电一体化设备中非常普遍[1]，主要包括电机与传感器、负载内部、电机框架在机械框架内的耦合，但大多数谐振由电机与负载之间的动力传动而引起[2-3]，还有一种由零速时摩擦力矩奇异而产生。文献[4]、文献[5]证明了当静摩擦大于库仑摩擦时，采用PID控制必然出现极限环振荡；采用库仑摩擦模型进行补偿的优点在于模型简单、易于实现，但由于该摩擦模型是静态模型，且其无法描述零速时摩擦力表现出的 “Stribeck”效应，其控制效果受到了限制。为此，很多学者提出了相应的改进措施。文献[6]采用了一种基于库仑摩擦模型的自适应补偿控制，该文献的仿真和实验结论也证明了采用 “Stribeck”摩擦模型能够更准确地描述摩擦现象，从而消除谐振，实现提高补偿精度的效果。此外，消除系统谐振的方法通常包括如下几类:

1）减少控制回路的带宽:此方法在工程中非常普遍，在设计各类驱动控制器时留有一些余量，可以降低动态响应，对过程不作要求，只是强调指令发出多少时间后成像；

2）增强机械连结刚度[3]；

3）利用电机速度反馈增加滤波器，以减少谐振[7-8]；

4）增加电机与负载之间的阻尼[9-10]；

5）通过观测预估的方法减少谐振，以提高性能[11-12]。

本文采用了双反馈控制来抑制谐振，以二维驱动机构作为研究对象，其结构示意图如图1所示，并对其驱动控制系统进行了建模仿真及实验。以电机自带增量式角度反馈引入电流环和速度环控制器，及负载（方位轴或俯仰轴）上绝对式角度反馈引入位置环控制器（双反馈控制），同时配合notch滤波器，即能够克服因电机间接驱动所引起的谐振问题，得到较好的动态性能指标，该方法在工程中得到了很好的应用[13]。

图1 二维驱动机构示意图Fig.1 Diagram of two-dimensional drive mechanism

1 电机力矩驱动控制模型

图2为二维驱动机构电机力矩传动示意图（涡轮涡杆用齿轮代替），图3为涡轮涡杆力矩传递特性，其电机力矩传动流程图如图4所示，图中各字母符号的定义如表1所示。在图4中，IC经过电流控制器得到IF，它与电机力矩系数KT相乘得到TE，电磁力矩直接驱动电机惯量JM引起加速度AM，对它积分得到ωM，再次积分得到θM。 由图2可知，电机通过传动轴与涡轮涡杆连接，而涡轮涡杆两对齿轮（原边与副边）又是相互咬合的，其通过摩擦力矩来传递，再通过传动轴作用到负载（方位轴或俯仰轴）。所以，电磁力矩按照图4的电机力矩传动流程图分别可以产生AL、ωL和θL。

图2 电机传动示意图Fig.2 Schematic diagram of motor drive

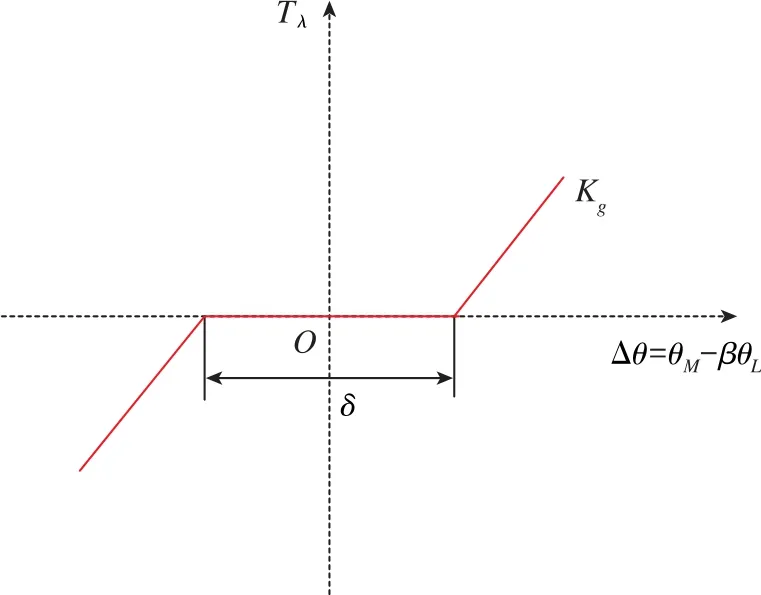
图3 涡轮涡杆传动特性Fig.3 Transmission characteristics of turbine vortex rod

图4 电机力矩传动流程图Fig.4 Flow chart of motor torque transmission

当θM与ωM之差落在齿轮间隙δ/2之内时，负载因没有力矩作用而保持静止状态。只有当两者之差超过δ/2时，负载因外力矩作用而产生运动。根据图4，可以推导出θM与TE、ωM与TE的传递函数关系式

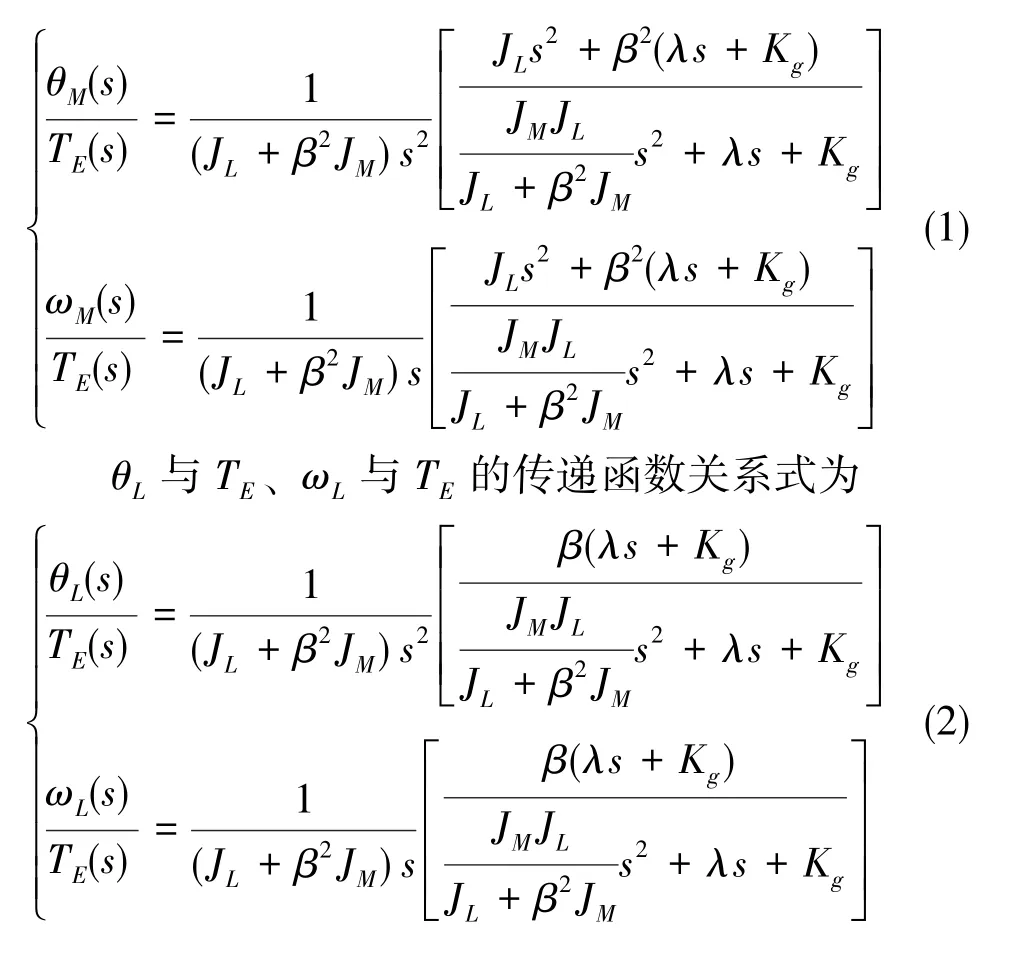
因无法获得传动机械的耦合刚度Kg和交叉耦合粘性阻尼λ的准确数值，只能根据以往经验先给定一个参考值进行仿真，其参数参考值如表2所示，然后通过实验对物理参数进行修正。ωM/TE的幅频特性和相频特性、ωL/TE的幅频特性和相频特性分别如图5和图6所示。

表2 电磁力矩传动参数Table 2 Transmission parameters of electromagnetic torque

由图5、图6可知，当频率约为80Hz时，电机端和负载端均出现了谐振，而图5在约65Hz时出现了反谐振。对比式（1）和式（2）可知:负载端的传递函数θL/TE、ωL/TE的分子项少了s2项。在低频时相频特性不明显，但随着频率的增加，当频率达到60Hz时，电机端和负载端均与电磁力矩信号存在90°的相位差，从图5和图6的相频特性也可以得到佐证。根据式（2），由于传递函数θL/TE、ωL/TE的分子项少了s2项，在低频区域控制时性能不会有明显变化，但在高频区域控制时性能下降就会凸显。因此，为了伺服控制系统能获得好的动态响应性能，需要添加电机反馈信号，形成双反馈控制电路模型。

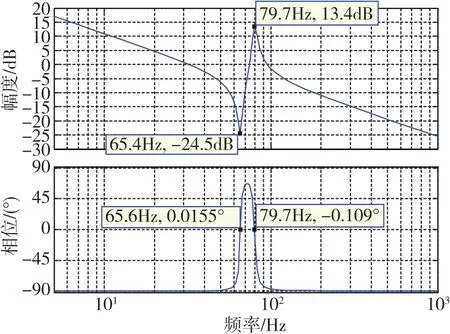
图5 电机角速度与电磁力矩比值ωM/TE的幅频特性和相频特性Fig.5 Amplitude-frequency and phase-frequency characteristics of the ratio of angular velocity to electromagnetic torque （ωM/TE）

图6 负载转速与电磁力矩比值ωL/TE的幅频特性和相频特性Fig.6 Amplitude-frequency and phase-frequency characteristics of the ratio of angular velocity to electromagnetic torque （ωL/TE）

2 Notch滤波器设计

使用 “Chebyshev type 1”IIR数字滤波器，数字采样频率为1kHz，通带内衰减为1dB，阻带内衰减为40dB，中心频率为80Hz。根据设计目标设计一个8阶滤波器，设定fpass1＝60Hz、fstop1＝75Hz、fstop2＝85Hz、fpass2＝100Hz， 其传递函数表达式如式（3）所示，式（3）中所设定的参数如表3所示。

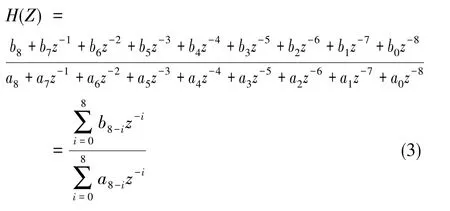
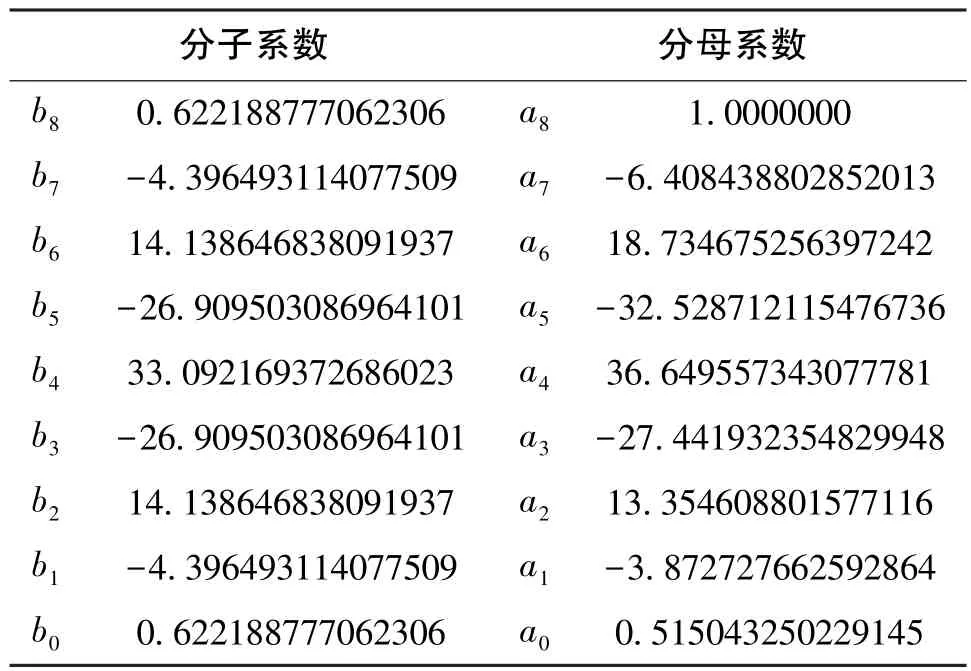
表3 IIR数字滤波器系数Table 3 Parameters of IIR digital filter

利用Matlab进行仿真，分别得到幅频特性、相频特性和零极点分布，如图7～图9所示。由图9可知，4对共轭复极点都落在单位圆内，1对3重共轭零点都落在单位圆上，即式（3）符合设计的要求。因此，此滤波器是稳定的。根据传递函数画出如图10所示的时域流程图，然后按时域流程图加入到电流控制器中。

图7 notch滤波器的幅频特性Fig.7 Amplitude-frequency characteristics of notch filter

图8 notch滤波器的相频特性Fig.8 Phase-frequency characteristics of notch filter

图9 notch滤波器零极点分布图Fig.9 Pole zero distribution of notch filter

图10 离散域信号流程图Fig.10 Flow chart of discrete domain signal

3 实验与结果

二维驱动机构如图1所示，其方位轴和俯仰轴的伺服控制调试仍然是分开进行的，先调试方位轴。调试顺序为先电流环，再速度环，最后位置环，电流环以电机电流和电机自带增量式角度编码器（2500线/转）作为反馈，速度环以电机自带增量式角度编码器作为反馈。性能符合要求后，再将负载端（方位轴）绝对式编码器引入闭环控制系统，如图11所示。当控制性能达到要求后，再调试俯仰轴。当两轴都调试好后，即可进行同步控制。两轴的转动惯量、传动比及伺服电机参数如表4所示。

表4 二维驱动机构传动系数Table 4 Transmission coefficients of two-dimensional drive mechanism

图11 方位轴（俯仰轴）双环控制信号流程图Fig.11 Flow chart of azimuth axis（pitch axis）double-loop control signal

以绝对式码盘的读数为准，取23位高有效位（绝对角度29位）， 设定的速度指令为ω＝10（°）/s。图12为未加notch滤波器电路的速度阶跃响应时域波形，图13为方位轴以ω＝10（°）/s转动时电机A相电流的波形。由图12的时域波形可知:在未加notch滤波器时存在1个明显的干扰信号，对此波形进行频率分析得到1个频率约为80Hz的干扰波形，此信号严重影响控制性能，使伺服跟踪控制结果无法满足要求。另外，对图13中电机A相电流频谱进行分析，也得出1个频率约为80Hz的干扰信号。图14为加上notch滤波器电路时速度阶跃响应时域波形，将其与图12进行对比可知:加上notch滤波器后，频率约为80Hz的干扰信号明显被减弱，方位轴的速度转速精度大大提高。

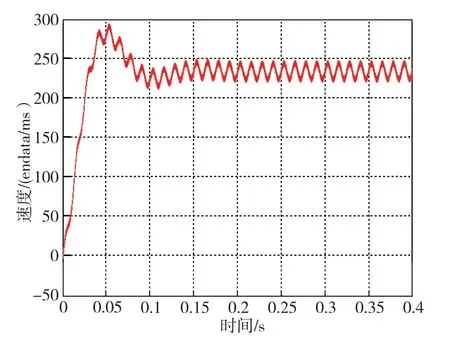
图12 未加notch滤波器时的速度阶跃响应时域波形Fig.12 Time domain waveform of velocity step responds without notch filter

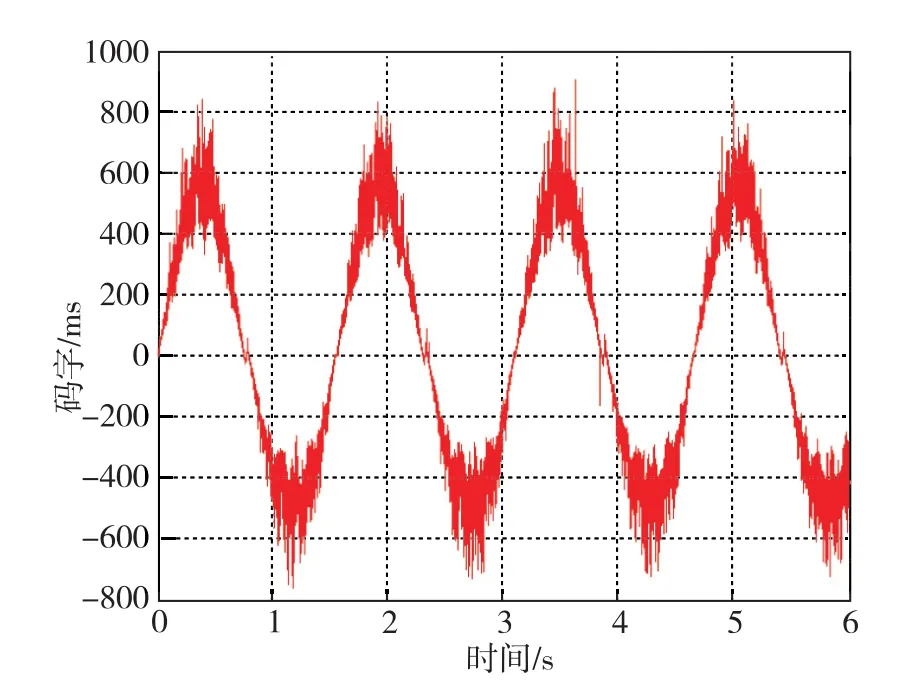
图13 方位轴匀速（ω=10（°）/s）运行时A相电流波形Fig.13 A-phase current waveform when azimuth axis runs at a constant speed

图14 加上notch滤波器后的速度阶跃响应时域波形Fig.14 Time domain waveform of velocity step responds with notch filter

4 结论

本文结合二维驱动机构两轴的控制系统特点分别对传动系统各个环节的耦合进行了建模和仿真，并从时域和频域两个方面分析了系统的抗扰能力和控制带宽。当加上notch滤波器电路后，驱动机构的速度转速精度明显提高，从而增强了系统的抗干扰能力，验证了方案的可行性。当将二维驱动机构调试好后进行再搬离，需重新装配使基座与地面的连接刚度满足要求，这给系统带来了很大的困难。但通过增加数字滤波的方式可满足系统对抗干扰能力的高性能要求，此方式不仅成本低，也具有很好的推广价值。