机抖激光陀螺捷联系统动力学建模及结构动特性设计方法

赵 欣，魏 伟，张 杰

（1.北京航天时代激光导航技术有限责任公司，北京100094；2.空装驻北京地区第四军事代表室，北京100041；3.北京控制与电子技术研究所，北京100038）

0 引言

激光捷联惯性导航系统以其性能稳定、工作寿命长、精度高、环境适应性好等优点被广泛应用于运载航空、航天、武器、舰船、汽车等领域[1]。目前，激光捷联惯性导航设备主要采用二频机抖激光陀螺作为其敏感器件，二频机抖激光陀螺采用抖频偏频技术消除了闭锁效应的影响，从而提高了陀螺的测量精度[2]。陀螺的抖动效率和本体响应与其结构参数密切相关:一方面，结构参数设计不合理可能影响陀螺的抖动幅度，使得陀螺测量精度下降，甚至失去功能[3]；另一方面，陀螺抖动成为激光惯导不可避免的激励源带动本体产生伪圆锥运动[4-5]，对陀螺的测量造成误差，结构参数设计不合理可能导致本体响应过大，进而降低陀螺的测量精度。

目前，研究结构参数对惯性单元抖动效率及测量误差的影响主要有两种方法:1）直接进行多体动力学仿真或有限元仿真[3-6]；2）进行动力学理论建模和分析[7-9]。采用有限元仿真的方法相对直观，但是难以提取规律性的结论；采用动力学理论建模的方法进行研究，更容易找到转动惯量、频率、阻尼等结构参数对抖动效率及测量误差的影响规律。吴美平等[7]较为完整地建立了激光捷联惯性导航系统的矢量动力学模型，从理论上分析了部分结构参数对圆锥误差的影响规律。李志华等[8]建立了激光惯组结构系统二自由度动力学模型，能够对系统抖动效率进行计算。但是，一方面，二自由度系统忽略了箱体刚度和转动惯量的影响，无法对其影响进行估计；另一方面，该研究也没有对各关键结构参数的影响规律进行具体讨论。

本文建立了激光惯导系统三自由度标量动力学模型，并结合Matlab仿真，从工程实际出发，得到了各结构参数对陀螺抖动效率和本体响应的影响规律曲线，总结了基于惯导动特性设计的激光惯导结构设计原则和方法，有利于实现激光惯导结构设计的定量化和标准化。

1 动力学建模

如图1所示，软捷联激光惯导的惯性测量本体（含陀螺、加速度计等惯性敏感器件）通过减振器与箱体实现连接。在惯性测量本体中，陀螺通过抖轮与本体结构实现连接。如图2所示，对物理系统进行简化，考察单陀螺的情况，将结构体的弹性和转动惯量进行分离，将物理系统简化为三自由度扭簧-质量-阻尼系统进行研究。由结构动力学基本理论[10]可建立激光惯导箱体—本体—陀螺三自由度动力学方程，如式（1）所示。

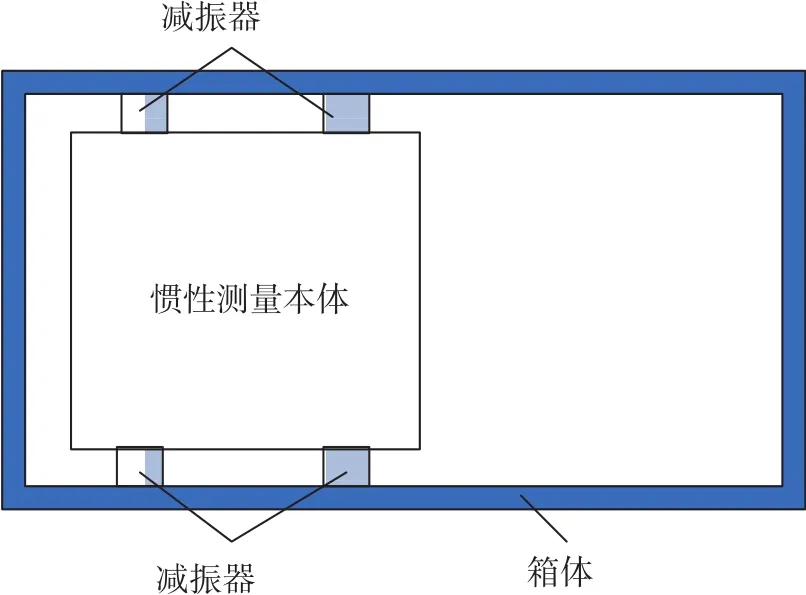
图1 激光惯导物理模型Fig.1 Physical model of laser inertial navigation system

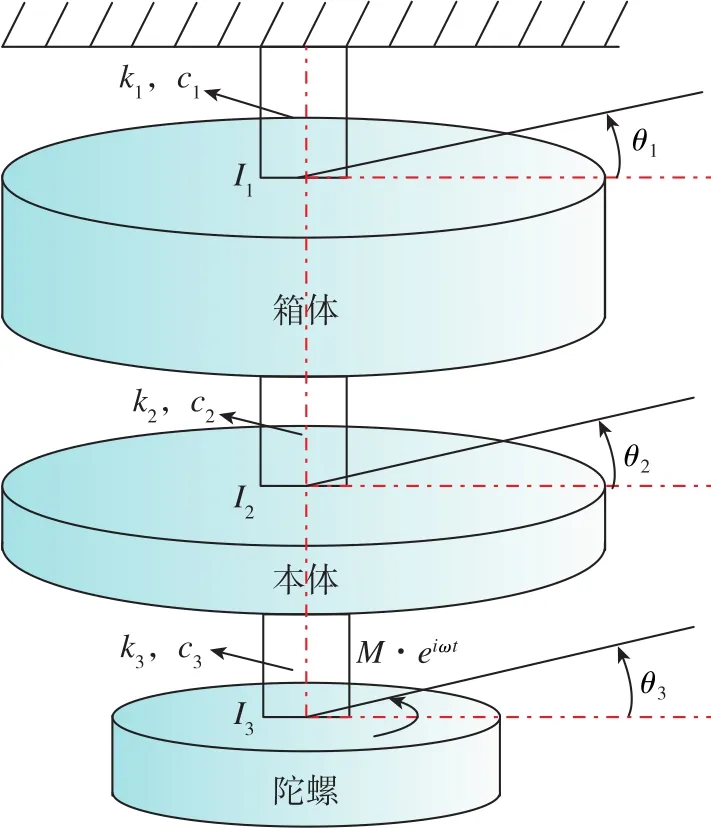
图2 激光惯导三自由度系统的简化模型Fig.2 Simplified model of 3-DOF laser inertial navigation system

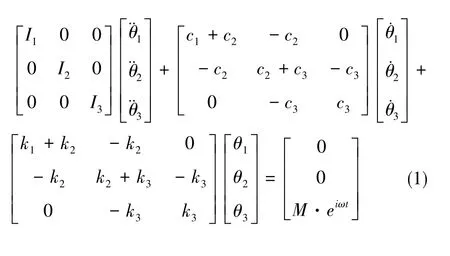
式（1）中，I1为箱体转动惯量；I2为本体转动惯量；I3为陀螺转动惯量；k1为箱体刚度；k2为减振器刚度；k3为陀螺抖轮刚度；c1为箱体阻尼系数；c2为减振器阻尼系数；c3为陀螺抖轮阻尼系数，包含结构阻尼、安装阻尼、材料阻尼等；θ1为箱体相对载体系转角；θ2为本体相对载体系转角；θ3为陀螺相对载体系转角；M·eiωt为陀螺抖动驱动力矩，所选取的转轴方向为陀螺抖动轴方向。

2 方程组求解

将式（2）～式（6）代入式（1）中， 经推导可得转角θ3的动力放大系数D3

3 参数获取与模型仿真验证

在推导出D1、D2、D3的表达式后，只需要确定系统参数即可精确求解。其中，I1、I2、I3（转动惯量）可通过CAD模型从工具软件中直接获取；p1、p2、p3（频率）和c1、c2、c3（阻尼）可通过产品试验获得；k1、k2、k3（刚度）可通过相应的转动惯量和频率求取。得到系统参数后，可通过Matlab求取系统幅频响应曲线，如图3～图5所示。

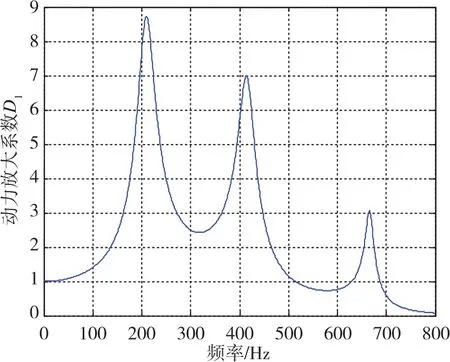
图3 陀螺抖动激励下箱体响应动力放大系数随激励频率变化曲线Fig.3 Response curve of the shell dynamic amplification factor with excitation frequency under gyroscope dither excitation

图4 陀螺抖动激励下本体响应动力放大系数随激励频率变化曲线Fig.4 Response curve of the IMU dynamic amplification factor with excitation frequency under gyroscope dither excitation

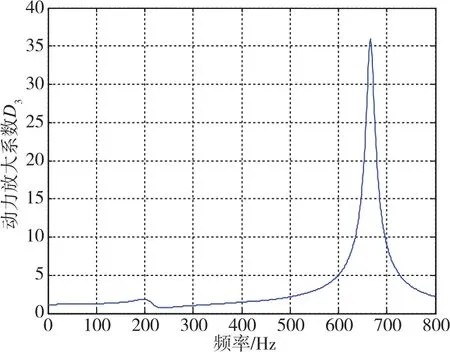
图5 陀螺抖动激励下抖轮响应动力放大系数随激励频率变化曲线Fig.5 Response curve of the dither mechanism dynamic amplification factor with excitation frequency under gyroscope dither excitation

经实际测试，安装于固定支座的单陀螺抖动放大系数一般为20～40，在计算中采用的抖轮安装阻尼比为0.0125。

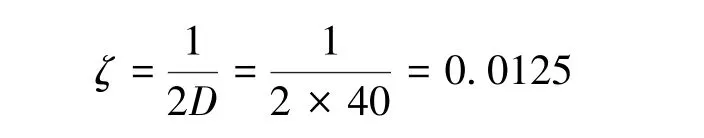
当将三自由度系统设置为质量无穷大或刚度无穷大时，都可以将一个三自由度系统等效为二自由度系统。将二自由度系统设置为质量无穷大或刚度无穷大时，都可以将其简化为一个单自由度系统。在三自由度模型中，将I1设置为一个较大值进行计算，结果如图6所示，这个结果与二自由度系统的计算结果完全一致。将I1和I2同时设置为一个较大值进行计算，结果如图7所示，这个结果与单自由度系统的计算结果完全一致。由此，三自由度系统的模型正确性可以得到验证。

图6 三自由度系统I1设置为一个较大值时得到的陀螺响应曲线Fig.6 Response curve of gyroscope when I1has a large value

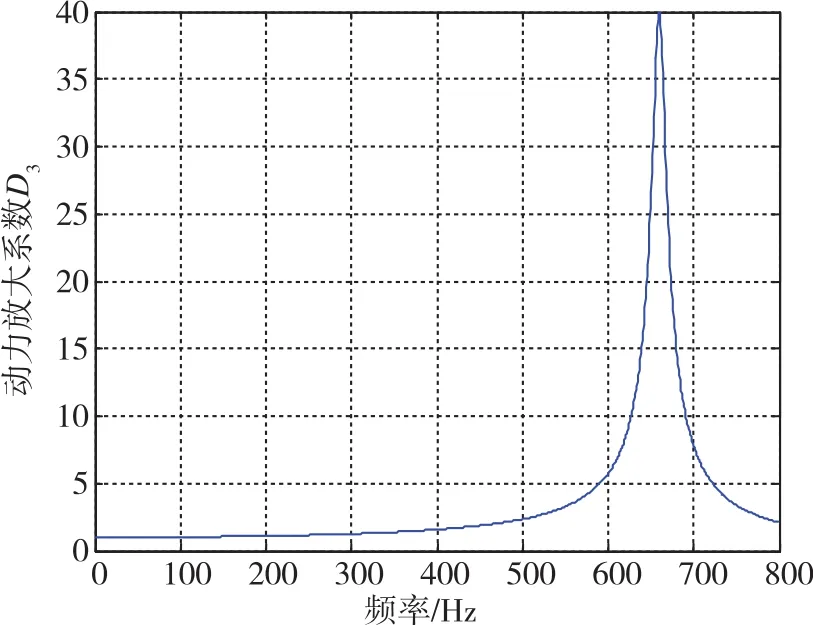
图7 三自由度系统I1和I2均设置较大值时得到的陀螺响应曲线Fig.7 Response curve of gyroscope when I1 and I2have large values

4 陀螺抖动激励下惯导结构参数对抖动效率的影响

抖动效率是指以陀螺抖动固有频率为载荷频率对陀螺抖动系统施加交变电压时的陀螺响应反馈电压幅与激励电压幅之比，即

陀螺抖动动力放大系数是载荷频率与陀螺抖动系统固有频率相同或接近时陀螺响应幅值与静载荷激励下陀螺响应的比值，即

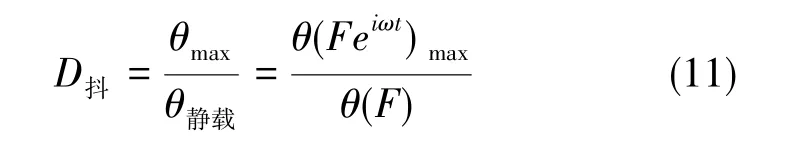
抖动效率与陀螺抖动动力放大系数都能够反应抖动系统输入与输出的关系，即在陀螺抖动动力系统中，动力放大系数大的系统抖动效率一定高。

图8～图15分别以陀螺抖动固有频率（图8）、陀螺抖轮安装阻尼（图9）、本体转动惯量（图10）、减振器刚度（图11）、减振器阻尼系数（图12）、箱体转动惯量（图13）、箱体刚度（图14）、箱体阻尼系数（图15）为变量考察陀螺抖动动力放大系数的变化情况。

图8 陀螺响应动力放大系数随陀螺抖频变化曲线Fig.8 Response curve of the gyroscope dynamic amplification factor with the dither frequency

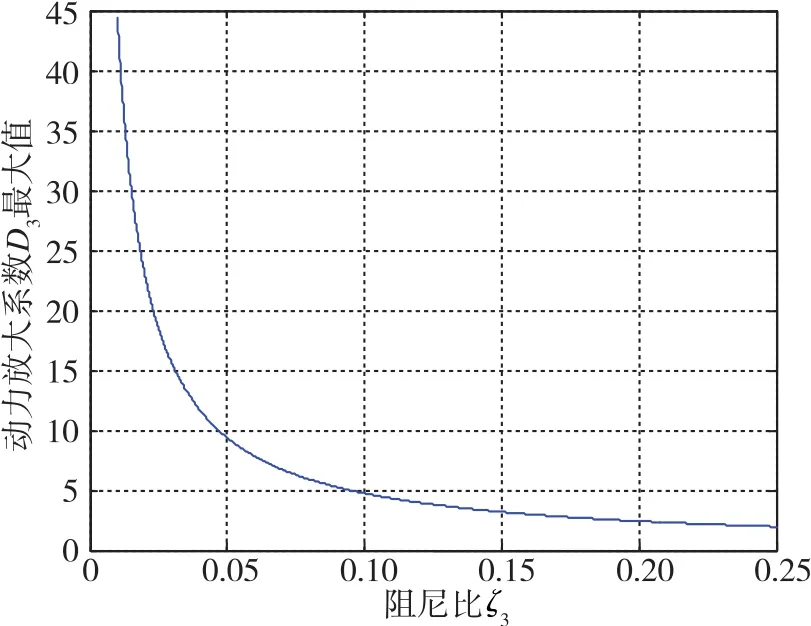
图9 陀螺响应动力放大系数随陀螺抖轮阻尼变化曲线Fig.9 Response curve of the gyroscope dynamic amplification factor with the dither mechanism damping

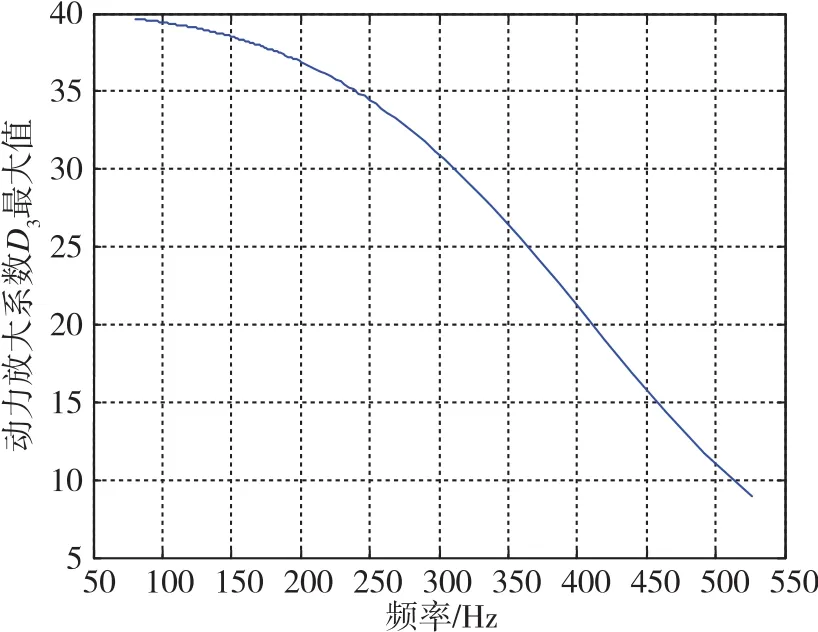
图10 陀螺响应动力放大系数随本体转动惯量变化曲线Fig.10 Response curve of the gyroscope dynamic amplification factor with the IMU rotational inertia

图11 陀螺响应动力放大系数随减振器刚度变化曲线Fig.11 Response curve of the gyroscope dynamic amplification factor with the absorber stiffness

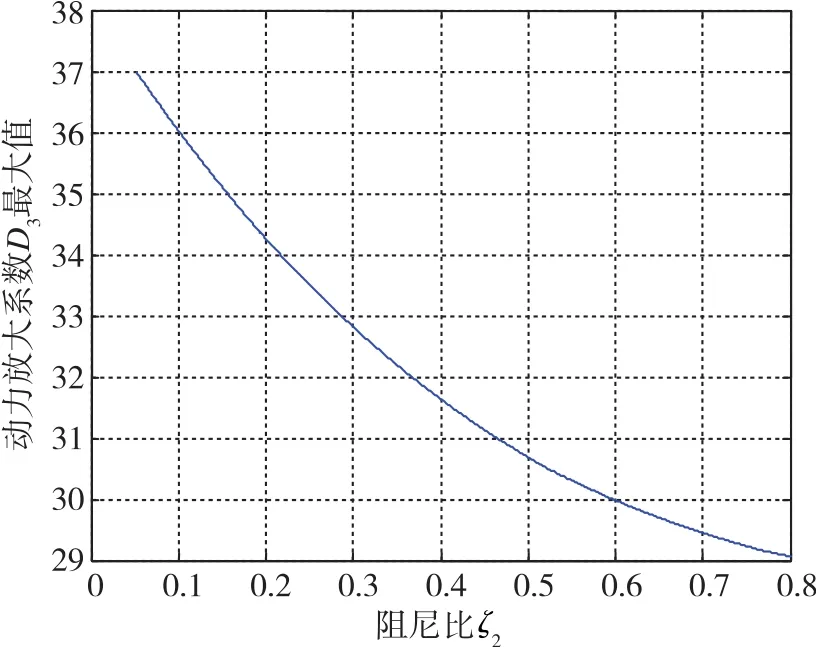
图12 陀螺响应动力放大系数随减振器阻尼变化曲线Fig.12 Response curve of the gyroscope dynamic amplification factor with the absorber damping

图13 陀螺响应动力放大系数随箱体转动惯量变化曲线Fig.13 Response curve of the gyroscope dynamic amplification factor with the shell rotational inertia

图14 陀螺响应动力放大系数随箱体结构刚度变化曲线Fig.14 Response curve of the gyroscope dynamic amplification factor with the shell stiffness

图15 陀螺响应动力放大系数随箱体阻尼变化曲线Fig.15 Response curve of the gyroscope dynamic amplification factor with the shell damping

由图8～图15可得到如下结论:

1）减振器刚度不变时，陀螺抖动动力放大系数随本体转动惯量增加而增大，动力放大系数在转动惯量量值较小的区间内可能发生急剧变化；

2）减振器固有频率不变时，陀螺抖动动力放大系数随本体转动惯量增加而增大；

3）本体转动惯量不变时，陀螺抖动动力放大系数随减振器刚度降低而增大；

4）在陀螺抖频不超过790Hz时，陀螺抖动动力放大系数随陀螺抖频增加而增大；

5）陀螺抖动动力放大系数随陀螺抖轮安装阻尼增加而减小，阻尼比在0～0.05的陀螺抖动动力放大系数可能发生急剧变化；

6）陀螺抖动动力放大系数随箱体刚度、阻尼、转动惯量的变化都不明显。

可见，在陀螺为选定型号的情况下，为了得到较大的陀螺抖动效率，应使得安装阻尼尽可能小，本体转动惯量尽可能大，减振器刚度尽可能小，同时应尽可能挑选抖频较大的陀螺。

5 陀螺抖动激励下惯导结构参数对测量精度的影响

软捷联激光惯导系统在线振动环境下可能引发惯性测量本体（IMU）发生伪圆锥运动，给测量带来误差[3，9]；在静载荷环境下，内部陀螺抖动激励同样可以引发惯性测量本体（IMU）发生伪圆锥运动[4]，给测量带来误差。可见，圆锥误差的大小与IMU的运动密切相关，尽量减小IMU的运动量级可以有效减小圆锥误差。

在前文所述三自由度模型中，考察本体的运动，可以揭示惯导结构参数对惯导测量精度的影响规律，有效指导设计。因此，仍对该模型进行仿真计算，得到了各结构参数对惯导测量精度的影响规律。

图16～图23分别以陀螺抖动固有频率（图16）、陀螺抖轮安装阻尼（图17）、本体转动惯量（图18）、减振器刚度（图19）、减振器阻尼系数（图20）、箱体转动惯量（图21）、箱体刚度（图22）、箱体阻尼系数（图23）为变量考察本体响应动力放大系数的变化情况。

图16 本体响应动力放大系数随陀螺抖频变化曲线Fig.16 Response curve of the IMU dynamic amplification factor with the dither frequency

图17 本体响应动力放大系数随陀螺抖轮阻尼变化曲线Fig.17 Response curve of the IMU dynamic amplification factor with the dither mechanism damping

图18 本体响应动力放大系数随本体转动惯量变化曲线Fig.18 Response curve of the IMU dynamic amplification factor with the IMU rotational inertia

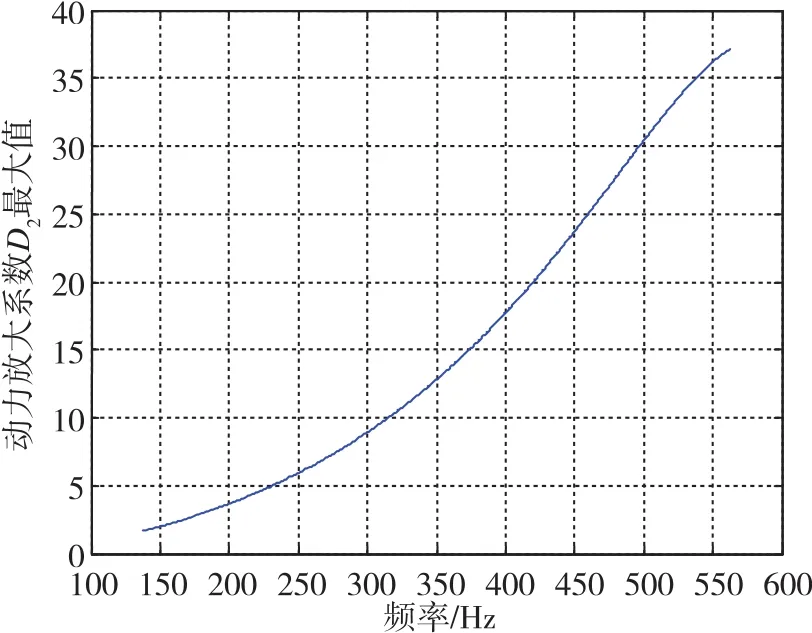
图19 本体响应动力放大系数随减振器刚度变化曲线Fig.19 Response curve of the IMU dynamic amplification factor with the absorber stiffness

图20 本体响应动力放大系数随减振器阻尼变化曲线Fig.20 Response curve of the IMU dynamic amplification factor with the absorber damping

图21 本体响应动力放大系数随箱体转动惯量变化曲线Fig.21 Response curve of the IMU dynamic amplification factor with the shell rotational inertia

图22 本体响应动力放大系数随箱体结构刚度变化曲线Fig.22 Response curve of the IMU dynamic amplification factor with the shell stiffness

图23 本体响应动力放大系数随箱体阻尼变化曲线Fig.23 Response curve of the IMU dynamic amplification factor with the shell damping

由图16～图23可得到如下结论:

1）减振器刚度不变时，本体响应动力放大系数随本体转动惯量增加而减小；

2）减振器固有频率不变时，本体响应动力放大系数随本体转动惯量增加而增大；

3）本体转动惯量不变时，本体响应动力放大系数随减振器刚度降低而减小；

4）本体响应动力放大系数随陀螺抖频增加而减小；

5）本体响应动力放大系数随减振器阻尼增加而减小；

6）本体响应动力放大系数随箱体刚度、阻尼、转动惯量的变化都不明显。

可见，在陀螺为选定型号的情况下，为了得到较小的本体响应，应使得本体转动惯量尽可能大，减振器刚度尽可能小，同时应尽可能挑选抖频较大的陀螺。获得较小的本体响应与得到较大的抖动效率的结论基本是一致的，但是需要注意陀螺安装阻尼的减小会同时增大本体的响应，在设计时需要综合考虑。如果陀螺抖动效率严重不足而本体响应较小，应考虑适当减小陀螺的安装阻尼。

6 结论

本文基于结构动力学理论对机抖激光捷联系统进行了三自由度动力学建模、解答和分析，分别得到了箱体转动惯量、箱体刚度、箱体阻尼、减振器刚度、减振器阻尼、本体转动惯量、陀螺抖频、陀螺安装阻尼对陀螺响应和本体响应的影响规律。其中，陀螺响应的大小反应了陀螺抖动效率的高低，本体响应的大小反应了圆锥误差的大小，与陀螺测量精度相关。基于上述规律，可以得到在陀螺为选定型号情况下激光惯导结构的动特性设计方法。

惯导结构参数设计应以以下原则为指导:

1）在满足质量要求的前提下，本体转动惯量应尽可能大；

2）在满足载体系统频率要求的情况下，减振器刚度应尽可能小；

3）在选定型号的陀螺中，应尽可能挑选抖频较大的陀螺；

4）陀螺安装阻尼的大小需结合实际情况设计，当陀螺抖动效率严重不足而本体响应较小时，应考虑适当减小陀螺的安装阻尼；

5）箱体的结构质量、刚度和阻尼在无外载荷激励条件下对陀螺抖动效率和本体响应的影响均较小，可据此适当进行减重设计。