浅谈大数据在精密惯性仪表中的应用

陈晓磊， 陈效真， 张福礼， 杨文超， 严小军

（1.超精密航天控制仪器技术实验室，北京100039；2.北京航天控制仪器研究所，北京100039）

0 引言

随着我国科学技术的进步和国防实力的提升，航天、航空、船舶和武器等运载器件对精密惯性仪表的性能、精度和可靠性均提出了更高的要求。摆脱传统的依靠人工装配核心功能组件的工艺手段，实现基于大数据的惯性仪表精密装配，是目前精密惯性仪表制造研究领域中的发展趋势。精密惯性仪表的核心零部件由多个精密微细结构构成，因此精密惯性器件的性能及可靠性主要取决于精密微细结构本身的制造性能，其精度和性能直接决定了高价值仪器设备和武器装备的核心战技指标。但是在我国，以精密微细结构为主要特征的高精度惯性仪表与发达国家相比还存在不小的差距。在多年的生产和科研过程中发现， “熵”理论工程大数据的解析演绎应用是解决精密微细结构大数据应用的重要方法，是提升高精度惯性器件性能的一种重要手段。在现阶段，重视产品生命过程测试试验、全制造流程数字量化应用，特别是全生命过程的数据采集和处理，是惯性仪表大数据制造亟需解决的问题。

本文以精密惯性仪表为研究对象，以其装配环节为例，分析了影响仪表精度及质量的问题，结合 “熵”理论在制造过程中的应用分析，提出了 “熵”理论在惯性仪表装配过程中的应用思路。最后，结合上述分析结果，以三维点云数字化虚拟装配技术在惯性仪表中的应用和 “熵”在惯性仪表故障识别与误差建模方向上的应用为例，给出了具体的研究内容、技术流程和研究结果。

1 精密惯性仪表

惯性仪表被广泛应用于地面武器、飞机、舰船、航天器中，其作用是敏感、测量载体加速度和姿态等信息，确定载体的运动轨迹参数，实现对载体的导航、定向定位。

1.1 精密微细结构

微细结构是指相对微小精细的结构或系统，复杂的零部件中常包含微小、微型、微细的结构系统。微细结构的介观尺寸是相对的，其无特定规定，但各有标准。精密结构体是指通过介观尺寸在优于原子直径≤10－10m量级经过精密超精密加工制造而得到的精致细密、精确周密的结构功能一体化部件，精密微细结构就是制造加工精度优于微米/亚微米量级、尺寸介于0.1mm至数个纳米（nm）之间的微小型精密结构。对于精密微细结构而言，它既是微细结构，又是精密结构体。从其内涵上而言，微细定当精密，精密必然微细。微细是精密的基础与必然，精密是微细的表象，两者之间相互作用、相辅相成。精密微细结构的价值主要体现在以下三个方面:

1）精密微细结构通常是高价值设备系统的核心和关键，更是武器装备精确打击的焦点和要害；

2）高价值仪器设备的精度与性能、精密武器装备的战标高度依赖于精密微细结构的精度与性能，与精密微细结构的制造有直接关系，特别是精密装配技术；

3）精密微细结构的形成过程和由多物理场、多应力耦合引起的时变附加误差具有时空演变特性，是影响和决定精密微细结构（件、体）及系统精度、性能和稳定性的极为重要的因素。

如图1所示，作为由精密微细结构（件）组成的典型产品，陀螺等精密惯性仪表是惯性导航系统的核心，其精度决定了整个系统70%以上的制导精度；再如将1kg载荷送入地球轨道，达到第一宇宙速度，需要1000KJ汽油燃烧所产生的能量。综上所述，精密微细即小型、轻质、高精度，是航天载荷和国防装备之根本。

图1 典型精密微细结构Fig.1 Diagram of typical precision microstructures

1.2 惯性仪表

如图2所示，惯性仪表是陀螺、加速度计等惯性测量装置的总称，被用于测量飞行器的角速度、加速度，建立基准坐标系，为初始对准提供方向基准、姿态及控制运动轨迹。惯性仪表具有自主、实时、隐蔽、抗干扰等显著优点，主要被应用于导航、测量、制导、定向、定位等领域[1-2]。惯性仪表主要是由精密微细结构的零部件和组件装配而成，因而惯性仪表的精度、寿命和可靠性直接影响着这些武器装备的最终性能指标，在武器装备中具有非常重要的地位，是决定武器装备精度和性能的重要核心器件，也是实现航空、航天、船舶、兵器等领域尖端武器装备性能的关键技术。例如，飞行时间为300s的远程导弹，其加速度计存在4×10－5的比例系数误差，射程误差为1km。

图2 典型精密惯性仪表Fig.2 Diagram of typical precision inertial instruments

2 大数据与制造

随着计算科学的飞速发展，大数据作为计算科学技术的发展产物，依托信息网络的全球化和云计算技术的广泛应用，也得到了快速发展。特别地，仿生工程、超材料、人工智能和机器人技术的仿真，极大地推动了工业技术的发展。随着现代制造技术的发展，制造过程的全流程数据已被开始采集并作为底层基础数据对制造全过程进行优化和迭代，大数据正在逐渐奠定现代制造和智能制造的基础，如图3所示。

图3 大数据发展内涵Fig.3 Diagram of big data development

2.1 大数据与工程大数据

制造过程中的大数据是指在精密微细结构体及系统形成、评价、应用、失效全生命周期过程中尽力获取的具有相关关联关系的数据集群，它具备一般大数据的五个特征:规模性（Volume）、高速性（Velocity）、 多样性（Variety）、 低价值密度（Value）和真实性（Veracity）[3]。 就制造过程大数据的内涵而言，它不是随机样本，而是全体数据；它不是精确具体数值，而是混杂集聚；它不是直接因果关系，而是存在相联关系，暗藏规律。除此之外，在制造过程中还存在工程大数据，它主要是指在实际工程应用中获得的数据，比如试验数据等。工程大数据的相对样本少，但具有潜在规律；数据无直接因果关系，但通过数据数理剖析、挖掘算法、智能优化等分析运算手段，可发现相应的影射规律和关系。总体而言，工程大数据是大数据的子集，含有一定的隐藏信息，可以指导用于整个过程的优化。综上所述，大数据应用是精密微细结构快速提升性能、深化机理、量化制造、确保可靠、有效补偿的创新工具和手段。

2.2 大数据制造存在的问题

我国的高精度惯性仪表作为典型精密微细结构，在精度、可靠性和寿命等方面距离世界先进水平仍有差距，问题在于全生命周期内的海量测试数据没有被充分挖掘、分析和应用，这严重制约了高精度惯性仪表中精密微细结构系统精度的提升、可靠性分析和生命预估的准确性。目前，存在的问题主要有以下几个方面[3]:

（1）数据采集

数据可信度差，与物理行为的映射关系不清。全生命周期内数据采集积累、统筹分析、系统协同应用管理、风险预测预判不力，行业壁垒严重，数据浪费现象严重。在现阶段，高精度惯性仪表在制造（特别是装配环节）上还没有完全实现自动化，这导致了很多过程数据无法被采集。

（2）数据管理

数据量大，采集与管理不匹配；数据类型多，缺乏统一管理。更新时效性差，交换难，利用率低，分析困难，处理与分析方法不规范，共享性差，自动判读深度、广度不够。在现阶段，专门面向惯性器件装配过程的数据库还不存在，因而对数据的合理管理也就无从谈起。

（3）数据应用

各阶段精度测试的指标体系不完善，概念不一致，行业应用存在差异。可靠性数据有限，小子样很难对系统性能进行有效估计。环境因素影响因子无法准确确定，缺乏系统失效判据，退役数据积累较少。高精度惯性产品的测试指标数据种类较多，但如何将数据分析应用到改进装配过程中，目前还没有成熟的应用案例。

2.3 惯性产品装配过程分析

随着科学技术的发展和国防装备对惯性产品精度和性能要求的进一步提升，惯性产品在生产的各个环节均需要进一步提升精度、稳定性与可靠性。特别是惯性产品的装配过程中，影响装配过程的因素过多，且一些影响产生的机理尚不明确，这些因素对惯性产品的精度、稳定性和合格率都产生了巨大的影响。如图4所示，随机过程随机因素、装配应力与变形、装配几何误差、装配洁净度、装配过程检测和装配的不确定性都是装配过程中的常见问题，这些问题均可直接或间接影响最后形成的惯性产品的精度和合格率。通过对典型惯性产品制造过程进行分析，可获悉装配工艺对产品精度和性能的贡献所占比例通常约为60%～80%。在现阶段，在典型的惯性产品装配过程中，装配过程随机因素、装配过程洁净程度这两个环节已得到了规范、有效且合理的控制。但是，由于对传统装配方式和部分环节缺乏定量的检测手段，剩余的四个环节，特别是由外部影响造成的零件或组件的应力变化，导致惯性仪表的精度、性能和可靠性无法达到国外先进水平。

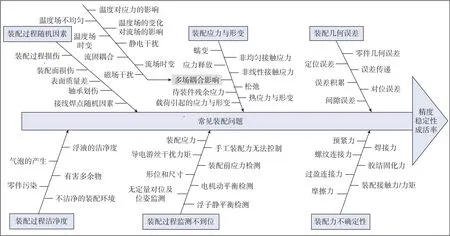
图4 典型惯性产品的装配过程分析Fig.4 Analysis of assembly process with typical inertial products

通过上述分析可知，影响惯性仪表装配过程的很多因素最终都会造成惯性仪表的零件或组件在装配过程中处于应力不平衡状态，而造成这种应力不平衡状态的原因主要是微观效应的产生，如图5所示。微观效应是指器件在经过精密超精密制造和集成过程后，即相关几何形位尺度在微米（10－6m）至纳米（10－9m）量级（即原子和分子尺度）时，工作原理将发生根本改变，进而所产生、呈现的各种场效应和互感、互溶、互阻等尺度效应的统称。

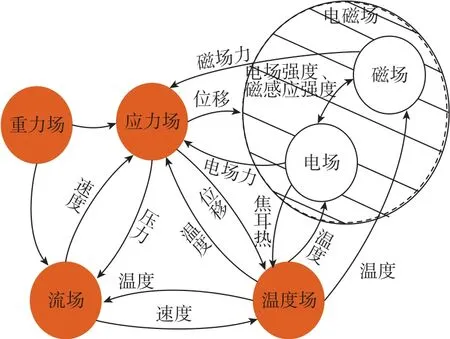
图5 各种物理场与应力场的相互关系Fig.5 Relationship between physical fields and stress fields

惯性仪表在装配过程中产生的典型微观效应如下:

（1）动态力矩引发的微观效应

①与g相关力矩引发的力不平衡效应；

②与g2相关力矩引发的力不平衡效应；

③与ω相关力矩引发的力不平衡效应。

（2）静态力矩引发的微观效应

①几何结构不对称引发的力不平衡效应；

②固有磨擦力矩引发的力不平衡效应；

③材料蠕变、塑变引发的力不平衡效应。

通过对上述微观效应进行分析可知，惯性仪表在装配过程中多种物理场的变化最终都会引发力不平衡，从而引起惯性仪表中零件或组件的应力变化。应力变化会造成惯性仪表中如质心稳定性等参数的变化，从而引起惯性仪表的误差。影响惯性仪表误差的因素有很多，但受限于现阶段我国传统的装配模式和有限的高精度测量手段，还无法准确建立基于多物理场耦合下的误差数学模型，并指导装配过程。因此，亟需将新的理论指导方法、误差数学模型等引入惯性产品装配过程，以满足未来武器装备系统对惯性产品精度、可靠性等指标的需求。

2.4 “熵”在惯性仪表制造过程中的分析

1850年，德国物理学家Clausius首次提出了“熵”的概念。1872年，Boltzmann提出 “熵”是系统失去 “信息”的度量，熵的获得意味着信息的丢失。系统的有序程度越高，熵越小，所含的信息量就越大，信息 “质”也越高；反之，系统的无序混乱程度越高，熵越大，信息 “质”和“量”越小，即信息和熵互补。由于这个概念的提出，越来越多的学者将 “熵”应用到了装配过程中的信息提取和评价体系中。美国Carnegie Mellon大学的Sanderson等[4]提出了零件熵的概念，分别采用 “熵”描述了装配过程中位置和方向的不确定性。哈尔滨工业大学的周亮等[5]依据信息熵的概念，采用信息分解转换法提取了装配信息，提出了装配信息熵并评价了零件间关联，求解了最小Hamilton回路问题，进行了最优装配序列求解。南京理工大学的周开俊等[6]提出了使用熵确定评价指标的权重，利用模糊综合评价对装配序列树模型的每层关系节点或子节点进行装配顺序优化，最终生成了优化装配序列。重庆大学的张根宝[7-8]和葛红玉[9]引入基于相对熵的多属性排序方法对各装配序列的质量进行了综合评价，提出了面向机械产品装配过程的装配质量缺陷源熵概念，通过计算权重和仿真分析，确定了缺陷源熵的可行性和有效性。合肥工业大学的马靖等[10]构建了IOT环境下的机械产品装配系统组态熵与互联熵的度量模型，提出了基于物联熵的机械产品装配系统复杂性的度量方法，最终通过物联熵的计算为物联网环境下的机械产品装配系统的设计、智能控制和优化等提供了有效的度量依据。北京理工大学的张发平等[11]建立了基于负熵固定点算法的加工误差分离模型，以某陀螺的某加工面加工误差分离为例，实现了相近尺度的系统加工误差分离。北京理工大学的张之敬等[12]提出了面向精密装配平面形状误差熵评价法和最大熵装配理论研究框架。针对 “熵”在惯性仪表上的应用，有研究学者提出以最大熵理论考虑陀螺装配体尺寸误差和形位误差传递。

通过对图6的大数据下精密微细结构制造网络图进行分析可知，“熵”理论可被应用于制造全过程的以下三个主要环节:1）几何熵模型，主要应用在设计-制造过程中的零件几何误差、三维结构几何误差和组件几何误差；2）以精密结构体集成设计为基础，通过对工艺流程进行量化，建立性能评价熵决策模型；3）建立在综合场作用下的精密微细结构体装配模型，通过仿真计算建立应力熵模型。最后，将上述三个环节通过人机协同技术有机集于一体，即形成了大数据下精密微细结构的全制造过程。

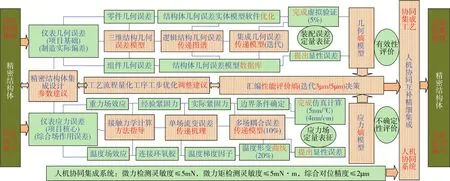
图6 大数据下精密微细结构制造网络图Fig.6 Network diagram of microstructure manufacturing based on big data

对于高精度惯性器件而言，零件加工精度越高，在加工误差中系统误差所占的比例越大。进一步从精密仪表内部应力、应变分布特征等微观角度分析误差分布规律，以 “熵”可作误差、应力定量与仪表装配精度的控制桥梁和数学工具，深入研究装配精度的定量控制。通过以上对国内外学者就 “熵”在制造过程中的应用分析，结合大数据下微细精密结构制造关系，“熵”在惯性仪表精密装配中的具体研究思路如下:

1）分析主要配合面的形位误差来源，建立误差模型，研究形位误差、装配误差及装配力作用下惯性器件在非均匀接触状态下的力学特性；

2）通过研究惯性产品在装配过程中温度场、流场、重力场与应力场的相互影响机理，探究多场耦合状态下应力场的形成与释放机理，及由其引起的几何误差和综合误差的传递规律与建模方法；

3）在误差建模与多场耦合应力场分析的基础上，建立高精度惯性器件微应力集成组装理论——最大熵装配理论模型；

4）基于最大熵装配理论，以关键零部件重要结合面应力、关键零部件装配误差等为优化参量，研究实现高精度惯性器件装配工艺的优化计算方法，实现高精度、微应力装配的工艺方法。

通过以上研究思路及内容，为实现高精度惯性器件微应力集成组装、提高惯性器件精度/一次装配合格率和稳定性提供理论和方法指导。

3 大数据与熵在惯性产品中的应用

3.1 基于三维点云的惯性仪表数字化虚拟装配技术

随着信息技术的发展，大数据已经越来越广泛地被应用于航空、汽车、船舶等行业的检测与数字化装配过程中。宋海涛等[13]针对复杂产品的装配服务执行决策问题，提出了一个大数据分析和调度优化模型。与此同时，还针对装配任务和内外部环境对装配效率的影响，提出了一种基于生理大数据的人为误差预测方法。孙汕民等[14]基于大量现场工艺决策需求和未来由大数据驱动的智能化装配线的发展趋势，对航空发动机装配仿真领域从装配结合面微观接触到复杂装配变形预测的物理级建模仿真问题以及研发工作进行了初步梳理和展望，并提出了若干建议。葛智君等[15]针对导弹生产装配环节批次零部件的选配工作，开展了基于流式大数据的弹装零部件优化选控相关技术和弹装流式大数据分析平台框架的研究。三维点云作为大数据建模的基础关键技术，已经在航空、汽车等机械制造领域获得了广泛的应用。但是，对于惯性仪表这类典型的精密微细结构体而言，由于技术在现阶段的局限性，大数据在惯性产品全制造过程（特别是装配环节）中的应用还处于初级阶段。

在现阶段，惯性仪表中关键的高精度装配环节是同轴装配，如动压气浮轴承球形偶件装配和静压液浮轴承偶件装配。目前，惯性仪表中的同轴装配技术还存在以下问题和不足:

1）从仪表性能出发，各电磁元件、零组件之间的同轴对位精度直接影响惯性仪表的三轴正交，这导致了输入轴对准误差、液浮磁悬浮支承耦合误差等；

2）从装配量化、微观匹配方面考虑，关键零件的检测效率低，未能全面反映配合面上影响装配精度的误差因素；

3）配合件之间的选配依赖人工技能，试装会损失加工精度。

在现阶段，对于尺寸偏大的零组件而言，同轴对位装配精度很难达到0.003mm的高精度要求。

上述同轴装配技术存在的问题，以及大数据在惯性产品中的实际应用和现阶段惯性仪表装配所面临的问题，可以通过开展基于三维点云的数字化虚拟同轴装配技术研究来实现解决。惯性仪表的微细结构特点和其中主要的研究内容，主要有以下几个方面:

（1）基于光学检测的点云形貌获取与重构技术

如图7所示，通过高精度光学检测手段，获取相关零件的形貌点云数据，利用三维点云重构算法构建数字模型，实现数字化装配，为后续智能选配、对位装配、关联分析提供依据。其中，主要的研究内容包括:

图7 点云模型重构流程Fig.7 Flowchart of point cloud remodeling

①基于高精度光学测量的点云形貌获取技术；

②基于精密光学三坐标的点云获取技术；

③基于多波长干涉原理的点云获取技术；

④点云重构算法研究；

⑤点云预处理技术研究；

⑥三角网格重构技术研究。

（2）高精度智能选配技术

智能选配技术通过对高精度三维点云数据进行特征识别，提取特征参数并建立特征参数数据库，对特征参数进行决策和评估。根据点云间的位置关系建立特征匹配原则，按照匹配原则进行智能选配，对选配成功的组件进行虚拟装配，验证装配结果，将装配结果指标反馈到实体上，从而指导装配机构进行工作。基于点云模型的智能选配流程图如图8所示，其中主要的研究内容包括:

图8 基于模型的智能选配流程Fig.8 Flowchart of intelligent selecting and assembly based on model

①特征数据库研究；

②匹配原则与模型的研究；

③智能快速选配方法研究；

④虚拟装配技术与迭代。

（3）精密装配多信息感知及同轴对位控制技术

图9所示为惯性仪表中力矩器座组件与壳体组件的装配系统构成。其中，视觉检测系统用于装配体的对中，力觉感知反馈系统用于控制装配过程中夹持力避免变形造成的装配误差。为了提高同轴对位精度和装配精度，主要的研究内容包括:

图9 精密装配系统的构成Fig.9 Constitution of precision assembly system

①视觉对位检测感知技术研究；

②力觉感知反馈调整技术研究；

③微力夹持及同轴装配技术研究。

（4）数据关联分析及应用技术

图10为仪表装配过程的数据关联图，可通过对图中仪表装配过程的数据进行分析，建立数据关联分析模型。以引起惯性仪表同轴装配精度超差、仪表故障或精度超差为目标，并将相关数据作为样本验证模型的关键数据，对模型进行验证与迭代，从而根据模型建立仪表装配数据与装配精度之间的内在规律。最后，通过这些内在规律对惯性仪表的零件重构模型和快速选配模型进行优化。在智能装配设备方面，主要可用于对同轴对位装配系统进行改进；在仪表精度方面，主要应用于提高磁悬浮对中精度和仪表零次项误差。

图10 装配过程的数据关联图Fig.10 Data connection diagram of assembly process

3.2 基于信息熵和随机漂移信号的陀螺故障智能检测

漂移误差是影响陀螺精度的主要因素，常值漂移具有时间累积效应，对陀螺的影响较大，但常值漂移属于系统漂移，可以通过改进设计工艺及建模补偿来降低。随机漂移量的大小与温度及振动等因素有关，反映了漂移误差的不确定性，是引起故障的重要因素。一般而言，陀螺故障可分为偏执故障、脉冲故障、漂移故障、周期故障以及尖峰故障。

可以利用信息熵对原始故障信号进行多层的小波包分解，并提取小波包能量熵[16]，然后构造信号的小波包特征向量，以此向量作为故障样本数据。使用上述大量样本数据对多层神经网络进行训练，以获得陀螺故障的诊断模型。

小波包能量熵为

式（1）中，N为原始信号长度，Hij为信号小波包分解的第i层第j个结点的小波包能量熵。

首先获取陀螺在不同故障类型下运行时的200组采样间隔为1ms的10s内的信号数据，然后根据小波包能量熵对数据进行计算处理，获得故障向量，如表1所示[17]。

表1 各种故障类型的小波包能量熵Table 1 Energy entropy of wavelet package in different fault types

通过对神经网络、样本数据和故障向量进行分析，选择输入节点为8、输出节点为5、隐节点为17的3层BP神经网络作为故障预测模型。使用180组数据作为训练样本，对神经网络进行训练，将其余20组数据作为测试样本。经过训练后的神经网络实际输出与理论输出如表2所示，证明了该模型具有有效性与准确性。

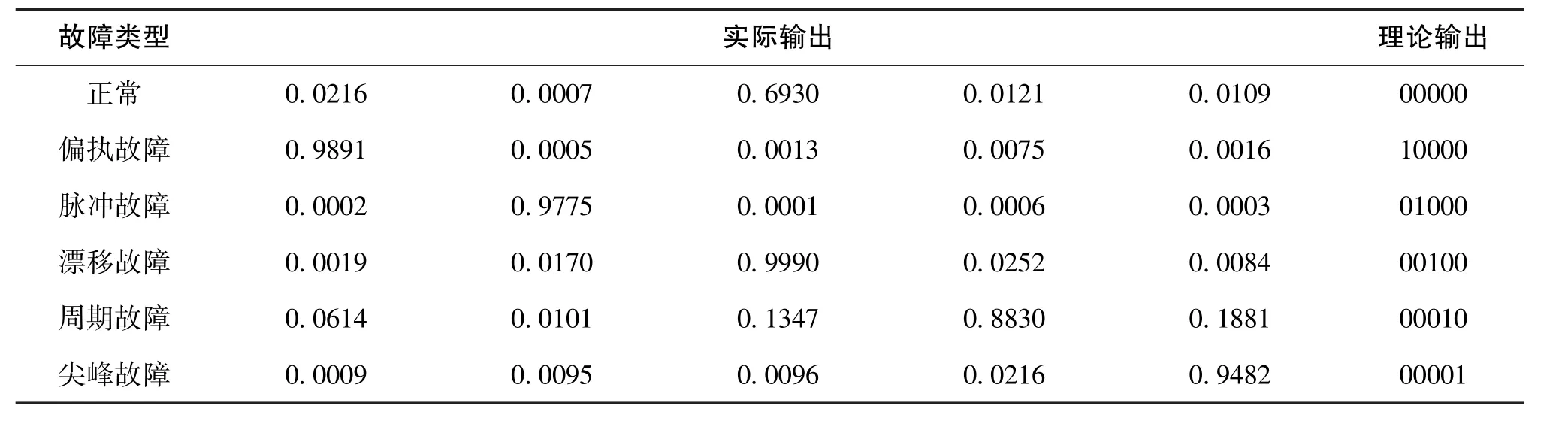
表2 神经网络故障诊断模型的实际输出与理论输出Table 2 Real and theoretical outputs of fault diagnosis model based on neural network

对一组尖峰故障下的陀螺随机信号进行处理和分析，得到的特征向量为[0.3695 0.3518 0.3689 0.3621 0.2725 0.3216 0.3845 0.3802]。将其作为神经网络输入向量，经过神经网络计算获得的实际输出向量为[0.0139 0.0042 0.0018 0.0003 0.9520]。通过与表2对比后可知，发生了尖峰故障。

3.3 基于样本熵的光纤陀螺温度漂移补偿模型建模

受环境温度的影响，光纤环内部的温度场总是不断变化的，这导致了光纤膨胀和折射率的不均匀，进而引起光纤环路中相向传播的光波产生非互易性相移[18]。温度对光纤陀螺的影响主要包括噪声和漂移，通过改进光学器件的性能或采取实时降噪方法[19]，可以减弱噪声的影响，而由漂移带来的影响常常需要通过建立补偿模型进行抑制。

利用有界噪声辅助的经验模态分解分析方法（Bounded Ensemble Empirical Mode Decomposition，BEEMD）[20]对陀螺型号进行自适应时域分解，将信号按频率和幅值依次分解为一系列的本征模态函数（Intrinsic Mode Function，IMF）。为了使特征分量的提取过程更为简单、具有较好的稳定性和一致性， 本文引入了样本熵（Sample Entropy， SE）[21]对BEEMD进行分解而得到的IMF进行分组和重构。利用上述重构数据对一种新型的单隐层前馈型神经网络极限学习机（Extreme Learning Machine，ELM）进行训练，获得累加多个分量模型的集成模型

以温变速率为±1℃/min、±5℃/min及±10℃/min的陀螺漂移输出与温度变化作为训练数据，以±8℃/min下的漂移输出和温度变化为测试数据。为了体现样本熵的引入对模型精度的提高，使用对比组数据对模型进行训练。一组数据不使用样本熵对上述数据进行BEEMD分解而得到的IMF进行分组和重构，而另一组数据使用样本熵。利用Matlab对两种模型进行训练，训练10次分别消耗0.699s和2.001s，对应模型的均方根误差分别为 1.43×10－2（°）/h 和 3.99×10－4（°）/h。 通过分别建立基于神经网络的经验模态分解分析方法（BEEMD-BP）、基于极限学习的经验模态分解分析方法（BEEMD-ELM）和基于极限学习的样本熵经验模态分解分析方法的模型（SE-BEEMD-ELM），对上述数据进行计算对比，对比结果如图11所示[22]。实验结果表明，在丧失一定速度优势的前提下，使用样本熵的建模方法在精度上比另一种小2个数量级，是一种有效的光纤陀螺温度漂移建模方法。

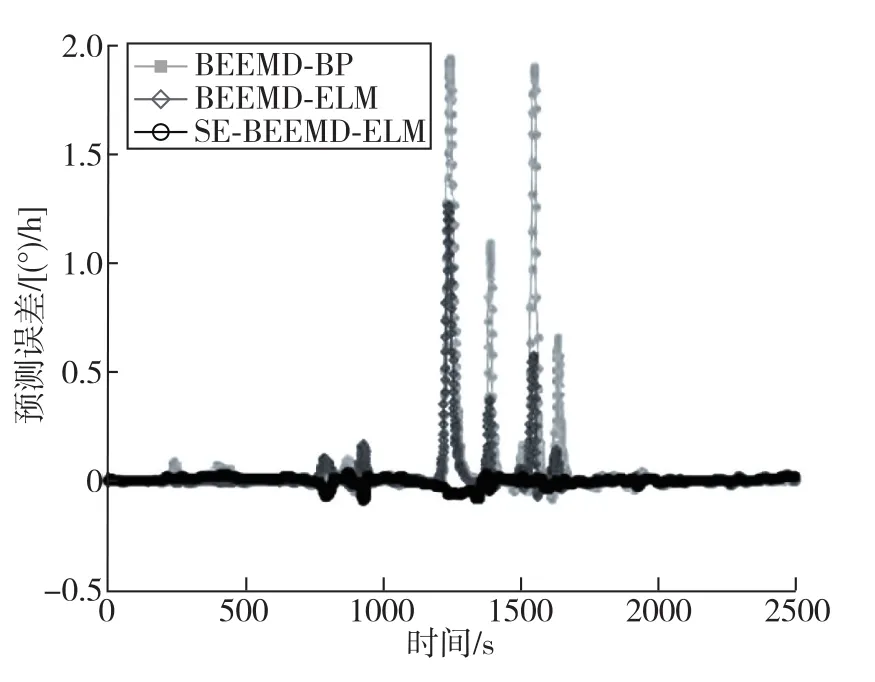
图11 不同模型的预测误差Fig.11 Prediction error of different models

4 结论

以复杂精密微细结构为典型结构的惯性技术产品，随着大数据技术的发展，对精度、寿命、可靠性、稳定性的要求越来越高，对体积、质量的要求却越来越小。由此，大数据技术成为了国防装备导航制导、稳姿、稳向的关键。微应力制造、微应力集成组装和误差补偿已成为惯性产品提高精度的瓶颈，因而必须充分利用全过程数据，结合新的数据分析与表征方法，建立 “数据孪生-孪生数据”，找到其中的关联规律，揭示制造过程中误差产生、应力形成及演变的机理和规律，提出微应力制造集成装配新思路，实现惯性技术应用精度的跨越，为提升新一代国防装配制造水平提供理论和方法基础。