沟通算理与算法以提高小学数学计算教学实效

吴燕妮

摘要：随着课程教学的改革，数学教学更注重培养学生的学习能力，发展学生思维。《义务教育数学课程标准（2011年版）》中，在各学段安排了四部分的课程内容：“数与代数”“图形与几何”“统计与概率”

“综合与实践”。运算不仅是数学课程中“数与代数”的重要内容，也与“图形与几何”“统计与概率”“综合与实践”有着密切的联系。数学运算是学生数学素养的重要组成部分。提升学生的运算能力，必须从数学课堂开始，夯实计算基础，提升数学素养。具体方法为利用沟通让知识形成链条，让旧知顺利迁移到新知;读懂算理，掌握算法，构建数学模型;沟通算理与算法，让学生从会算到巧算。

关键词：小学数学;计算教学;算理;算法

什么叫运算？根据一定的数学概念、法则和定理，由一些已知量通过计算得出确定结果的过程，称为运算。能依照一定的程序与步骤进行运算，叫做运算技能。不仅会根据法则、公式等正确地进行运算，并能理解运算的算理，能根据题目条件寻求正确的运算途径，称为运算能力。运算能力并非单一的数学能力，而是运算技能与逻辑思维等有机整合，既是一种操作能力，又是一种思维能力。算理和算法是提升运算能力的一体两翼，提升运算能力，从沟通开始。

一、沟通，让知识形成链条，让旧知顺利迁移到新知，提升学习能力

计算教学总是经历从理到法的过程，懂理才能让学生轻而易举地掌握法。纵观小学数学教材，与计算相关的内容，从10以内加减法作为教学起点，让学生感知认识相同计算单位相加减，为后面学习20以内进位加、退位减奠定基础。例如教学“9加几”，教材出现摆牛奶情景图、摆小棒，学生看到题目，可能根本不用摆拼小棒，不用看牛奶盒的情景图，很快就得出结果是13，较难入手分析算理。但当教师质疑：为什么是等于13？怎样看到10和3？简单的提问把学生的思维带回研究算理上来。为什么要研究算理？让学生为后面学习进位加法“哪一位相加满十要向前一位进一”找到依据。从而达到算理与算法的沟通，为学生学习新知识提供理论依据，让知识顺利迁移，提升学习能力。

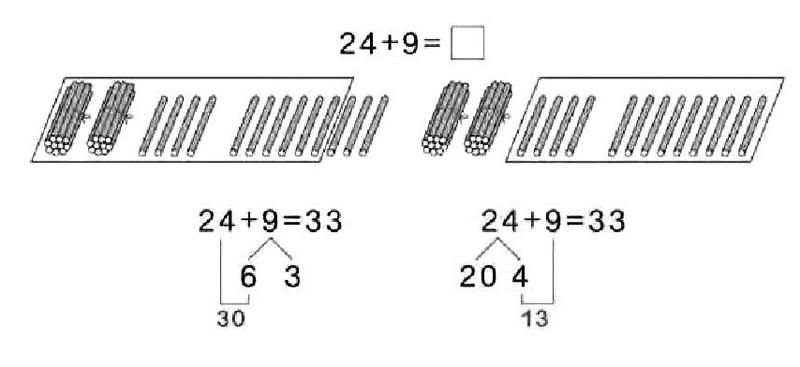
新知识往往是在已有知识的基础上发展的，在教学中，要善于唤起学生已有的知识基础和技能经验，为学习新知识提供着力点，通过类比、推理实现知识的迁移，形成完整的知识架构。如学习两位数加一位数24+9，先让学生摆小棒，明晰算理可以先算24+6，凑成30再加3等于33，也可以先算4+9=13，再用20+13=33。不管哪一种算法，都是以一位数加一位数进位加为基础，都用了凑整的思维。为后面学习多位数加减多位数做了铺垫。

二、读懂算理，掌握算法，构建数学模型

计算教学的目的是让学生掌握算法，形成技能。而在实际教学中，教学往往重视技能而忽略形成技能的过程，熟能生巧便成为计算教学常用的手法。传统的小学数学教学，大多数以讲授的方式把“计算原理”告诉学生，然后组织机械操练，重点培养学生的计算技能，最终的结果便是“为学计算而学计算”。怎样才能体现计算教学中的思维价值，让计算教学富有生命力？新课程背景下的计算教学在一定的现实（问题）背景下呈现例题，组织学生探究，为学生探究算法提供依据，达成让学生“在具体的情景中真正认识计算”的作用。学生进行探究，通过动手操作，如摆小棒、拨计算器、画线段图等活动，借助直观手段帮助学生理解算理，构建直观的计算模型，形成算法，让算理可视化，让算法合理化。如教学除数是两位数的除法——“92本连环画，每班30本，可以分给几个班？”借助小棒图的直观支持，理解“商为什么写在个位上”的问题，在摆小棒操作过程中，结合小棒图，让学生说出92里面有3个30，所以商3，同时呈现竖式的完整过程，突出30×3结果的书写位置，引导学生进一步理解算理。学生懂得算理，算法就有据可依。继而练习30÷10、40÷20、140÷20、280÷50，引导学生在练中说理，让学生用清楚、简洁、准确、流畅的语言说理。这样让学生进行说理训练，不仅能促进学生更好地理解算理算法，还能提高学生思维的自主性、灵活性和准确性。又如两位数乘一位数的笔算乘法16×8时，怎样理解算理满十进一？十位上的4是怎么得来的？通过摆小棒帮助学生理解算理，3个6相加得18，十位上便是3+1=4。通过简单的提问，让学生把算理和算法联系起来，这样，笔算乘法的模型便构建起来了。对于后面继续学习两位数乘两位数进位笔算乘法、三位数乘两位数进位笔算乘法便有据可依，算法便有所依托。

三、沟通算理与算法，让学生从会算到巧算，提升学习素养

在计算教学中，由于学生的知识背景和思维能力水平的差异，对同一个算式，不同学生可能会有不同的算法。有些题目可以运用不同的原理找到不同的简算方法。如120÷15，基本算法可以通过笔算计算出结果。新课程实验的课堂中，要求教师尊重学生的个性，鼓励学生大胆尝试。应用“一个数除以两位数，可以改成连续除以两个一位数”的规律，那么120÷15=120÷3÷5=40÷5=8;应用“被除数和除数同时扩大相同倍数，商不变”的规律，那么120÷15=（120×4）÷（15×4）=480÷60=8。通过优化算法体会掌握运算规律的优越性。然而，一题多种算法，并非适合所有计算的优化结果，这种优越性是在一定范圍内的。比如计算658÷47，盲目地应用规律，会加大计算的难度，反而适得其反。因此通过类别，基本算法的优越性便逐渐呈现。通过多种形式的练习、趣味练习，让学生动脑筋，想办法，形成解决问题必备的数学素养。计算不仅仅是纯粹的计算，更是一种解决问题的策略，把计算教学提升到数学素养的层次来组织教学，关注学生数学意识的培养必须成为计算教学的重要目标。

算理与算法是计算教学不可缺失的部分，在计算教学中，如果只讲算法，忽略算理，学生只能停留在机械记忆上;如果只停留在算理讲解，学生的计算能力没有得到很好的锻炼。因此，教师要根据知识呈现的顺序，在计算教学过程中合理地分配算理和算法的教学时间，重视算理与算法的沟通与联系，让学生形成技能，提升解决问题的能力，发展思维，提升数学核心素养。