基于Matlab的线性代数概念教学法的研究

杨丽萍

摘  要：线性代数课程是高校理工科学生的一门重要基础课程，具有概念多且抽象、课时少但应用广泛的特点。调研发现大部分学生学习效果不佳，仅记住几个概念、会简单的计算，认知层次和数学素养并没有提高。文章借助Matlab软件，提出针对概念教学的方法及策略。

关键词：行列式;线性方程组的解;线性变换;二次型

中图分类号：G640        文献标志码：A         文章编号：2096-000X（2020）03-0098-03

Abstract： Linear Algebra is an important basic course for college students of science and engineering. It has many abstract concepts and few class hours， but it is widely used. It is found that most of the students have poor learning effect. They only remember several concepts and can calculate simply， but their cognitive level and mathematical literacy have not been improved. This paper puts forward some methods and strategies for concept teaching with the help of MATLAB software.

Keywords： determinant; solution of linear equations; linear transformation; quadratic form

线性代数作为理工科学生的一门重要基础课程，一般都是大二第一学期开设，大多数理工院校都采用的教材是同济大学出版的，目前已经到第六版，多年来教材内容变化不大，但是授课学时变化很大，课时压缩势必会影响到教学。以我校为例，最初的46学时到现在的32学时，每周两次课，八周结束，这么少的学时没时间进行拓展和试验，另一方面，线性代数具有概念多且抽象、逻辑性强但应用广泛等特征，学生学习这门课有一定的难度[1]，大部分学生以考试为学习动机，采用记概念、背算式的学习方法，缺乏深度思考及抽象的思维能力和逻辑推理能力，更欠缺解决实际问题的能力，线性代数的基本概念在整个教学内容中占有重要位置[2]，概念的教学显得尤为重要，如何让学生从具体的概念中抽象逻辑推理是教学过程最关键的一环。对此，文章以概念教学为主线，提出了基于Matlab的线性代数概念教学法，就概念的几何意义、概念之间的关联以及概念的实际应用三个方面展开探讨。

一、注重概念的几何解释

借助Matlab软件加强二维和三维空间中重要概念的可视化讲授，使抽象概念更易于被学生接受，抽象就是抓住問题的本质属性，从简单几何概念抽象出复杂的代数概念，提升学生逻辑思维能力和逻辑推理能力。

（一）二、三阶行列式的几何意义

假设xoy平面上有两个向量=（a1， b1， 0），=（a2， b2， 0），则由向量积的定义，知×的大小是sin？兹，其中？兹为向量，的夹角。而由向量积的计算公式，有：

，

可见向量积×的大小也是二阶行列式a1 b1a2 b2的绝对值，即=sin？兹。因此由向量积的意义知，二阶行列式的绝对值在几何上表示该行列式的两个二维行（或列）向量所“张成”的平行四边形的面积，特别地，当二阶行列式等于零时，即平行四边形面积为零，说明此两向量不能“张成”平行四边形，此时的平行四边形退化为直线（即两向量共线），三阶行列式按第三行展开，有

由混合积的几何意义[3]知道，三个三维行向量组成的三阶行列式的绝对值在几何上表示由它们“张成”的平行六面体的体积，特别地，三阶行列式等于零时，此时平行六面体体积为零，说明三个向量不能“张成”平行六面体，即这个六面体退化为平面（直线），此时称三个向量共面（共线），更一般地，可引导学生推理n阶行列式的几何意义，完成从形象到抽象的过渡。

（二）线性方程解的几何意义

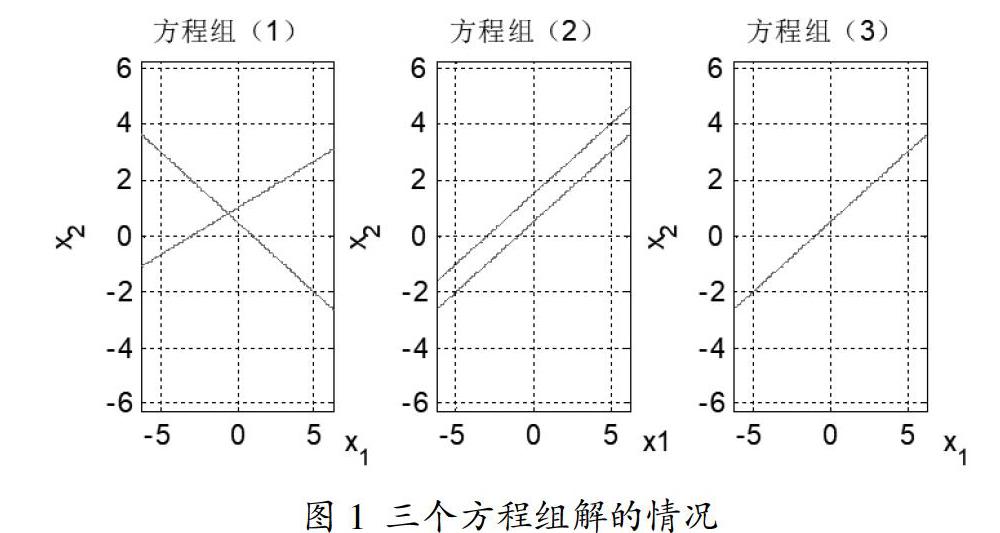
线性方程组求解问题是线性代数课程的核心内容，特别是方程组解的结构，一直是学生学习的一个重点更是难点。线性方程组的解不外乎三种情况：无解，唯一解和无穷多解，为了加深学生对问题的几何理解，通过Matlab软件中的ezplot命令画图（图1），展示二维（或三维）空间上二元（或三元）线性方程组解的情况。

例1 以下二元一次方程组解的情况

（1）           ;（2）            ;（3） ;

二元方程在平面上表示一条直线，方程组的解就是各直线的公共点，方程组（1）的两条直线仅有一个公共点，故有唯一解，方程组（2）的两条直线平行，没有交点，故无解，方程组（3）的两条直线重合，故有无穷多个解。

对于三元一次方程形成的方程组解的情况在空间解析几何中，平面与三元一次方程一一对应，m个三元一次方程组成的线性方程组解的情况可以用m个平面有无公共点来判别，解的个数就是公共点的个数。方程组有解，表明这m个平面有公共点。特别地，有唯一解时表示m个平面交于一点;有无穷多解且基础解系仅含一个解向量时，表示这些平面相交于一条直线;若基础解系含两个解向量，则表示这些平面重合。如果方程组无解，则表明平面没有公共点。有了低维空间上解的几何解释，再过渡到代数概念，对于更多元的线性方程组虽然不能想象出在高维空间内的几何图形，但是关于解的基本理论是一脉相承的。[4-5]

二、注重概念与其它学科的联系

注重不同概念间的联系，让学生体会到线性代数这门课程本身不是孤立的、而是更具开放性与延伸性，二次型是线性代数的重要概念之一，它起源于几何学中二次曲线方程和二次曲面方程化为标准形问题的研究。二次型的理论在物理学、几何学、概率论等学科中都已得到了广泛的应用。以往教师授课都是按照教材上强调怎么将二次型化为标准型及一个二次型判定是否正定，这样，学生学完后几乎不知道二次型有什么用，或者怎么用，因为这样授课完全与之前所学《高等数学》内容割裂开，学生获得的仅是一个新概念而已，而线性代数课程教学大纲要求先修课程是高等数学，即授课群体都需要有微积分知识的储备，如二次型概念就与高等数学中的二次曲面及多元函数最值关联紧密，讲授时不仅要使学生对二次型这个概念有更深层次的认识，更要拓宽认知结构。二次型化为标准型问题，大部分学生都会，但如果问该二次型等于常数时表示何种曲面，估计会有好多人不清楚，没思路，如果是在其标准型的基础上问表示何种曲面，这样启发引导，学生逐步揭示正确答案。

再如多元齐二次函数（二次型）在某条件下的最大值及最小值问题，常规解法是拉格朗日乘数法或化为无条件极值（如果条件本身复杂就不能化为无条件极值问题），对于拉格朗日乘数法需要求解含有多（变量个数加条件个数）个方程的方程组，求解过程很繁琐，用二次型求解思路是解出二次型对应矩阵的最大和最小的特征值，再结合瑞利定理即可。[6]

例2 求函数f=2x12+5x22+5x32+4x1x2-4x1x3-8x2x3，在条件x12+x22+x32=2下的最值。

在Matlab命令窗口先输入eig（A），得矩阵A的特征值;再输入最值命令函数就得到最大特征值10，最小特征值1。利用瑞利定理，有不等式：

学生思路清晰，繁琐计算让计算机来实现。这样快速得出最大值为20，最小值为2的结论，比较传统的笔算省时省力，准确度更高，同时也弥补了少学时的缺陷。

三、注重概念的实际应用

如果不考虑图像的颜色，只考虑图像的形状，则一个平面图像是由许多平面上点的一个集合，在平面上，一个点可以用一个二维数对表示，即平面上的每一个点都可以表示为一个二维列向量，因此平面图形可以看作是由许多点的位置构成的集合，即用一个矩阵的形式存储在计算机内存中。[7]在最简单的二维图形符号中，字母用于在屏幕上做标记，某些字母作为线框对象存储，对图形的操纵和显示用到的方法涉及到《线性代数》里的线性变换概念。

例3 在平面上有8个点，分别是

（0，0），（0.5，0），（0.5，6.42），（6，0），（6，8），（5.5，8），（5.5，1.58），（0，8），

由这8个点的坐标构成正体大写字母“N”的数据矩阵：

现在想将字母“N”改为斜体，将其各顶点向右平移其纵坐标的0.25个单位即可;而后再将斜体字变细，将其横坐标缩减为原来的0.75，这里实质上是描述了两个线性变换。由于线性变换与矩阵的一一对应关系，对应的变换矩阵分别是

和

令变换后的两种字体对应的数据矩阵分别是Y和Z，即有以下两线性变换：

为了更直观，在Matlab窗口中用plot命令画出字符变换前后的图形如图2。

这样设计计算机字库时，斜体或粗（细）体字库可以不必单独建立，只要对正体字库进行适当的线性变换，就可以实现斜体字、粗（细）体字等的变换，从而节约内存，线性代数中的概念在其他领域的应用实例还有很多，鉴于学时短，学生的专业不同，教师可以根据授课班级的具体实际选取应用实例讲解，采取布置课余大作业，让学生通过查资料、边学习边研究，任课教师以此作为平时成绩的考核依据。

四、结束语

文章阐述的概念教学法，主要从概念的几何意义、概念间的关联以及概念的实际应用三个方面阐述，选取的都是线性代数课程中的基本概念，任课教师对这些概念要挖掘它们的深层含义，引导学生追寻概念间的来龙去脉，把所学知识应用到实际生活中。鼓励学生自主思索、积极发现，提高数学素养，借助Matlab软件实现课程的多功能性，摒弃以考试为目标的功利主义，本着提高学生认知水平，拓展认知结构去教学，这样的教学才符合时代要求。

参考文献：

[1]Frank Uhlig. A New unified，bananced，and conceptual approach to teaching linear alagbra [J]. Linear Algebra and its Applications，2003，361：147-159.

[2]席政军.几何模型在线性代数教学中的应用[J].价值工程，2013，29：278-279.

[3]同濟大学数学系.高等数学下册（第7版）[M].北京：高等教育出版社，2014.

[4]肖汉光，邹雪，宋涛.MATLAB大学教程[M].北京：电子工业出版社，2016.

[5]杨威，高淑萍.线性代数机算与应用指导[M].西安：西安电子科技大学出版社，2009.

[6]陈怀琛，龚杰民.线性代数实践及MATLAB入门（第2版）[M].北京：电子工业出版社，2009.

[7]潘云鹤，董金祥，陈德人.计算机图形学原理、方法及应用[M].北京：电子工业出版社，2003.