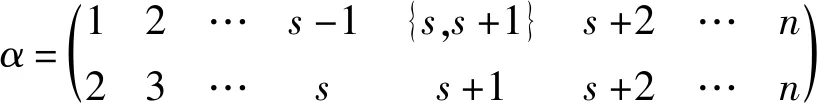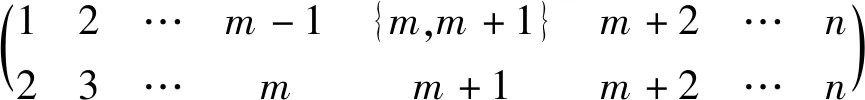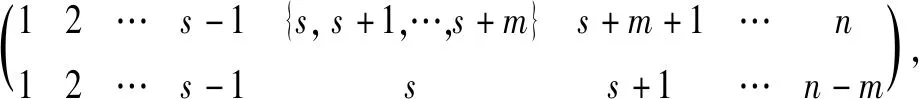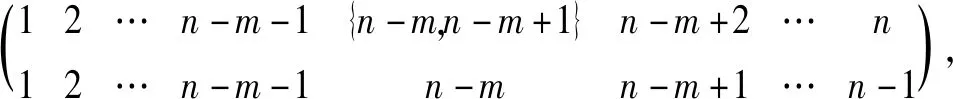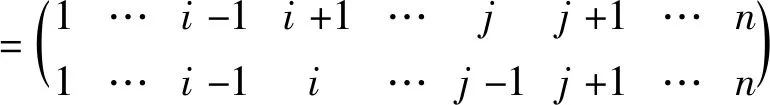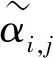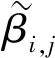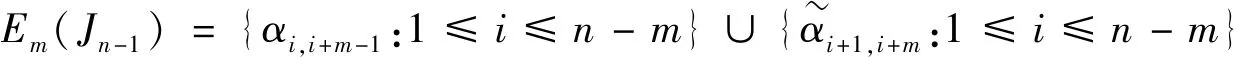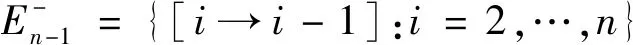半群POn的高次方准幂等元

吴江燕

(安顺学院 数理学院,贵州 安顺 561000)

0 引言

设[n]={1,2,…,n}并赋予自然序，Singn是[n]上的奇异变换半群。设α∈Singn，若对任意x,y∈[n],x≤y⟹xα≤yα，则称α是保序的。设On为Singn中的所有保序变换之集，则On是Singn的子半群，称On为保序变换半群。设POn为Singn中的所有保序部分变换之集，则POn=On∪{α:dom(α)⊂[n],(∀x,y∈dom(α))x≤y⟹xα≤yα}是Singn的一个子半群，称为保序部分变换半群。设α∈Singn，若α2=α，则称α是一个幂等元；若α2≠α且α2是幂等元(α4=α2)，则称α是一个平方幂等元；一般地，若αm≠αi(1≤i

通常，一个有限半群S的秩定义为：rankS=min{|A|:A⊆S,=S}。如果S由它的幂等元集E生成，那么S的幂等元秩定义为:idrankS=min{|A|:A⊆E,=S}。类似可以定义S的m次方准幂等元秩为:idrankmS=min{|A|:A⊆Em,=S}，其中Em为m次方准幂等元之集。显然有rankS≤idrankS且rankS≤idrankmS。对于有限变换半群秩的相关研究一直以来都是半群理论研究中的热点之一。1992年，Gomes和Howie[1]研究了On和POn的秩和幂等元秩；1994年，Garba[2]进一步分别研究了On和POn的理想L(n,r)={α∈On:|im(α)|≤r}和M(n,r)={α∈POn:|im(α)|≤r}(2≤r≤n-2)的秩和幂等元秩。1993年，Umar在文[3]中首次提出平方幂等元的概念，之后，对于有限半群中具有某种特殊性质的元素的秩开始被广泛研究。1999年，Madu[4]研究了有限变换半群的平方幂等元和平方幂零元；2001年，Madu[5]研究了保序链的有限变换半群中的平方幂等元；2013年，Imam[6]研究了有限变换半群中由平方幂等元生成的子半群。本文将考虑半群POn的顶端J- 类Jn-1中的m次方准幂等元，用集合

Em(Jn-1)={α∈Jn-1:α是m次方准幂等元}

本文未定义的术语及记法参见文献[7-8]。

1 主要结果及证明

据Gomes和Howie的结果，POn中的Green关系有如下刻画:

∀α,β∈POn,

[k,r]={α∈POn:|dom(α)|=k,|im(α)|=r}。

(i)Jn-1=[n,n-1]∪[n-1,n-1];

Lk={α∈Jn-1:im(α)=[n]{k}}。

R(k,k+1)={α∈[n,n-1]:α唯一的非单点核类为{k,k+1}}(1≤k≤n-1);

Ri={α∈[n-1,n-1]:dom(α)=[n]{i}}(1≤i≤n)。

设P,Q是[n]的非空子集，若对任意a∈P,b∈Q，有a

其中a1

定义设A⊆[n]非空，α∈POn，若对任意x,y∈A，有xα≠yα，则称A是α的部分横截集。

由部分横截集的定义易得如下引理:

引理1 设A⊆[n]非空，α∈POn，若集合A是α的部分横截集，则Aα=A。

引理2 设2≤r≤n-1，则[n,r]·[n,n-1]⊆[n,r]∪[n,n-1]。

证明任取α∈[n,r]，β∈[n,n-1]，则|im(α)|=r。

(i)若im(α)是β的部分横截集，则由引理1可得，

|im(αβ)|=|(im(α))β|=|im(α)|=r，

从而αβ∈[n,r]。

(ii)若im(α)不是β的部分横截集，则存在x,y∈im(α)，使得xβ=yβ。由β∈[n,n-1]可知，集合{x,y}是β唯一的非单点核类，于是集合[n]{x}是β的部分横截集，进而由部分横截集的定义易知，集合im(α){x}是β的部分横截集，从而

|im(αβ)|=|(im(α))β|=|(im(α){x})β|

=|im(α){x}|=|im(α)|-1=r-1。

综上所述，由α,β的任意性可得，[n,r]·[n,n-1]⊆[n,r]∪[n,n-1]。

引理3 设1≤s≤n-1， 则[n,n-1]s⊆[n,n-1]∪[n,n-2]∪…∪[n,n-s]。

证明用归纳法对s进行证明。

(i)当s=1时，显然有[n,n-1]⊆[n,n-1];

(ii)假设s=k时，结论成立，即

[n,n-1]k⊆[n,n-1]∪[n,n-2]∪…∪[n,n-k]。

当s=k+1时，由引理2及归纳假设可得,

[n,n-1]k+1=[n,n-1]k·[n,n-1]

⊆([n,n-1]∪[n,n-2]∪…∪[n,n-k])·[n,n-1]

=([n,n-1]·[n,n-1])∪([n,n-2]·

[n,n-1])∪…∪([n,n-k])·[n,n-1])

⊆([n,n-1]·[n,n-2])∪…∪([n,n-k])·

[n,n-k-1])

=[n,n-1]∪[n,n-2]∪…∪[n,n-k]∪[n,n-k-1]

综上所述，该引理成立。

定理4 设n≥3,2≤m≤n-1，令

其中a1

ak∉Ak,ak+1∉Ak+1,…,ak+m-2∉Ak+m-2。

证明由于Jn-1=[n,n-1]∪[n-1,n-1]，所以下面分两部分证明该定理:

(i) 当α∈[n,n-1]时，由引理3知

αm∈[n,n-1]∪[n,n-2]∪…∪[n,n-m]。

(1)

若存在唯一的k∈{1,2,…,n-m+1}，使得ak∉Ak,ak+1∉Ak+1,…,ak+m-2∉Ak+m-2，则由α的保序性可得，ai∈Ai,i≠k,k+1,…,k+m-2且ai∈Ai,i≠k,k+1,…,k+m-2或ak∈Ak+1,ak+1∉Ak+2,…,ak+m-2∉Ak+m-1。以下分两种情形讨论:

情形1 若ak∈Ak-1,ak+1∈Ak,…,ak+m-2∈Ak+m-3，则由α∈[n,n-1] 可得，Ak-1={ak-1,ak},Ak={ak+1},…,Ak+m-3={ak+m-2}。于是

αm=

从而αm≠α且(αm)2=αm，即α是m次方准幂等元。

情形2 若ak∈Ak+1,ak+1∈Ak+2,…,ak+m-2∈Ak+m-1，则由α∈[n,n-1]可得，Ak+1={ak},…,Ak+m-2={ak+m-3},Ak+m-1={ak+m-2,ak+m-1}，于是

αm=

从而αm≠α且(αm)2=αm，即α是m次方准幂等元。

反之，假设α是m次方准幂等元，我们将用反证法证明。

情形1 若a1∉A1,a2∉A2,…,am-1∉Am-1，注意到A1

我们断言s=m，若s≠m，则

αm=

从而(αm)2≠αm， 这与α是m次方准幂等元矛盾。由s=m可得,

α=

从而ak∈Ak,k=m,m+1,…,n-1。

情形2 若an-1∉An-1,an-2∉An-2,…,an-m+1∉An-m+1，注意到A1

α=

我们断言s=n-m，若s≠n-m，则

αm=

从而显然(αm)2≠αm，这与α是m次方准幂等元矛盾。

由s=n-m可得

α=

从而ak∈Ak,k=1,2,…,n-m。

情形3a1∈A1,a2∈A2,…,am-1∈Am-1且an-1∈An-1,an-2∈An-2,…,an-m+1∈An-m+1。若不存在k∈{m,m+1,…,n-m}，使得ak∉Ak,ak+1∉Ak+1,…,ak+m-2∉Ak+m-2，则ai∈Ai,1≤i≤n-1，从而α2=α，即α∈E(Jn-1)，这与α∈Jn-1E(Jn-1)矛盾。

假设存在k∈{m,m+1,…,n-m}，使得ak∉Ak,ak+1∉Ak+1,…,ak+m-2∉Ak+m-2且ai∈Ai,i

子情形3.1 若ak∈Ak-1,ak+1∈Ak,…,ak+m-2∈Ak+m-3，则由α∈[n,n-1]且ai∈Ai(i

Ak-1={ak-1,ak},Ak={ak+1},…,Ak+m-3={ak+m-2},|Ai|=1,i≠k-1,

于是由A1

a1=1,…,ak-2=k-2,ak-1=k-1,ak=k,ak+1=k+1,…,ak+m-2=k+m-2,

A1={1},…,Ak-2={k-2},Ak-1={k-1,k},

Ak={k+1},Ak+1={k+2},…,Ak+m-2={ak+m-1},…,An-2={n-1},An-1={n},

(2)

从而

α=

我们断言ak+m-1≠k+m-1。若ak+m-1=k+m-1,则{k-1,k,…,k+m-1}αm=k-1 且(k+m)αm=k+m-2,于是由α是m次方准幂等元可得,

(k+m)αm=(k+m)(αm)2=((k+m)αm)αm=(k+m-2)αm=k-1,

从而{k-1,k,…,k+m-1,k+m}αm=k-1。

因此αm∉[n,n-1]∪[n,n-2]∪…∪[n,n-m]，这与(1)矛盾。因此ak+m-1≠k+m-1。再由k+m-2=ak+m-2

子情形3.2 若ak∈Ak+1,ak+1∈Ak+2,…,ak+m-2∈Ak+m-1，则由A1k，从而由ak

ak=k+1,ak+1=k+2,…,an-1=n。

(3)

由A1

且k+1=ak∈Ak+1,k+2=ak+1∈Ak+2,…,k+m-1=ak+m-2∈Ak+m-1可得,

A1={1},…,Ak-1={k-1},Ak={k}。

(4)

再由ai∈Ai(i

a1=1,…,ak-1=k-1。

(5)

由A1

Ak+m-1={k+m-1},…,As-1={s-1},As={s,s+1},As+1={s+2},…,An-1={n},

(6)

从而由(3)～(5)可得,

α=

我们断言s=k+m-1。若s≠k+m-1，则s≥k+m，即s-m≥k，从而

{k+1,k+2,…,s-1,s,s+1}αm=s+1,kαm=s,于是由α是m次方准幂等元可得,

kαm=k(αm)2=(kαm)αm=sαm=s+1,从而{k+1,k+2,…,s-1,s,s+1}αm=s+1。因此αm∉[n,n-1]∪[n,n-2]∪…∪[n,n-m]，这与(1)矛盾。因此s=k+m-1。进而，由(3)，(6)可得，ai∈Ai,k+m-2

(ii) 当α∈[n-1,n-1]时，|Ai|=1,i=1,2,…,n-1。此时，定理可简单叙述为：α是m次方准幂等元的充要条件是存在唯一的k∈{1,2,…,n-m+1}，使得ak≠Ak,ak+1≠Ak+1,…,ak+m-2≠Ak+m-2。

类似(i)的方法即可证明(ii)。证毕。

设αi,j=

∈[n,n-1],i≤j;

∈[n,n-1],j≥i+1;

∈[n-1,n-1],i≤j;

∈[n-1,n-1],j≥i+1。

则据文献[1]可知,

定理5 设n≥3,2≤m≤n-1,Em(Jn-1)为Jn-1中的所有m次方准幂等元之集,则

Em(Jn-1)={αi,i+m-1:1≤i≤n-m}∪{αi+1,i+m:1≤i≤n-m}

∪{βi,i+m-2:1≤i≤n-m+1}∪{βi+1,i+m-1:1≤i≤n-m+1}。

证明由定理4易知,

αi,j是m次方准幂等元的充要条件是i+m-1=j且1≤i≤n-m;

βi,j是m次方准幂等元的充要条件是i+m-2=j且1≤i≤n-m+1;

定理6 设n≥3,2≤m≤n-1，则

|Em(Jn-1)|=4n-4m+2。

证明由定理5易知，

|Em(Jn-1)|=(n-m)+(n-m)+(n-m+1)+(n-m+1)=4n-4m+2。

注意到

[i→i-1]=αi-1,i-1,2≤i≤n;[i→i+1]=αi,i,1≤i≤n-1;

引理7[1]设n≥3，则POn=。

引理8[1]设n≥2，则rankPOn=2n-1。

(i)POn=〈Em(Jn-1〉;

(ii)idrankmPOn=rankPOn=2n-1。

(i)由定理5得,

因此,E(Jn-1)⊆。再由引理7可得,POn=。

(ii)显然，idrankmPOn≥rankPOn。于是由引理8可知，idrankmPOn≥2n-1。

令A={αi,i+m-1:1≤i≤n-m}∪{αi+1,i+m:1≤i≤m-1}

则A⊆Em(Jn-1)且|A|=2n-1。 易验证

[i+m-1→i+m-2]=[i+m-2→i+m-1][i+m-3→i+m-2]…[i+1→i+2]

因此，E(Jn-1)⊆〈A〉。由引理7可得，POn=〈A〉。故idrankmPOn=rankPOn=2n-1。证毕。