自回归误差下的改进Lyapounov最大指数法在短期负荷预测中的应用研究

苏 丽,吴 舰,吴 楠,乔玉鹏

(贵州师范大学 机械与电气工程学院，贵州 贵阳 550025)

0 引言

电力工业作为国民经济发展的基础产业，在社会经济发展建设中有着重要的地位。由于当前能源存储技术还不能够实现电能的大量存储，所以电网运行还必须满足发供电的平衡要求，而实现供需平衡的一个重要手段就是日前调度。而日前调度的依据是电网负荷量，因此对电网进行短期负荷预测就显得及其重要。随着智能电网逐步的建立与发展，负荷预测技术已经成为了电网智能化背景下的研究热点，传统的预测技术是利用时间序列之间的相关性来建立线性预测模型，如自回归模型、移动平均模型、自回归滑动平均模型等[1-3]，然而在实际的应用中所采集到的时间序列一般都是非线性的，例如电力负荷序列，若继续使用传统的线性预测模型将会导致预测精度下降。针对这一问题，通常采用非线性时间序列分析方法，采用相空间重构对非线性时间序列的电力负荷进行短期的预测，但求出来的短期电力负荷预测的误差较大，部分误差超过了规定的3%的允许值[4-5]，而预测的误差值过大，会对电网公司制定准确的发电机出力调度备用计划产生一定的影响，并且会造成相应的经济损失。此外，Knezevic等[9]的研究也发现采用传统的Lyapounov指数法进行短期的负荷预测的结果并不是很理想。

为了提高短期负荷预测效果且有效降低误差范围，通过多次的仿真及数据分析，最后发现预测的结果和嵌入维数的选取有较大的关联，在传统Lyapounov指数法预测中，嵌入维数的选取是根据人的主观意识来进行判断选取的，缺乏客观的模型对嵌入维数进行精确的定位，为了有效的解决这一问题，本文提出一种基于自回归误差算法的改进Lyapounov最大指数预测方法，来实现对嵌入维数的判定，以此来提高短期负荷预测的可靠性和准确性，通过对改进前后预测值的对比分析，发现采用本方法得到的短期负荷预测值最大误差有了明显的降低，所得预测数据也更加准确，同时也证明了该方法的可行性和有效性。

1 改进的Lyapounov最大指数法

电力负荷序列是一组非线性的时间序列，将混沌理论引入到非线性时间序列分析中，通过混沌相空间重构理论可以实现对电网负荷的短期预测[6-11]。在相空间重构中，延迟时间τ和嵌入维数m的适当选取对于重构具有重要的意义，很大程度上影响着负荷预测的误差范围。

1.1 延迟时间的求取

对延迟时间τ通常采用自相关法、互信息法、波动乘积法等进行求取，自相关函数方式是一种非常成熟的求取延迟时间τ的方法，由于对其求取具有简便性与实用性，故本文采用此法求取延迟时间，该法主要是对序列之间的线性相关性进行提取，对于连续的时间序列变量x(t),其自相关函数C(τ)表示为：

(1)

1.2 嵌入维数的求取

对嵌入维数m通常采用GP算法、Cao算法、C-C法等进行求取，因为Cao算法简捷、实用强且易于实现，故在本文中使用改进的Cao算法进行嵌入维数的计算。已知初始时间序列x1，x2，…，xn和延迟时间τ,可得出相空间矢量Xi，如下式所示；

Xi=(xi,xi+τ,…,xi+(d-1)τ),i=1,2,…,N

(2)

对于各嵌入维数下的最近邻点间的距离a(i,d)可表示为：

i=1,2,…,N-τ

(3)

其中，‖·‖表示为X上的范数，Xi(d+ 1)表示第i个重构相空间向量，此时嵌入维数为d+1，Xn(i,d)(d+1)表示在该状态下离Xi(d+ 1)最近的向量。

对于在相同嵌入维数条件下的距离变化平均值E(d)可表示为 ：

(4)

对比在嵌入维数发生变化的情况下的平均值E(d)的变化情况可表示为：

(5)

其中E1(d)表示平均值变化趋势，当E1(d)趋于稳定时即可确定最小嵌入维数m。

1.3 相空间重构

若存在时间序列x1，x2，…，xn，…，根据上述求得的延迟时间τ和嵌入维数m，则重构相空间可表示为:

(6)

取初始点为Y(t0)，寻找Y(t0)的最近邻点Y0(t0)，设L0为Y(t0)到Y0(t0)的距离，经过一定时间的演化后到达Y(t1)，寻找出与其相距最近的邻近点Y0(t1)，设L′=|Y(t1)-Y0(t1)|，当|L′|>ε时，保留点Y(t1)，并寻找另外一点Y1(t1),使L1=|Y(t1)-Y1(t1)|<ε，并满足其夹角小于45°，依次对上述过程进行迭代直至时间序列终点时刻结束，则Lyapounov最大指数λ为：

(7)

1.4 基于自回归误差算法的改进

采用传统的Lyapounov指数法下进行的短期负荷预测仿真结果的误差范围较大，很多预测结果都超出了允许的误差范围，这不仅会影响电力系统日前调度计划的准确性，而且还会造成相应的经济损失。传统的嵌入维数的选取是根据式(5)中E1(d)的波动变化由人为观察判断来确定，并没有根据模型对E1(d)参数变化值进行准确的计算，在由Cao算法得出的数组{e1,e2,e3,…,em,…,en}中，采用传统的主观判断法观察出来的嵌入维数为em，而从em+1到en的波动变化很小，在观测中往往被忽视掉而导致了结果的大误差出现，且在对嵌入维数进行取值时会由于观测者的主观判断不同导致有不同的误差存在，造成采用的最小嵌入维数预测的负荷误差具有随机性，这会使得预测的短期负荷值脱离实际值，造成日前电力调度计划制定的不准确，而采用误差均值可能会因为前面的波动过大影响精准度，为了解决上述问题，本文提出了一个基于自回归误差算法的改进Lyapounov最大指数算法，在原有的最大Lyapounov最大指数法的基础上对原Cao方法求嵌入维数进行了改进，从主观判断改进为采用偏离平方和作为指标对所得数据的离散程度进行判断比较，利用反向回归算法来保障嵌入维数求取的准确性，从而有效的降低预测最大误差程度，实现负荷预测的小误差高精度，其具体构造如下；

嵌入维数数组的总偏差平方和为

嵌入维数数组的回归平方和为

嵌入维数数组的残差平方和为

由上述条件可得到：

(8)

进一步化简为：

(9)

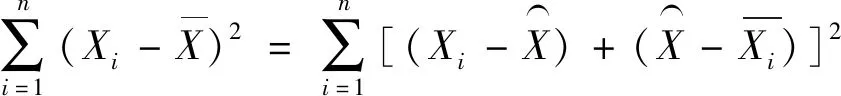
(10)

将其展开可表示为；

(11)

2 实例仿真及数据对比

图1 时间延迟与自相关函数的关系Fig.1 The relationship between time delay and autocorrelation function

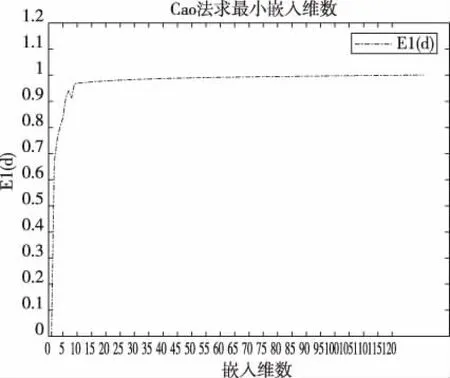
图2 嵌入维数与E1(d)的关系Fig.2 The relationship between embedding dimension and E1(d)

从图2中可以看出，若采取传统的主观判断法获得的嵌入维数m取值大概在8到12之间，由于个人的主观判断的不同，故分别对m取8、9、10、11、12进行负荷预测仿真，并与实际负荷数据进行比较，图3为数据之间的对比图；

图3 m取不同值时的预测数据Fig.3 m Prediction Data with Different Values

从图3中可以看出当m取值为8、9、10时，其预测值与实际数据的误差较大，当m取值为11、12时，误差开始有所降低。由此可以证明预测误差的大小与嵌入维数的取值有一定的关联，若根据传统的主观判断法来确定嵌入维数的取值需要进行多次反复的仿真和数据对比才能寻找出较佳的嵌入维数。而采用本文提出的偏离平方和对嵌入维数进行判断则能够快速简便的找出最佳的嵌入维数。由已求得的嵌入维数平均值变化趋势数组{e1,e2,e3,…,em,…,en},在Python的编译环境下可计算得出：

(12)

图4 仿真结果对比图Fig.4 Comparisons of simulation results

表1对改进前后Lyapounov指数法的短期负荷预测值与实际负荷值的误差进行了对比分析。采用的分析对比数据分别是最差的主观选取维数获得的预测值、最好的主观选取维数获得的预测值，以及采用误差均值获得的预测值和采用本文提出的算法得出维数获取的预测值。

表1 实际负荷值和短期预测负荷值Tab.1 Actual load value and short-term forecast load value

从表1中可以看出改进前主观最差维数和改进前主观最佳维数的预测误差也存在着一定的差异，由此可见根据观测者的主观判断进行取值是不科学的，采用误差均值作为判断指标比主观取值的预测效果有明显的进步，但稳定前的数据波动对取值的精准度有一定的影响，而采用本文提出的基于自回归误差算法改进后的短期负荷预测数值误差范围从主观预测误差的0～5.41%降到了0～2.6%，比采用误差均值法的预测优势更明显。此外，不仅最大误差有明显的降低而且误差范围也更加收敛，这大大的增加了预测值的可靠性和准确性，并且改进后的误差都在3%的允许误差范围内，满足了规定的短期负荷预测的误差要求。虽然在表1的误差结果中有部分预测优化值有雷同，部分优化值分别较明显，但是采用本文算法提出的误差范围明显缩小，这对电网的日前电量调度有着重要的意义，因为电量具有不可存储的特殊性，故预测误差范围的降低能够有效的解决因误差率导致的经济损失问题。该仿真结果不但证明了本文提出的观点，即嵌入维数的选取在一定程度上影响了负荷预测，同时也证明了所提出的改进Lyaponuov最大指数法预测方法对短期负荷预测的精准性，它可以有效的提高电力系统日前调度计划的可靠性和精准性，有助于电力系统的稳定运行。

3 结论

利用Lyapounov指数对混沌现象进行研究是较常见的方法之一，但是在对预测负荷的嵌入维数进行选取时，不合适的嵌入维数会导致预测的误差范围扩大，对短期负荷电量的预测的精准性会有较大的影响，本文提出了一种基于自回归平均误差算法的维数求取方法，该方法可以有效的解决由于传统采取人为主观对嵌入维数选取具有随机性问题。而且，通过对改进的Lyapounov最大指数算法，可以获得更加准确的嵌入维数，由此可以最大程度的解决因由于采用主观选择嵌入维数而导致的预测误差范围较大，预测数据可靠性不足的缺点。通过仿真对比显示，改进后的Lyapounov最大指数方法得到的预测误差范围更小，预测值可靠性更高，对电网负荷的预测值更加准确，为电网公司日前调度提供了更加可靠的数据支撑，有利于电网的安全稳定运行。