一类积分不等式组中未知函数的估计
黄星寿
(河池学院 数学与统计学院,广西 宜州 546300)
0 引言
Gronwall[1]和Bellman[2]为了研究微分方程的解对参数的连续依赖性考虑了下面的积分不等式

其中c≥0是常数,给出未知函数的估计式

因为Gronwall-Bellman型积分不等式及其推广形式在研究微分方程、积分方程和微分-积分方程解的存在性、有界性和唯一性等定性性质时具有重要作用,许多学者不断地研究它的各种推广形式,使其应用范围不断扩大,例如文献[3-8]。由于分析微分-积分方程组解的需要,人们经常研究积分不等式组。Greene[9]和Das[10]研究了积分不等式组


中未知函数的上界。该结果可以用来研究相应的积分-微分方程组的有关问题。Pachpatte[11]进一步研究了有趣的积分不等式组
(1)
(2)
中未知函数的上界。Kim[12]讨论了左边是未知函数幂函数的时滞积分不等式
周俊[13]研究了更一般形式的积分不等式组
(3)
(4)
作者受文献[9-13]的启发,研究了积分号外具有非常数因子,不等式左边是未知函数幂函数的时滞积分不等式组
(5)
(6)
不等式(5)和(6)把文献[11]中的不等式(1)和(2)推广成不等式左边是未知函数幂函数的积分不等式,把文献[13]中的不等式(3)和(4)推广成积分号外含有非常数因子的积分不等式。本文为了简化主要结果的证明,先引进两个引理,给出只含有一个未知函数的积分不等式中未知函数的估计。接着利用两个引理和变量替换技巧和放大技巧给出不等式组(5)和(6)中两个未知函数的估计。该结果可用于研究积分、微分方程组解的性质。
1 主要结果与证明
引理1[2,14]设u(t),g(t)为区间[t0,t1]上的非负实连续函数且导数g′(t)≥0,函数f(t)≥0在区间[t0,t1]上可积,它们满足

则

引理2 设v,a,b,c,f,g∈C([t0,t1],R+),a,b,c为不减函数,α(t),β(t)∈C1([t0,t1],[t0,t1])单调增并且在[t0,t1]上满足α(t)≤t,β(t)≤t,q>1为常数,它们满足不等式

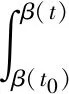
(7)
则不等式(7)中未知函数有估计式
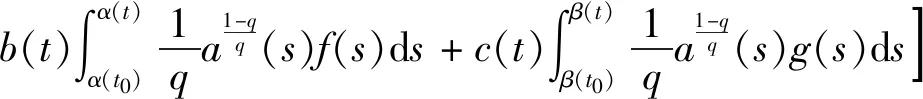
(8)
证明定义函数
g(s)v(s)ds,t∈[t0,t1]
(9)
利用Bernoulli不等式(1+x)a≤1+ax,其中0 (10) 把(10)代入(9)得到 (11) 其中T∈(t0,t1]任意选定,用不等式(11)的右端定义函数z2,即 由此可以看出z2(t)在(t0,T]上单调不减且有 (13) 求函数z2的导数,利用(11)得到 (14) 不等式(14)两边同除于z2(t)得到对任意t∈(t0,T],有 不等式(14)两边同时从t0到t关于积分t得到 t∈[t0,T] (15) 由(13)和(15)进一步有 z1(t)≤z2(t)≤exp (16) 令估计式(16)中t=T得到 z1(T)≤exp (17) 由于T∈(t0,∞)具有任意性,由(17)得到 z1(t)≤exp (18) 利用(12)和(18)得到v(t)的估计式(8)。 定理1 设u,v,a,b,g,h1,h2,h3,h4,∈C([t0,t1],R+),b,g为不减函数,α(t),β(t)∈C1([t0,t1],[t0,t1])单调增并且在[t0,t1]上满足α(t)≤t,β(t)≤t,p,q>1为常数,它们满足不等式(5)和(6),则有不等式(5)和(6)中未知函数的估计: (19) v(t)≤V(t),t∈[t0,t1] (20) 其中: (21) (22) (23) (24) 证明令 (25) 把(25)代入(5)得到 up(t)≤a(t)+g(t)z(t) 从而有 (26) 因p>1是一个常数,利用Bernoulli不等式,由(26)推出 (27) 把(27)代入(25)知道对任意t∈[t0,t1]有 (28) 利用引理1,由(28)推出对任意t∈[t0,t1]有 z(t)≤ (29) 把(29)代入(27)看出对任意t∈[t0,t1]有 (30) 其中:K1,K2在(23)和(24)中定义,把(30)代入(6)得到 (31) 其中:A(t),B(t)分别由(21)和(22)式定义,把引理2应用于不等式(31)推出所要求的估计式(20)。把估计式(20)代入不等式(30)得到所要求的估计式(19)。 考虑积分方程系统(参见[13]) (32) (33) 为了对x,y的模进行估计,令u(t)=‖x(t)‖,v(t)=‖y(t)‖,由(32)和(33)得到 M1是一个常数,故K1(t)有界。 M2是一个常数,故K2(t)有界。 综上,由定理1可以看出系统(32)和(33)的解的模有界。




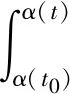


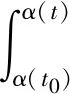
2 应用



