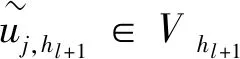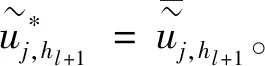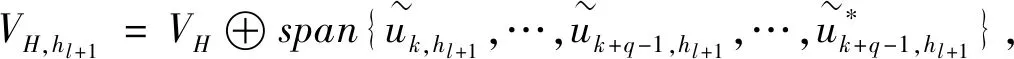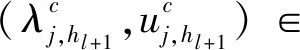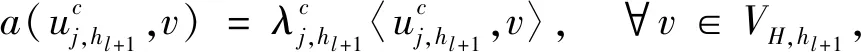反散射中Stekloff特征值问题的一个性质
杨一都,闭 海,张 宇
(贵州师范大学 数学科学学院,贵州 贵阳 550025)
0 引言
考虑下列反散射中的Stekloff特征值问题:
(1)

问题(1)是一个特征值参数出现在边界上的非自共轭特征值问题,且不满足一致椭圆条件,不能被二阶椭圆特征值问题的标准理论所覆盖。在2016年,Cakoni等[1]研究了该问题的数学性质,证明了它的特征值是Neumann-to-Dirichlet算子(紧算子)的特征值,并提出了它的变分公式和协调有限元逼近。在文献[1]工作的基础上,刘杰等[2]证明了有限元特征值的误差估计,闭海等[3]研究了二网格离散和局部有限元方案,张宇等[4]研究了多网格校正方案与自适应有限元法,杨一都等[5]研究非协调有限元逼近。
本文进一步研究问题(1)的数学性质。我们将证明相应(1)的共轭Stekloff特征值问题的i阶广义共轭特征向量是Stekloff特征值问题(1)的i阶广义特征向量的共轭。基于这一性质,我们改进现有文献中Stekloff特征值问题二网格离散方案[3]和多网格离散方案[4]。
1 Stekloff特征值问题及其共轭
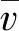
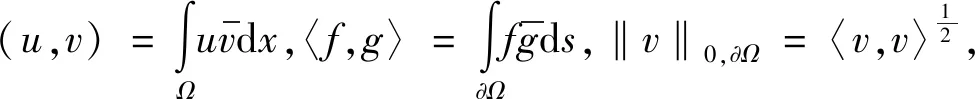
并定义连续半双线性型
a(u,v):=(▽u,▽v)-k2(nu,v), ∀u,v∈H1(Ω)。
为叙述简单起见,记λ=-μ。
(1)的变分公式是[1]:求(λ,u)∈C×H1(Ω),u≠0,使得
a(u,v)=λ〈u,v〉, ∀v∈H1(Ω)。
(2)
设{πh}是Ω的形状正规网格族[7],h是πh的网格直径,Vh⊂H1(Ω)是定义在πh上的分片m(m≥1)次多项式空间。
问题(1)的有限元近似是:求(λh,uh)∈C×Vh,uh≠0,使得
a(uh,vh)=λh〈uh,vh〉, ∀vh∈Vh。
(3)
与原特征值问题(2)或(1)相应的共轭特征值问题是:求(λ*,u*)∈C×H1(Ω),u*≠0,使得
(4)
(5)
对特征值问题(2)相应的边值问题定义解算子A:H1(Ω) →H1(Ω)满足
a(Af,v)=〈f,v〉, ∀v∈H1(Ω)。
(6)
由(2)和(6)得
a(u,v)=a(λAu,v),∀v∈H1(Ω)
则问题(2)有等价算子形式:
Au=λ-1u。
(7)
对问题(3)相应的方程定义解算子Ah:H1(Ω)→Vh满足
a(Ahf,v)=〈f,v〉, ∀v∈Vh。
(8)
由(3)和(8)得
a(uh,v)=a(λhAhuh,v),∀v∈Vh,
则问题(3)有等价的算子形式:
(9)
称使得N((λ-1-A)α)=N((λ-1-A)α+1)的最小正整数α为λ-1-A的陡度,这里N表示零空间。称q=dimN((λ-1-A)α)为λ的代数重数。

在文献[7]中683页及693页讨论了广义特征向量的阶:称使得下式成立的最小整数i为算子A的相应于λ的广义特征向量u的阶:
(A-λ-1)iu=0。
(10)
显然,1阶广义特征向量就是特征向量。ui是i(i>1)阶广义特征向量的充分必要条件是存在i-1阶广义特征向量ui-1满足
a(ui,v)=λ〈ui,v〉+λa(ui-1,v), ∀v∈H1(Ω)。
(11)
为方便阅读,下面给出证明:如果存在i-1阶广义特征向量ui-1使得(11)成立,则根据A的定义,有
a(ui,v)=λa(Aui,v)+λa(ui-1,v), ∀v∈H1(Ω),
于是
(λ-1-A)ui=ui-1,
因此,就有
(λ-1-A)iui=(λ-1-A)i-1ui-1=0,
即(10)成立。
反之,若ui是i阶广义特征向量,则(λ-1-A)ui是i-1阶广义特征向量,表示为
(λ-1-A)ui=ui-1。
据此我们推出
a((λ-1-A)ui,v)=a(ui-1,v), ∀v∈H1(Ω),
进而
a(ui,v)=λa(Aui,v)+λa(ui-1,v), ∀v∈H1(Ω),
a(ui,v)=λ〈ui,v〉+λa(ui-1,v), ∀v∈H1(Ω)
即(11)成立。
称使得下式成立的最小正整数i为算子Ah的相应于λh的广义特征向量uh的阶:
(12)
(13)
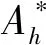
A*的相应于λ*的i阶广义特征向量u*i满足
(14)
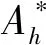
(15)
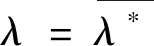
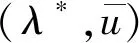
证明因为(λ,u)是(2)的第j个特征对,所以
a(u,v)=λ〈u,v〉, ∀v∈H1(Ω)。
(16)
根据a(·,·)和内积的定义可得
将上述两个式子代入(16),得到
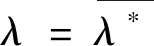
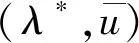
由于(λh,uh)是(3)的第j个特征对,所以
a(uh,v)=λh〈uh,v〉, ∀v∈Vh。
(17)
根据a(·,·)和内积的定义可得
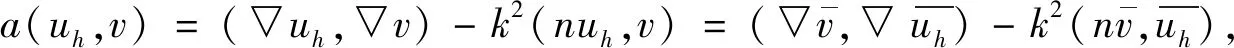
将上述两个式子代入(17),得
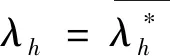

□
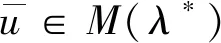

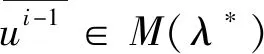
因为ui∈M(λ)是i阶广义特征向量,所以
a(ui,v)=λ〈ui,v〉+λa(ui-1,v), ∀v∈H1(Ω)。
(18)
根据a(·,·)和内积的定义可得
a(ui,v)=(▽ui,▽v)-k2(nui,v)
将上述3个式子代入(18),得
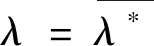
(19)
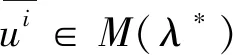
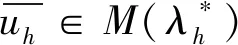
定理2表明
对一般的非自共轭特征值问题,在构造多网格离散、自适应方法等高效计算格式时,通常需要计算原特征值问题及其共轭问题。对问题(1),基于定理1和2,我们只需解原特征值问题,从而减少了计算量,进一步提高了计算方法的效率。
2 应用
特征值问题的二网格和多网格离散方法是一个备受关注的重要课题(见文献[9-14]等)。对于Stekloff特征值问题(1),闭海等提出了二网格离散[3],张宇等提出了多网格校正方案[4]。基于定理1和定理2,我们可以对文献[3,4]中建立的的计算方法进行改进。
2.1 Stekloff特征值问题的二网格离散
许进超[9]对特征值问题建立了基于反迭代的二网格方案。闭海等[3]成功地将其应用到Stekloff特征值问题(1)。基于定理1和定理2,本小节对文献[3]中二网格方案进行改进,提出求解Stekloff特征值问题(1)的两种新的二网格离散。
二网格方案Ⅰ
步1 在粗网格πH上解(3):求(λH,uH)∈C×VH,uH≠0使得
a(uH,v)=λH〈uH,v〉, ∀v∈VH。
步2 在细网格πh(h a(uh,v)=λH〈uH,v〉, ∀v∈Vh; 步3计算广义Rayleigh商 二网格方案II 步1 与方案I的步1相同。 步2 在细网格πh(h (▽uh,▽v)+(uh,v)=λH〈uH,v〉+((k2n+1)uH,v), ∀v∈Vh; 步3 计算广义Rayleigh商 文献[3]中方案1和2需要解原特征值问题和共轭特征值问题,而本文中二网格方案I和II只需要求解原特征值问题,且明显地,当λ是单特征时,文献[3] 中定理4.1和4.2仍然成立。 基于多水平校正,林群和谢和虎[11]建立了一种新型多网格方案,并且它被张宇等[4]成功应用到Stekloff特征值问题(1)。基于定理1和定理2,本节对文献[4]中多网格校正方案进行改进。 首先,给定初始网格πh1=πH。通过正规方法对πh1加密得到三角形网格序列{πhl},并且 这里ξ是一个整数。 基于该网格序列,定义如下线性协调有限元空间(m=1): VH=Vh1⊂Vh2⊂…⊂Vhn⊂H1(Ω)。 定义 一步校正 步2 定义新的有限元空间: 将上述两步表示为 现在,我们使用上述校正步建立(1)的多网格校正方案。 多网格校正方案 步1 对j=k,…,k+q-1,在粗网格πH上解(3): 求(λj,H,uj,H)∈C×VH使得‖uj,H‖0,∂Ω=1且 a(uj,H,v)=λj,H〈uj,H,v〉, ∀v∈VH, 步2 对l=1,2,…,n-1, 结束。 文献[4]中方案4.1需解原特征值问题及共轭特征值问题,而本文中多网格校正方案仅需要解原特征值问题,且易知文献[4]中定理4.1仍然成立。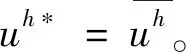
2.2 Stekloff特征值问题的多网格校正方案