2019年高考课标卷Ⅲ理科第21题的推广
2020-01-10 06:39:08贵州师范大学数学科学学院550001
中学数学研究(江西) 2019年12期
贵州师范大学数学科学学院 (550001) 姜 文
2019年高考课标卷Ⅲ以全国教育大会精神为指导,认真贯彻“五育并举”方针,落实立德树人根本任务,突出数学学科特色,着重考查学生的理性思维能力,综合运用数学思维方法分析问题、解决问题的能力.试题突出数学学科核心素养导向,注重能力的考查,综合性和实用性较强.整套试题注重融入数学文化,以反映我国社会主义建设的成果和优秀传统文化的真实情境为载体,贴近学生生活,联系实际,在评价中引导数学教育落实“立德树人”的根本任务.其中,理科21题是一道质量较高的试题,它主要考查学生直观想象、逻辑推理和数学运算等核心素养,考查学生综合运用数学知识解决问题的能力,难度适中.本文研究该题第(1)小题.
1.试题呈现

(1)证明:直线AB过定点;

2.试题解答
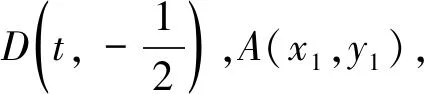
(2)略.
3.研究与推广
该题第(1)小题告诉我们一个事实,即过抛物线的准线上的任意一点作抛物线的切线,切点所在的直线恒过该抛物线的焦点.这是偶然还是必然?如果是必然,那么椭圆和双曲线是否也有类似的结论呢?笔者对此作了研究,得到如下性质.
性质1 过抛物线C:x2=2py(p≠0)的准线上的任意一点作抛物线的两条切线,切点分别为A,B,则直线AB恒过C的焦点.
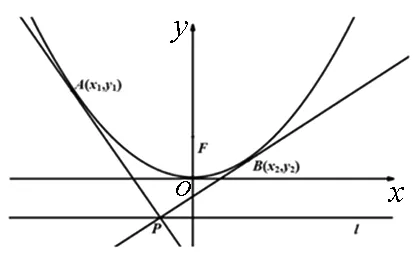
图1
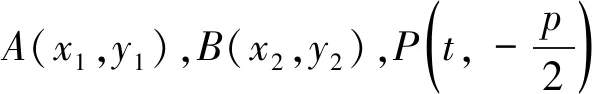
圆锥曲线往往有对偶的性质,对于椭圆和双曲线,也有如下的性质.
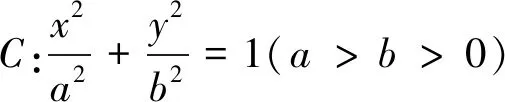
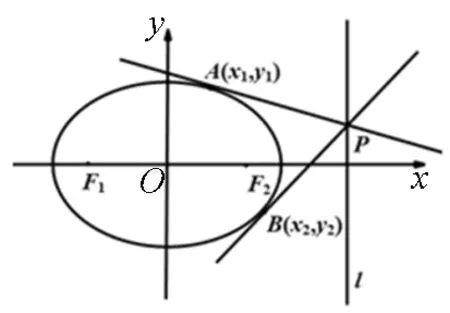
图2
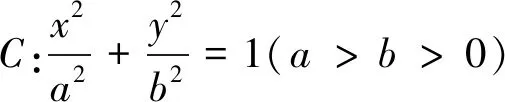
同理可知,若P为左准线上的任意一点,则直线AB恒过左焦点F1(-c,0).命题得证.


同理可知,若P为左准线上的任意一点,则直线AB恒过C的左焦点F1(-c,0).命题得证.
类似地,焦点在x轴上的抛物线、焦点在y轴上的椭圆和双曲线也有相同的结论,有兴趣的读者可以自证.
猜你喜欢
中学数学研究(江西)(2022年5期)2022-05-08 04:31:06
中学生数理化(高中版.高考数学)(2020年12期)2021-01-13 09:12:16
中等数学(2018年7期)2018-11-10 03:29:04
中学生数理化(高中版.高二数学)(2017年1期)2017-04-16 05:33:43
高中生·天天向上(2016年8期)2016-11-22 09:22:46
福建中学数学(2016年4期)2016-10-19 05:09:02
中学数学杂志(2015年9期)2015-01-01 09:00:16
淮北师范大学学报(自然科学版)(2014年4期)2014-07-04 06:21:46
福建中学数学(2013年1期)2013-03-06 01:46:00
数理化学习·高一二版(2009年2期)2009-03-30 05:02:56

