圆锥曲线两垂直切线的交点轨迹探究
2020-01-10 06:38安徽省合肥市第一中学230601谷留明
中学数学研究(江西) 2019年12期
安徽省合肥市第一中学 (230601) 谷留明
笔者在研究圆锥曲线准线上一点向该圆锥曲线引两条切线的过程中,得到结论:该点与相应焦点的连线垂直切点弦于相应焦点.与此同时注意到,对于抛物线,这两条切线恒垂直;而对于其他圆锥曲线,这两条切线不一定垂直.本文探讨对于圆锥曲线,能向该圆锥曲线引两条相互垂直的切线的动点轨迹问题.
定理1 若过一动点能向某抛物线引两条相互垂直的切线,则该动点的轨迹为该抛物线的准线.
证明:不妨设抛物线C:y2=2px(p>0),如图1.
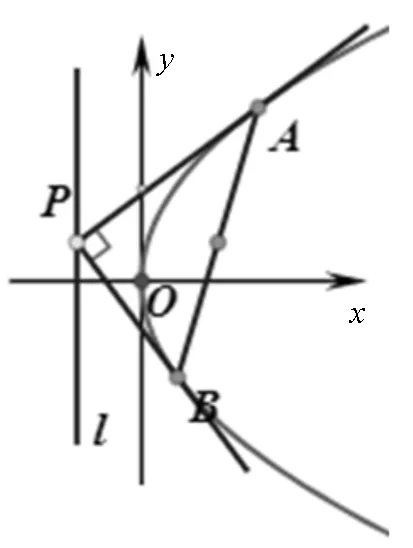
图1
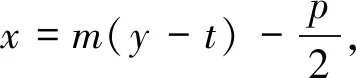
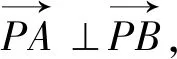
那么,若过一动点能向其他圆锥曲线引两条相互垂直的切线,则该动点的轨迹是什么呢?
对于圆,易得以下结论.
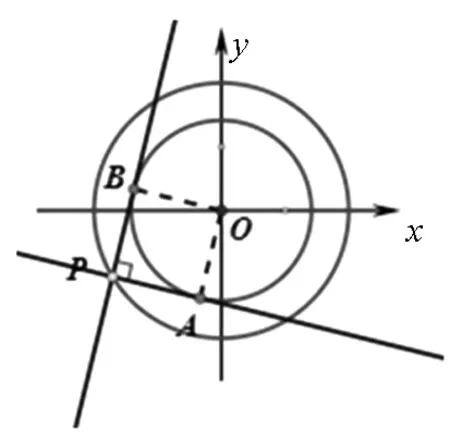
图2
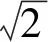
该结论证明较简单,略.
对于椭圆呢?可以遵循从特殊到一般,先猜想后证明的思路.
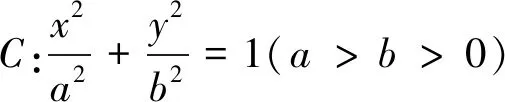
经网络画板(数学作图软件)模拟,结果正确.
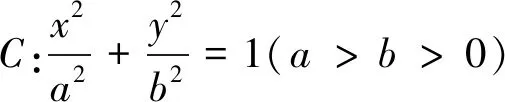
用证明定理1的方法,类似地也可以证明.为简化计算,这里采用参数坐标来证明.如图3.
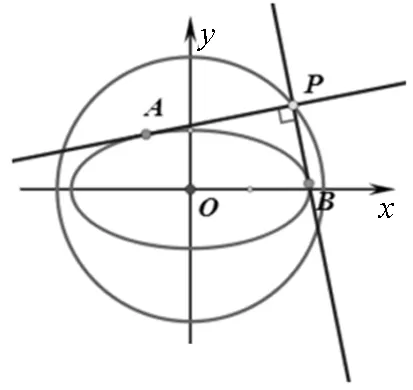
图3
(1)纯粹性.设
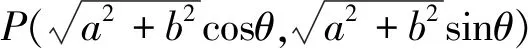
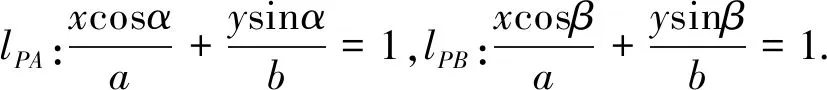
用类似的思路探究双曲线,又得到以下结论.
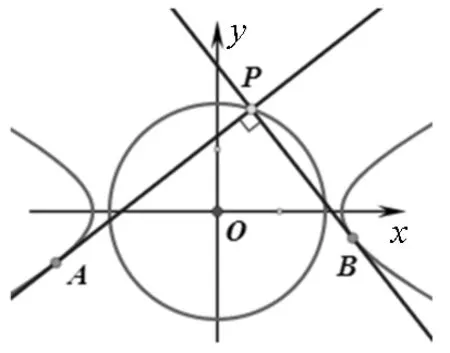
图4
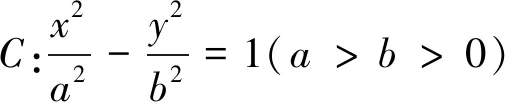
证明方法类似定理3,略.
以上后三个定理还可以统一为以下形式.
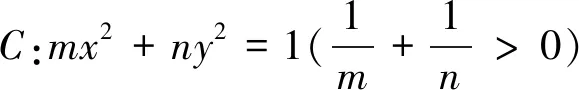
猜你喜欢
中学生数理化·中考版(2022年8期)2022-06-14
中学数学研究(江西)(2022年5期)2022-05-08
中学数学研究(江西)(2021年8期)2021-09-06
中学生数理化(高中版.高二数学)(2021年2期)2021-03-19
甘肃教育(2020年14期)2020-09-11
新世纪智能(数学备考)(2020年12期)2020-03-29
中学数学杂志(初中版)(2019年4期)2019-09-18
中学生数理化·中考版(2019年8期)2019-07-13
课程教育研究(2017年26期)2017-08-02
福建中学数学(2013年1期)2013-03-06

