机抖式激光陀螺抖动效率影响因素研究*
郭建刚,黄世涛,李志华,郑 伟
0 引 言
基于机抖式激光陀螺仪的激光捷联惯导系统,具有性能稳定、可靠性高、工作寿命长、动态范围广等一系列优点[1].我国绝大部分现役火箭,以及嫦娥探测器等,均采用了激光捷联惯导系统用以测量载体姿态和位置信息.随着航天技术的发展,控制系统对惯导系统可靠性和集成小型化的要求也越来越高.
机抖式激光陀螺仪(DRLG)采用机抖偏频技术消除陀螺闭锁误差[2-4],陀螺工作时抖轮以其谐振频率持续抖动.陀螺起抖时外部的反馈控制回路通过检测陀螺抖动幅值,并与理想值进行比较,如果检测到的抖动幅度值小于理想值,控制回路就增大电压,直到抖动幅度达到理想值.
工程应用中发现,DRLG集成安装到一个IMU上之后,其抖动效率常有显著降低,并导致陀螺精度的损失和导航精度的下降[5-6],部分情况下陀螺甚至不能正常起抖.因此,捷联惯导的系统设计对陀螺抖动效率也有着重要影响.而且,随着捷联惯导技术向小型化和多表冗余方向的探索,由于IMU的小型化以及仪表数量的增加,DRLG经系统集成后发生抖动效率降低和精度损失的情况更加严重.例如某武器型号惯导系统,为满足型号需求,其IMU进行了小型化设计,体积和重量显著降低.但样机阶段经试验发现,系统状态下陀螺抖动效率和精度均显著降低,抖动驱动接近饱和,而拆解后单陀螺性能良好.在既往的研究中,主要针对固定基座上单陀螺系统,通过改善抖动控制电路功能和效率、提高对陀螺抖频的跟踪精度等措施,提高陀螺抖动效率,如文献[7-9].姚建军等[10]基于单陀螺惯导系统模型,对陀螺抖动随IMU固有特性的变化规律进行了讨论,但力学模型中没有考虑抖轮抖动力矩对动基座的反作用.
综上,从系统设计角度开展陀螺抖动效率影响因素的研究,掌握对陀螺抖动效率影响显著的系统设计因素及其规律,将为捷联惯导系统的设计提供指导和依据,特别对捷联惯导系统的小型化和多表冗余设计有重要意义.
1 系统动力学模型
1.1 陀螺固定基座动力学模型
只考虑陀螺一阶模态,则机抖式激光陀螺在固定基座上的动力学模型可简化为如图1所示.
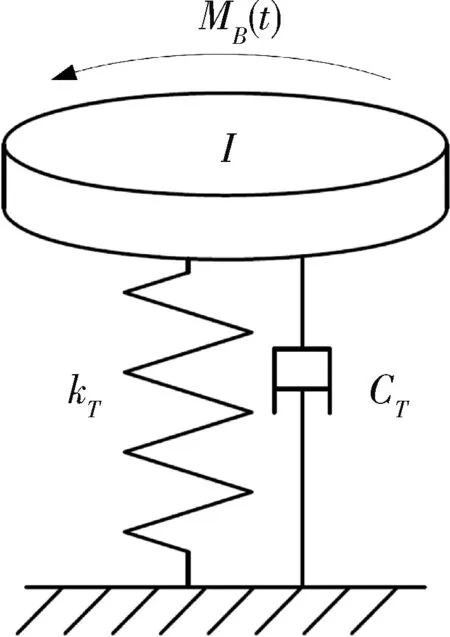
图1 陀螺抖动模型Fig.1 Model of the gyro dithering
其中MB(t)为基座产生的扭转力矩,且有MB(t)=Psin(ωt),I为陀螺腔体的转动惯量,则陀螺的激光谐振腔的运动微分方程如下:
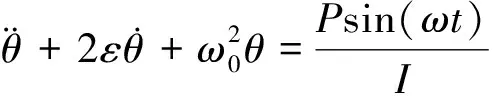
(1)
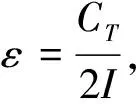
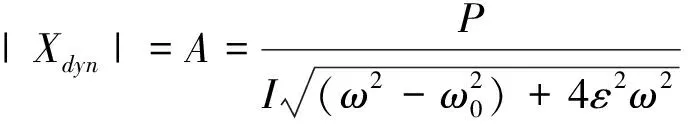
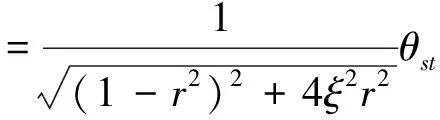
(2)
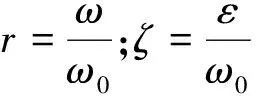
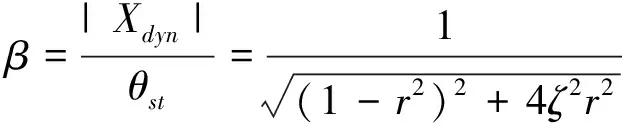
(3)
从式(2)和(3)中可以看出,对于固定基座上的单陀螺,抖动效率只与陀螺阻尼和驱动频率的跟踪精度有关.阻尼比ζ=0.006时,动力放大系数β与频率比r的关系如图2,其中βr=1=83.3.
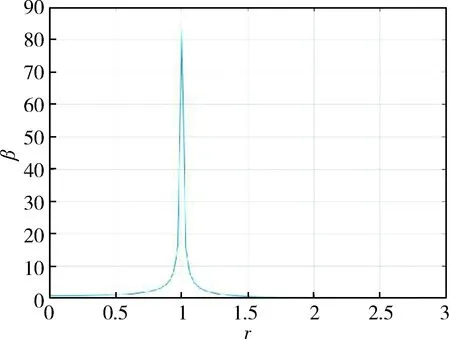
图2 动力放大系数β与频率比r关系图Fig.2 The relationship between dynamic amplificationfactor β and frequency ratio r
1.2 单陀螺IMU系统动力学模型
激光捷联惯导系统通常采用内减振设计,在IMU与惯组外壳体之间设计安装多个减振器,以有效隔绝外界力学环境对惯性仪表的影响,提高仪表测量精度和环境适应能力,此时陀螺通过抖轮安装在IMU上,IMU通过减振系统安装在惯导壳体上.因此IMU并不是固定不动的,对陀螺而言不再是固定基座问题.
考虑单个陀螺的情况并将壳体看作刚体,则简化为二自由度系统模型,如图3所示.
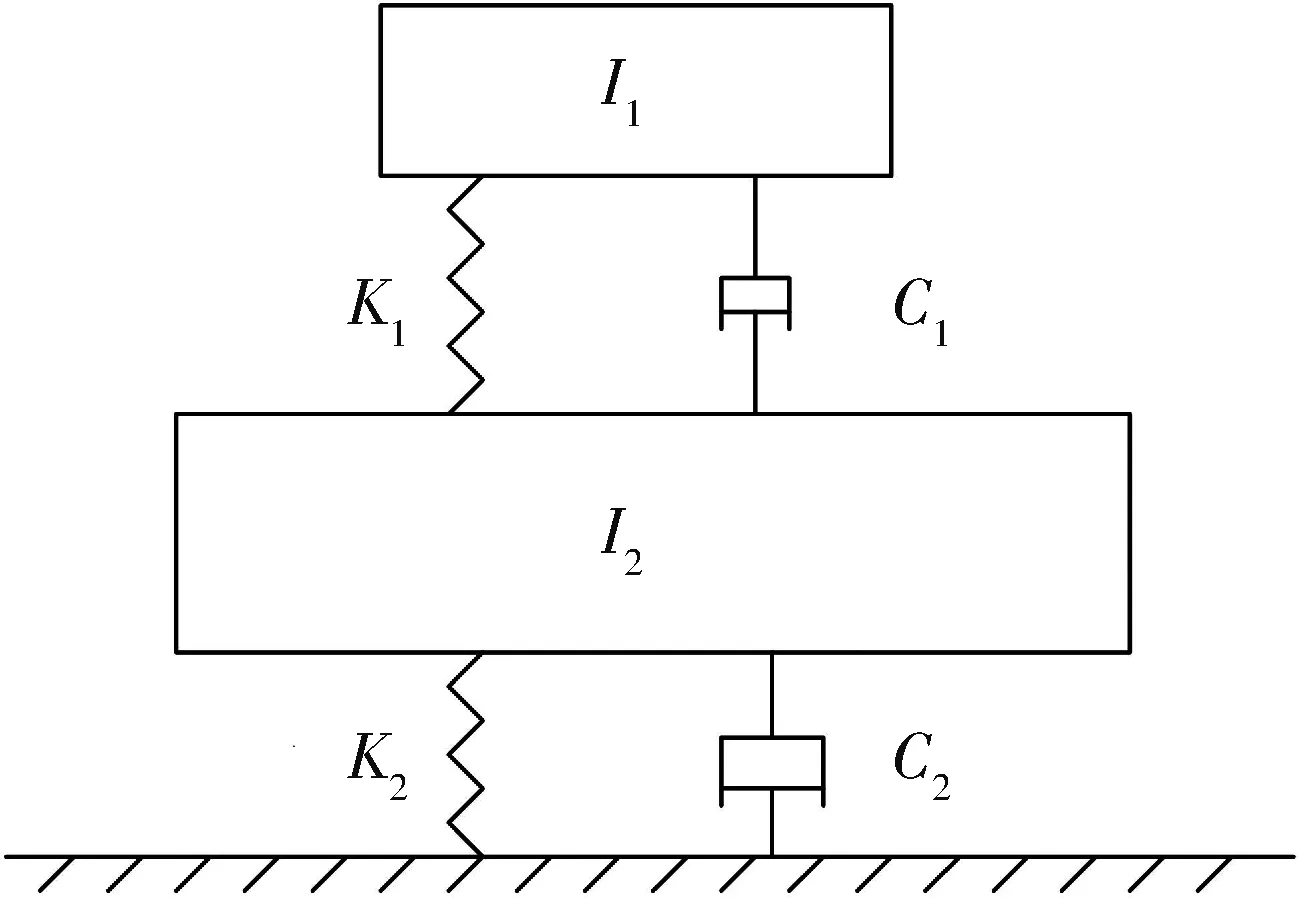
图3 系统动力学模型Fig.3 System dynamics model
其中,I1是陀螺转动惯量,K1是抖轮扭转刚度系数,C1是抖轮扭转阻尼系数;I2是IMU(除陀螺外)转动惯量,K1是抖轮扭转刚度系数,C2是减振系统的扭转阻尼系数.
当陀螺正常工作时,抖轮在压电陶瓷的作用下对陀螺玻璃腔体施加一个正弦变化的扭转力矩,同时对IMU施加一个反作用力矩.用θ1、θ2分别表示陀螺和IMU的绝对角位移,根据Lagrange方程,系统的动力学模型可表示为:
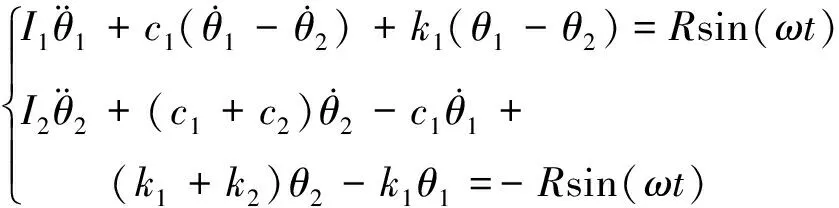
(5)
其中Rsin(ωt)为抖轮产生的扭转力矩,分别作用在陀螺腔体和IMU上,上式写成矩阵形式为:
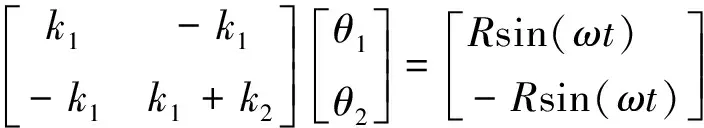
(6)
其无阻尼自由振动微分方程的特征方程为:
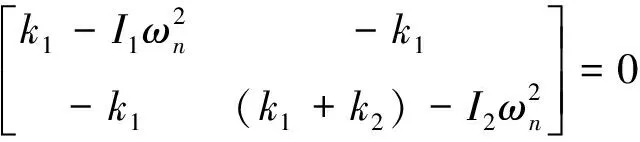
(7)
求解特征方程得到两个特征值,即为系统的两阶固有频率:
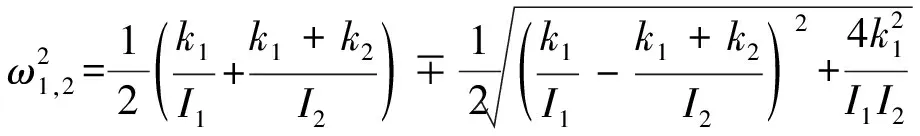
(8)
2 抖动效率影响因素分析
根据式(6)所示的系统动力学模型,决定陀螺抖动效率的因素包括:陀螺转动惯量,抖轮扭转刚度系数,抖轮扭转阻尼系数;IMU(除陀螺外)转动惯量,减振系统的扭转阻尼系数六个参数.为与惯导系统设计和测试过程中的常用参数相一致,将上述参数等效转换为:转动惯量比、陀螺抖频、减振系统扭转频率、抖轮阻尼系数和减振系统扭转阻尼系数,其中陀螺抖频选择和减振系统扭转频率设计也称为IMU频率分配设计,抖轮阻尼系数和减振系统扭转阻尼系数也统称为IMU阻尼特性.
对转动惯量比rx进行如下定义:IMU(不含陀螺)沿陀螺轴向的转动惯量与单陀螺抖动轴向的转动惯量之比,如式(9)所示.
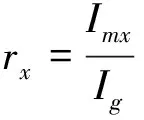
(9)
其中,Imx是IMU(不含X陀螺)沿X陀螺轴向的转动惯量;Af是X陀螺抖动轴向的转动惯量.
对陀螺抖动效率ex进行如下定义:同样驱动力矩下,陀螺安装在IMU上的抖动幅值与陀螺安装在固定基座上的抖动幅值之比,也即陀螺安装在IMU上的动力放大系数与陀螺安装在固定基座上的动力放大系数之比,理想值为1(100%),如式(10)所示.
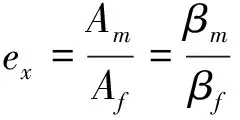
(10)
其中,Am和βm分别是X陀螺安装在IMU上的抖动幅值和动力放大系数;Af和βf分别是X陀螺安装在固定基座上的抖动幅值和动力放大系数.
根据如式(6)所示的系统动力学微分方程,基于Matlab软件,以抖频为350 Hz的某型激光陀螺和减振系统扭转频率约为110 Hz的某型号IMU的相关实际参数为参考,针对转动惯量比、IMU频率分配、系统阻尼等IMU设计因素对陀螺抖动效率的影响进行仿真分析.
2.1 转动惯量比和IMU频率分配对抖动效率的影响
由于机抖式激光陀螺仪的产品化非常成熟,激光惯导系统在设计时只需根据控制系统要求在陀螺仪产品型谱中进行选择,因此陀螺本身的转动惯量和抖频基本是固定的.影响转动惯量比和IMU频率分配的主要因素是IMU转动惯量和减振系统扭转频率.
仿真得到不同减振系统扭转频率下陀螺抖动效率随转动惯量比的变化曲线,如图4所示;不同减振系统扭转频率下IMU抖动幅值随转动惯量比的变化曲线,如图5所示;不同转动惯量比下陀螺抖动效率随减振系统扭转频率的变化曲线,如图6所示;不同转动惯量比下IMU抖动幅值随减振系统扭转频率的变化曲线,如图7所示.
从结果中可以看出,转动惯量比越大,陀螺抖动效率越高;陀螺抖频与减振系统同方向扭转模态频率差值越大,陀螺抖动效率越高;且当抖动惯量比较低,或者陀螺抖频与减振系统扭转模态频率差值较小时,两者的变化对陀螺抖动效率的影响更显著;同时陀螺抖动效率越高对应IMU抖幅就越低.
2.2 IMU阻尼特性对抖动效率的影响
仿真得到陀螺抖动效率随抖轮阻尼系数C1的变化曲线如图8所示,随减振系统阻尼系数C2的变化曲线如图9所示.
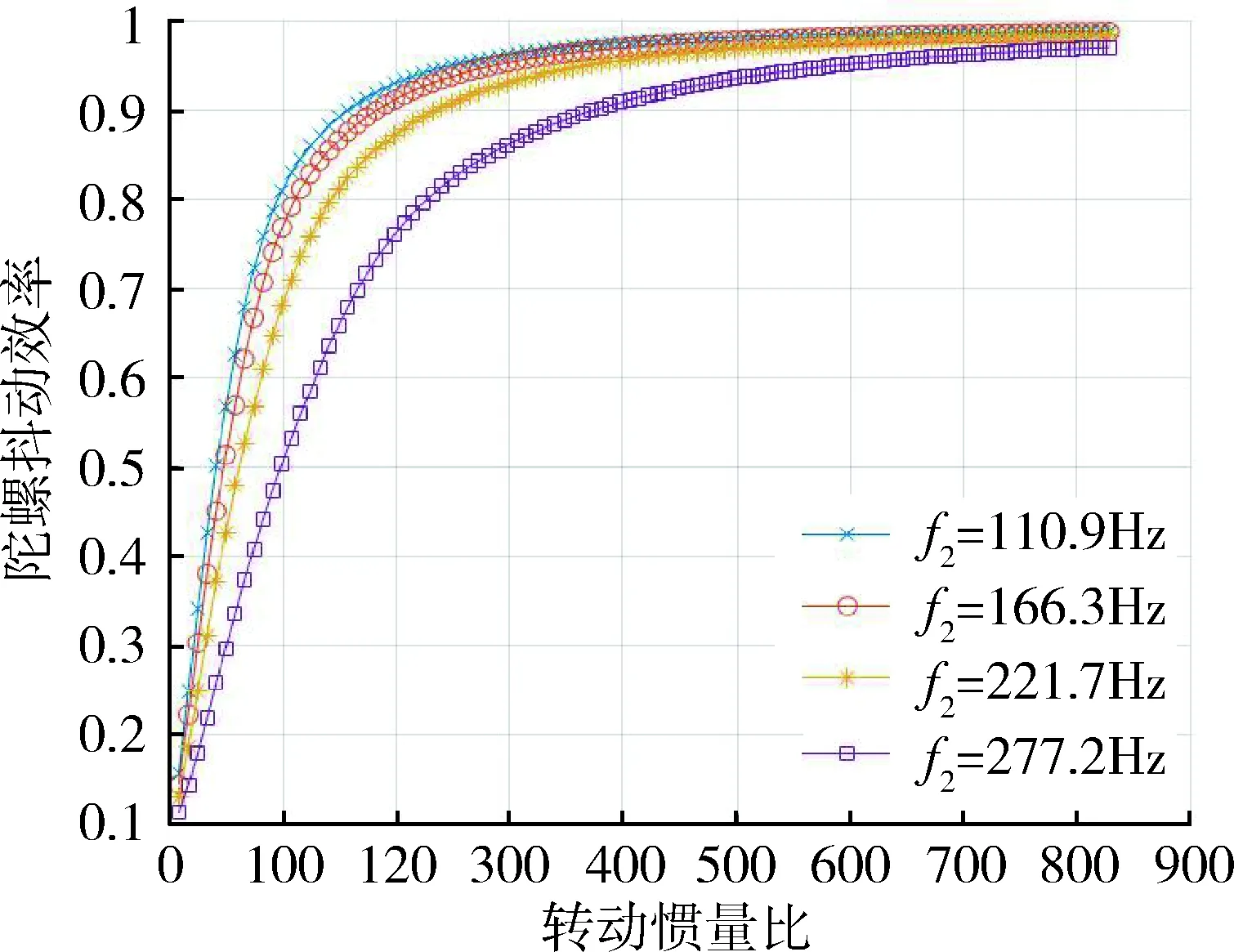
图4 陀螺抖动效率随转动惯量比变化曲线Fig.4 The dither efficiency with the ratio ofrotational inertia
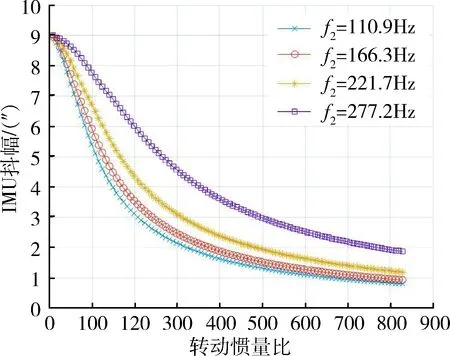
图5 IMU抖幅随转动惯量比变化曲线Fig.5 The IMU dither amplitude with the ratio ofrotational inertia
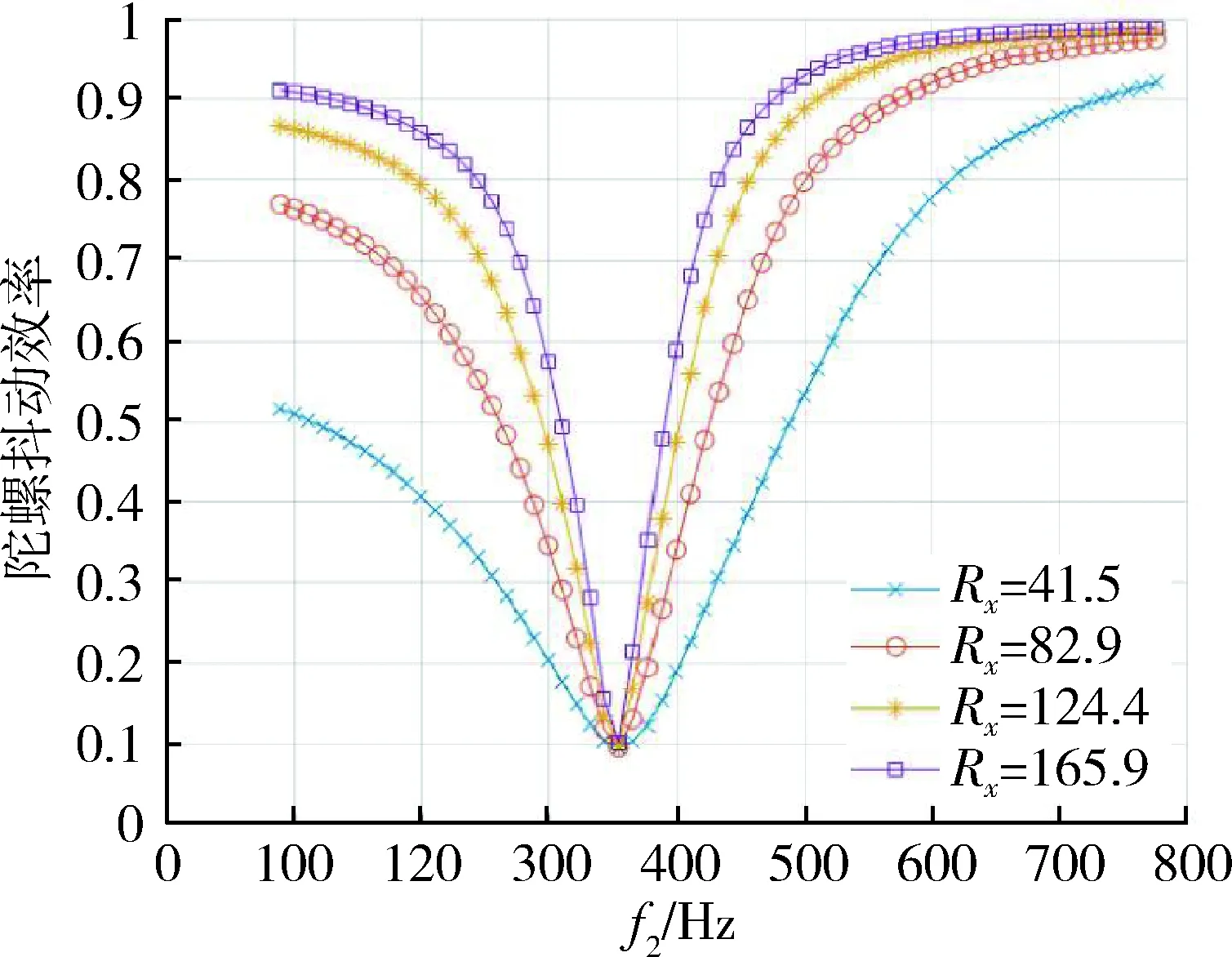
图6 陀螺抖动效率随减振系统一阶扭转频率变化曲线Fig.6 The dither efficiency with first order torsionalfrequency of damping system
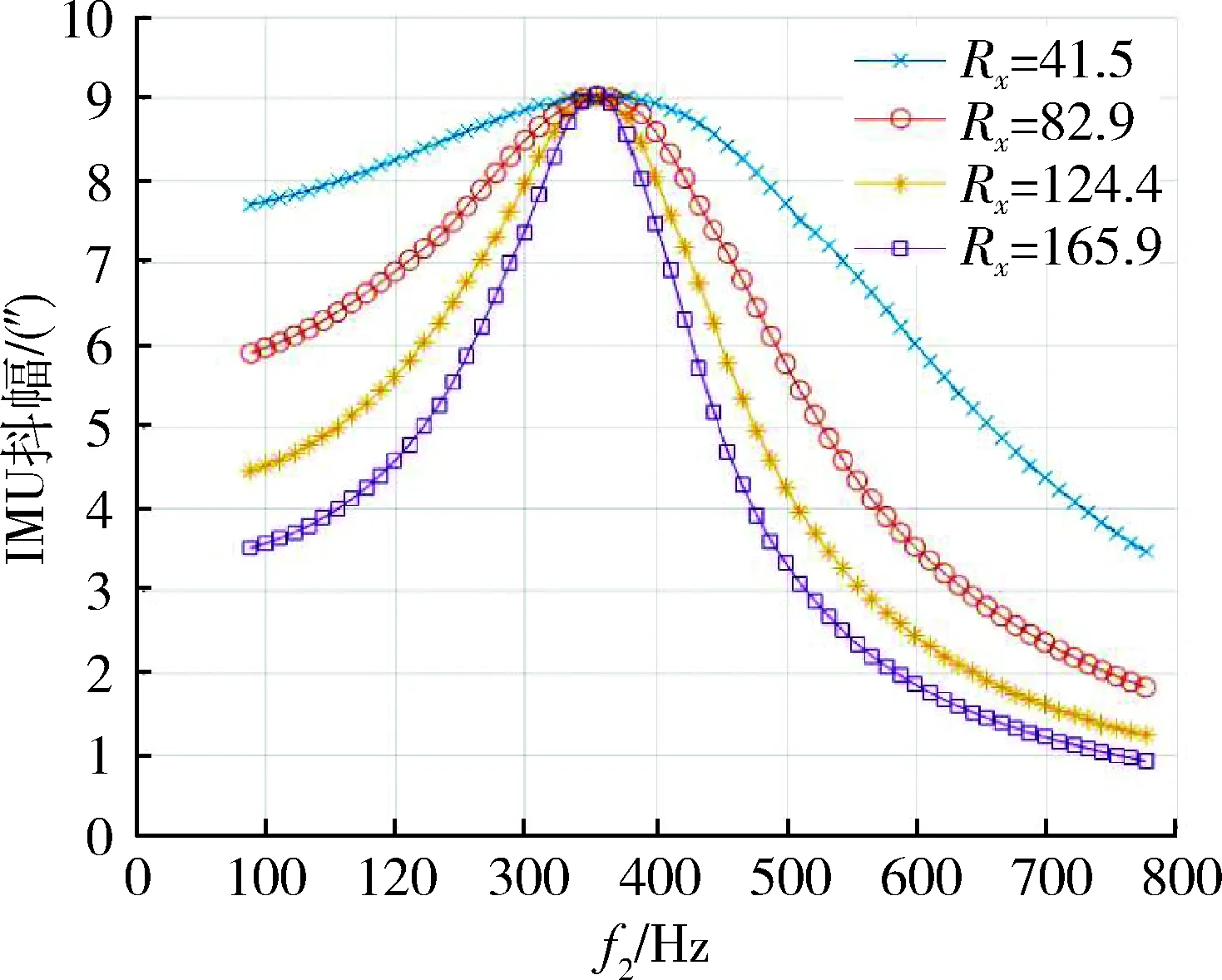
图7 IMU抖幅随减振系统一阶扭转频率变化曲线Fig.7 The IMU dither amplitude with first ordertorsional frequency of damping system
图8 陀螺抖动效率随抖轮阻尼系数的变化曲线Fig.8 The dither efficiency with dampingcoefficient of gyro
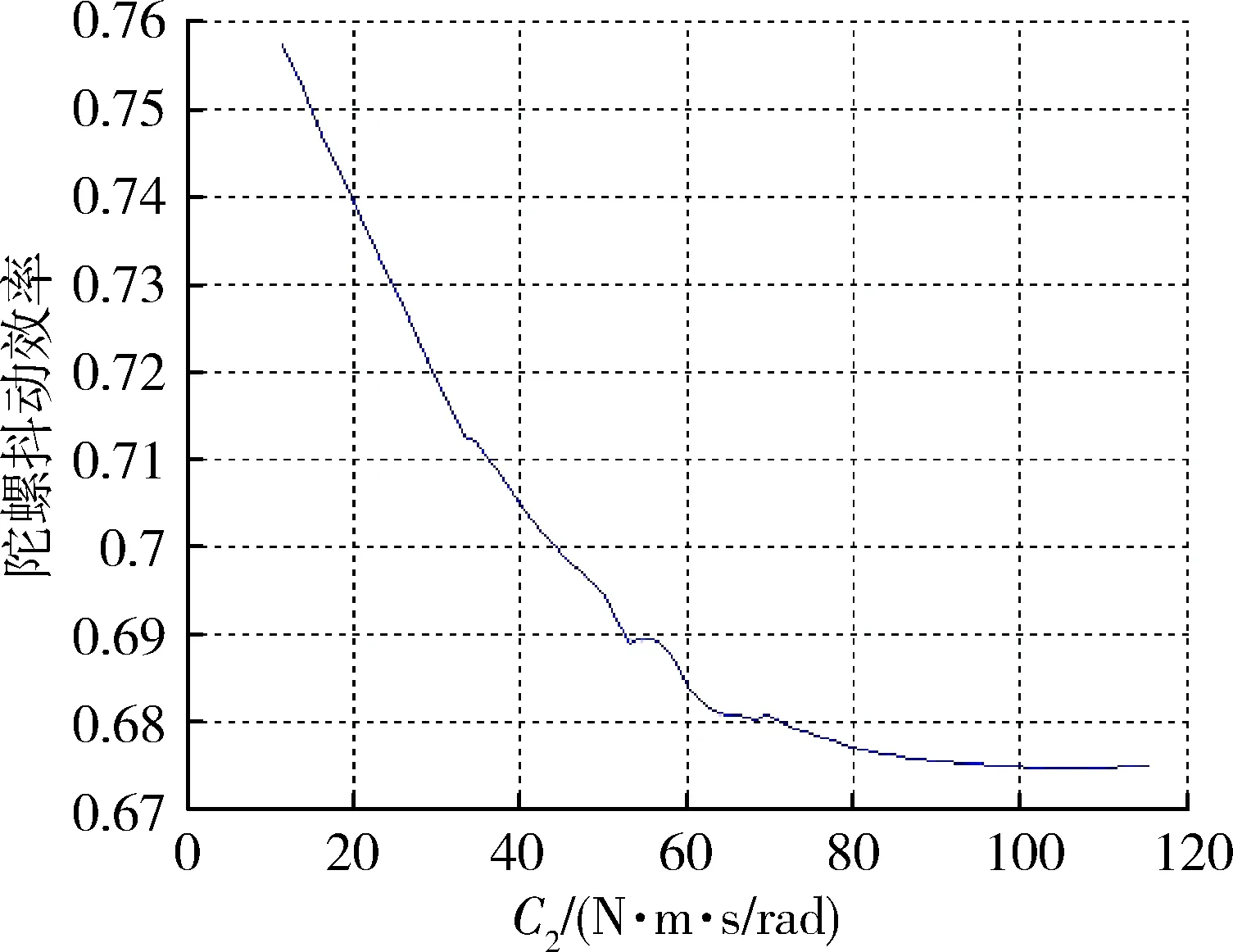
图9 陀螺抖动效率随减振系统扭转阻尼系数的变化曲线Fig.9 The dither efficiency with damping coefficientof damping system
从结果中可以看出,陀螺抖动效率均随着抖轮阻尼系数和减振系统阻尼系数的提高而降低;同时陀螺抖动效率对抖轮阻尼系数的提高变化更加显著,因此陀螺抖动效率对抖轮阻尼系数更加敏感,也与抖轮阻尼系数显著低于减振系统的阻尼系数有关.
3 系统设计方法和原则
根据上述分析结果,陀螺抖动效率代表了抖轮抖动能量在陀螺腔体和IMU之间分配情况.抖动效率越高,代表陀螺腔体的能量占比越高,IMU的抖动振动越小.抖动效率的降低不仅意味着抖动偏频有效性的降低,直接影响陀螺精度;同时也代表陀螺抖轮传递到IMU上的抖动能量增加,导致陀螺之间抖动耦合误差的增大,进一步降低了陀螺精度.因此,提高陀螺抖动效率是DRLG捷联惯导解耦设计,保障系统集成后陀螺精度的基础.
3.1 提高抖动效率的系统设计方法和原则
对提高陀螺抖动效率的系统设计方法和原则进行总结,如下.
(1) 提高IMU抖动惯量比
在惯导系统重量指标一定的情况下,可以通过优化IMU零部件装配和质量分布,以及增加IMU集成安装的零部件数量等方式,有效提高IMU转动惯量.
(2) 提高陀螺的抖动频率与减振系统同方向扭转模态频率的差值
减振系统扭转模态与减振器刚度、数量和分布均有关系,当减振器刚度和数量受到减振系统线振动模态频率限制时,可以通过调整减振器分布特别是调整减振器与减振系统弹性中心的距离,对某一轴向的扭转模态频率进行有效调整.
(3) 降低陀螺抖轮阻尼系数
单陀螺仪设计应该力求降低抖轮的阻尼系数,可以通过优化抖轮设计,减少过渡零件数量,减少胶粘工艺等措施实现.
通过对各型陀螺和减振器的相关参数的进行测试和统计,利用本文的方法可以在捷联惯导系统设计阶段对陀螺抖动效率进行较为准确的预估.
3.2 工程应用和验证
在某型基于90型DRLG的高精度小型化捷联惯导的设计中,根据上述设计方法和原则,采取了一系列的设计措施,主要如下.
(1) 由于所选用90型DRLG的抖动惯量一定,因此在设计中只能通过提高IMU转动惯量来提高转动惯量比.在对热、力等条件进行充分核算之后,将部分功能电路等组件集成安装到了IMU上,以提高IMU的转动惯量,同时有助于提高整机集成度和小型化.
(2) IMU结构设计中,对各组件装配和质量分布进行了优化,增加高密度组件与IMU质心的距离.通过将密度较大的铝合金基体和陀螺表头等排布在IMU外围,进一步提高了IMU的抖动惯量.
(3) 由于减振方式和IMU质量分布等原因,减振系统在三个轴向的扭转模态频率并不一致.在模态仿真和试验测试的基础上,对各轴向陀螺的抖频进行匹配,避免某个轴向陀螺抖频和减振系统扭转模态频率过于接近.
最终该型惯导系统,总重约9.6 kg,其中IMU约5.6 kg.测试结果,陀螺精度优于6‰°/h,与单陀螺固定基座状态相当,陀螺抖动驱动在理想范围内;1 000 s静态导航试验,位置误差42 m,精度良好.而同等精度的其它激光捷联惯导系统的重量一般在15~20 kg左右,该型惯导系统实现了显著的小型化,如图10所示.
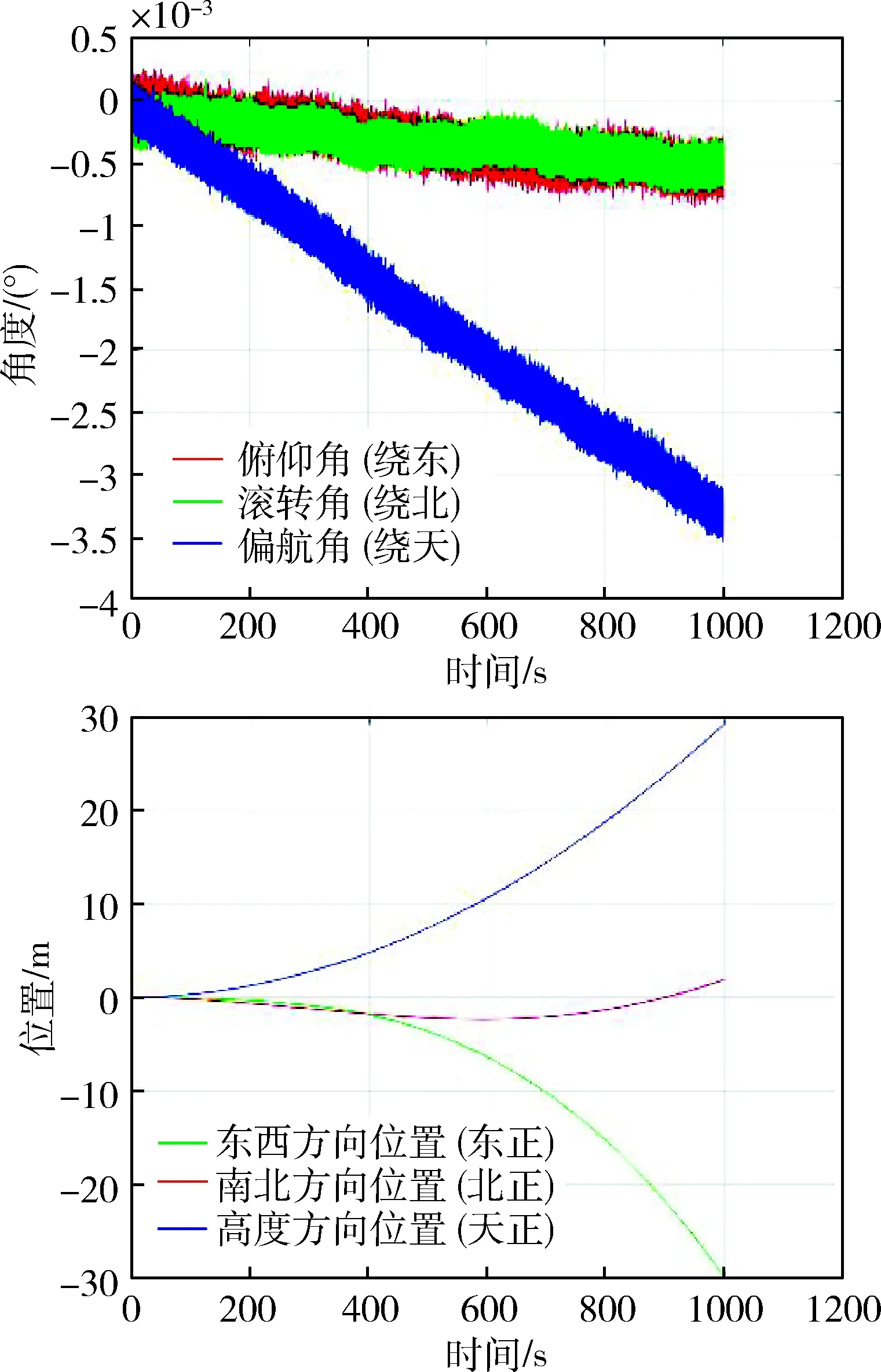
图10 静态导航试验结果Fig.10 Static navigation experiment results
4 结 论
陀螺抖动效率实际代表了抖轮的抖动能量在陀螺腔体和IMU之间分配情况,提高陀螺抖动效率,有助于抑制陀螺间的相互影响,是陀螺解耦设计的关键.IMU抖动惯量比、陀螺抖动频率与减振系统扭转模态频率的差值以及系统阻尼均对陀螺抖动效率有显著影响.IMU抖动惯量比越高、陀螺抖动频率与减振系统在同方向上扭转模态频率的差值越大、陀螺抖动机构的阻尼系数越低,则惯导系统集成后陀螺抖动效率越高.工程应用验证表明,将更多的组件集成安装到IMU上,是提高陀螺抖动效率,保障陀螺精度,实现惯导系统小型化的有效途径.惯导系统小型化设计的最理想状态应是所有仪表和电路组件等均集成安装在IMU上,即除机箱外壳外只有一个IMU.

