基于等价可靠性模型的姿态敏感器配置优化及分析*

冯佳佳，王佐伟，崔 振

0 引 言

航天器姿态敏感器主要包含地球敏感器、太阳敏感器、星敏感器、陀螺等器件，它们向航天器提供航天器所需的姿态信息等.航天器姿态敏感器配置主要指的是姿态敏感器类型的选择、安装、指向等.由于姿态敏感器的配置直接影响到航天器任务的完成程度，因此，航天器姿态敏感器的配置情况对航天器控制系统设计来说至关重要[1].

目前，在工程中，航天器控制系统中的姿态敏感器主要采取经验及继承进行配置，缺少相应的理论支撑.虽然目前还没有公开的文献对航天器整个姿态敏感器的配置情况进行过研究，不过在器件配置方法上取得了一定的研究成果.文献[2-5]以故障可诊断性为基础对器件的配置方法进行过研究；文献[6-10]以多目标优化为基础对器件的配置方法进行过研究；文献[11-13]以可靠性为目标对器件的配置方法进行过研究；文献[14-16]以综合评价为基础对器件的配置方法进行过研究.然而，在进行航天器姿态敏感器配置时，由于需要综合考虑器件的冗余备份和功能实现备份两者之间的关系，以及器件的工作任务阶段、工作时长、姿态确定精度等问题，因此姿态敏感器配置问题会显得格外复杂.一般来说，姿态敏感器器件类型的选择和器件冗余备份的个数会直接影响到系统的可靠性以及每个任务阶段可选方案的数目及类型等，而每个可选方案在姿态确定精度、实现方式等方面均具有优劣.因此，如何确定姿态敏感器器件的类型及冗余备份的个数是航天器姿态敏感器配置首先需要解决的问题.

本文针对航天器控制系统设计中如何进行姿态敏感器配置这一问题，提出了一种确定最优姿态敏感器配置的方法.首先，从航天器控制系统设计中提炼出姿态敏感器配置的数学问题；然后，针对该问题建立一套以任务可靠性为基础的等价模型，在该可靠性模型中将航天器任务阶段可选方案之间性能的优劣以等价因子的形式等价到系统可靠性模型中，而不丢失任何性能指标；最后，根据等价可靠性的计算数值确定出最优的姿态敏感器配置方案.

1 问题描述

设某一航天器需要进行姿态敏感器配置，现有的可选姿态敏感器类型为S1,S2,S3,…，Sn.设对航天器工作任务分析可知，航天器共经历P个任务阶段，由于航天器在每个阶段所执行的任务不一样，因此所采用的姿态敏感器组合可能不一样.

设航天器在第i个任务阶段中，满足姿态确定精度的可选姿态敏感器组合方案为：

Ωi={ni1,1×Si1,1+ni1,2×Si1,2+…+ni1,M×Si1,M;

orni2,1×Si2,1+ni2,2×Si2,2+…+ni2,N×Si2,N;

⋮

ornis,1×Sis,1+nis,2×Sis,2+…+nis,Q×Sis,Q}

(1)

其中，ni1,1,ni1,2,ni1,M,ni2,1,ni2,2,ni2,N,…,nis,1,nis,2,nis,Q为姿态敏感器的个数；Si1,1,Si1,2,Si1,M,Si2,1,Si2,2,Si2,N,…,Sis,1,Sis,2,Sis,Q为姿态敏感器的类型，它们之间可能会有重叠.

经过对航天器整个任务阶段的分析，设最终确定的航天器姿态敏感器配置方案为：

Ω={NI×SI+NJ×SJ+…+NV×SV}

(2)

由于航天器姿态敏感器的配置会直接影响到系统任务的可靠性，姿态敏感器可选组合方案的类型及姿态确定精度，因此，如何确定姿态敏感器个数NI,Nj,…,NV和姿态敏感器类型SI,Sj,…,SV，使姿态敏感器的配置方案为最优，这是本文研究的主要内容.

2 姿态敏感器配置的确定

2.1 等价可靠性模型

在进行姿态敏感器配置时，首先需要考虑的问题是系统的可靠性.

由于对于确定的姿态敏感器配置方案来说，它在航天器每个任务阶段中的可选组合方案数目及类型是确定的，因此，对于一个确定的姿态敏感器配置来说，系统的可靠性模型可以表示成如图1所示的形式，其中，Rij表示为航天器第i个任务阶段的第j个可选组合方案的可靠性.

图1 系统可靠性模型Fig.1 System Reliability Model

(3)

则，整个系统的可靠性为：

R=[1-(1-R11)(1-R12)…(1-R1u)]·

[1-(1-R21)(1-R22)…(1-R2v)]·

…[1-(1-Rp1)(1-Rp2)…(1-Rpz)]

(4)

由于在任务的每个阶段，所有可选的组合方案在姿态确定精度、实现方式等方面均有优劣，因此，为了更加准确的在系统中反应出可选组合方案的优劣，特别的引入等价因子这一概念.

引入等价因子后，系统的可靠性模型表示成如图2所示.

图2 系统等价可靠性模型Fig.2 System Equivalent Reliability Model

图2中，αij表示为航天器第i个任务阶段的第j个可选方案的等价因子，它表示为将可选组合方案在姿态确定精度、实现方式等方面的差异以可靠性的形式等价表示出来，它反映了该可选组合方案的综合指标问题，一般情况下，αij∈(0, 1]

则，引入等价因子后，整个系统的等价可靠性可以表示为：

R=[1-(1-α11R11)(1-α12R12)…(1-α1uR1u)]·

[1-(1-α21R21)(1-α22R22)…(1-α2vR2v)]·

…[1-(1-αp1Rp1)(1-αp2Rp2)…(1-αpzRpz)]

(5)

系统可靠性模型引入等价因子后，整个系统的可靠性可以表示为在考虑系统综合指标的前提下航天器姿态敏感器配置的优劣情况，该数值综合反映了敏感器配置的可靠性、姿态确定精度、实现方式等综合指标问题.

下面需要对等价因子进行确定.

2.2 等价因子的确定

为了使等价因子能够综合表示出系统的综合指标问题，并且表示的科学合理，可以将其定义为：在航天器的某一任务阶段，可选组合方案相对于可选组合方案中的最优方案在除可靠性以外的综合指标上的等价程度等价于系统可靠性的程度.它包含两个指标，一个指标为可选组合方案相对于可选组合方案中的最优方案在除可靠性以外的综合指标上的等价程度，第二个指标为除可靠性以外的综合指标相对于系统可靠性的等价程度.

因此，αij可以表示为：

αij=β0ηij

(6)

其中，β0为系统设计时除可靠性以外的综合指标相对于可靠性的等价程度，定义为：

(7)

其中，ωrel为系统设计时可靠性这一指标所占的权重，ωother为系统设计时除可靠性以外的其他综合指标所占的权重，其具体权重可以由层次分析法[17]进行计算得到，也可以由设计师在考虑总体方案时给定.由于在系统设计时，所有姿态敏感器的可选组合方案都满足姿态确定精度这一指标，并且都以可靠性为首要设计指标，因此，在系统设计时，一般情况下，β0∈(0, 1].

ηij为姿态敏感器可选组合方案相对可选组合方案中的最优方案在除可靠性以外的综合指标中的等价程度，一般可由综合评价方法计算得到.

下面给出ηij的具体计算方法：

为了对姿态敏感器可选组合方案进行综合评价和分析，需要建立规范、合理的指标评价体系.通过对系统设计时姿态敏感器配置指标的分析可知，姿态敏感器配置时考虑的除可靠性以外的综合指标含义及计算方法如下所示：

(1) 质量(M)，本文主要指姿态敏感器可选组合方案中各器件质量的加和值.

(2) 成本(C)，本文主要指姿态敏感器可选组合方案中各器件总研制成本.

(3) 方案能耗(E)，本文主要指姿态敏感器可选组合方案中各器件额定功率总和.

(4) 姿态确定精度、实现方式等其他因素(O)，本文主要是指姿态敏感器可选组合方案在算法实现上的姿态确定精度、复杂程度、计算机资源利用情况等.由于每个任务阶段在实现程度、精度要求上都不一致，该指标很难进行具体数值计算.因此，该部分将利用有经验的设计人员进行打分的形式来表示该指标[18].

(8)

其表示为在第i个任务运行阶段中，方案集Ki对评价指标集Φ的评价指标矩阵.

设由层次分析法计算得到的各指标权重为W=[ω1ω2ω3ω4]，则航天器第i个运行任务阶段的第j个可选方案的评价值为：

(9)

设第i个运行任务阶段中，可选组合方案中最优方案的评价值为yi0，则：

(10)

由于ηij是姿态敏感器可选组合方案相对于可选组合方案中最优方案的等价程度，因此，一般情况下，ηij∈(0, 1].

综合以上分析可知，可以根据式(6)～(10)确定出等价因子，最终可以通过对比等价可靠性模型的计算数值确定出最优的姿态敏感器配置方案.

3 实例解析

3.1 姿态敏感器配置方案分析

设某一高轨卫星需要进行姿态敏感器配置，根据目前的实际情况分析共有三种配置方案，分别为：{2×太阳敏感器+1×地球敏感器+2×星敏感器+6×陀螺}；{2×太阳敏感器+3×星敏感器+4×陀螺}；{4×太阳敏感器+2×地球敏感器+9×陀螺}.根据对高轨卫星任务阶段分析，假设在满足姿态确定精度的前提下，在每个运行任务阶段所使用的姿态敏感器组合及最少工作数量情况如表1所示，其中：P1表示为太阳捕获阶段，P2表示为地球捕获指向阶段，P3表示为远地点点火阶段，P4表示为位置保持阶段，P5表示为正常工作阶段.

表1 姿态敏感器组合及最少工作数量情况Tab.1 Attitude Sensor Combination and Minimum Work Number

续表

任务阶段方案1方案2方案3P3Ω31:1×星敏+3×陀螺;Ω32:2×太敏+3×陀螺;Ω33:3×陀螺Ω31:1×星敏+3×陀螺;Ω32:2×太敏+3×陀螺;Ω33:3×陀螺Ω31:2×太敏+3×陀螺;Ω32:3×陀螺P4Ω41:2×星敏+3×陀螺;Ω42:2×星敏;Ω43:1×地敏+2×太敏+3×陀螺;Ω44:3×陀螺Ω41:2×星敏+3×陀螺;Ω42:2×星敏;Ω43:3×陀螺Ω41:1×地敏+2×太敏+3×陀螺;Ω42:3×陀螺P5Ω51:2×星敏+3×陀螺;Ω52:2×星敏;Ω53:1×地敏+2×太敏+3×陀螺;Ω51:2×星敏+3×陀螺;Ω52:2×星敏;Ω51:1×地敏+2×太敏+3×陀螺

3.2 等价可靠性模型分析

在15年寿命要求下，地球敏感器的可靠性取值为0.984 1，太阳敏感器的可靠性取值为0.973 6，陀螺的可靠性取值为0.963 1，星敏感器的可靠性取值为0.982 7，则由式(3)可以计算得到：

方案1：R11=0.947 9，R12=0.999 7，R21=0.999 7，R22=1.000 0，R23=0.983 4，R31=0.999 7，R32=0.947 9，R33=1.000 0，R41=0.965 7，R42=0.965 7，R43=0.932 8，R44=1.000 0，R51=0.965 7，R52=0.965 7，R53=0.932 8；

方案2：R11=0.947 7，R12=1.000 0，R21=0.999 8，R22=0.999 8，R31=0.999 8，R32=0.947 7，R33=0.999 8，R41=0.998 9，R42=0.999 1，R43=0.999 8，R51=0.998 9，R52=0.999 1；

方案3：R11=0.999 9，R21=1.000 0，R22=0.999 6，R31=0.999 9，R32=1.000 0，R41=0.999 6，R42=1.000 0，R51=0.999 6.

下面开始计算等价因子，在这里设β0=1:

为了评价的公平性，在这里将三种配置方案在每一任务运行阶段的可选组合方案统一进行评价.根据各方案敏感器的配置情况，由式(8)建立的评价指标矩阵为：

P1阶段：方案1中Ω11、Ω12，方案2中Ω11、Ω12，方案3中Ω11组成的评价指标矩阵为(按顺序排列)：

P2阶段：方案1中Ω21、Ω22、Ω23，方案2中Ω21、Ω22，方案3中Ω21、Ω22组成的评价指标矩阵为(按顺序排列)：

Z2=

P3阶段：方案1中Ω31、Ω32、Ω33，方案2中Ω31、Ω32、Ω33，方案3中Ω31、Ω32组成的评价指标矩阵为(按顺序排列)：

P4阶段：方案1中Ω41、Ω42、Ω43、Ω44，方案2中Ω41、Ω42、Ω43，方案3中Ω41、Ω42组成的评价指标矩阵为(按顺序排列)：

P5阶段：方案1中Ω51、Ω52、Ω53，方案2中Ω51、Ω52，方案3中Ω51组成的评价指标矩阵为(按顺序排列)：

经由层次分析法计算得到的评价指标权重为[17]：

W=[0.201 0;0.181 5;0.236 0;0.381 5]

将每一任务阶段中的评价指标矩阵进行规范化处理后，计算得到：

方案1：

α11=0.867 5，α12=0.783 0，α21=0.648 1，α22=0.839 6，α23=1.000 0，α31=0.636 7，α32=0.842 4，α33=0.687 4，α41=0.803 0，α42=0.990 2，α43=0.794 4，α44=0.687 2，α51=0.721 4，α52=1.000 0，α53=0.761 5；方案2：

α11=1.000 0，α12=0.736 4，α21=0.774 0，α22=0.971 5，α31=0.842 2，α32=1.000 0，α33=0.845 0，α41=1.000 0，α42=0.817 9，α43=0.872 3，α51=0.866 0，α52=0.845 1；

方案3：

α11=0.720 7，α21=0.591 8，α22=0.658 6，α31=0.577 9，α32=0.560 9，α41=0.716 0，α42=0.685 6，α51=0.691 2.

配置方案等价可靠性模型的具体关键数值如表2所示.

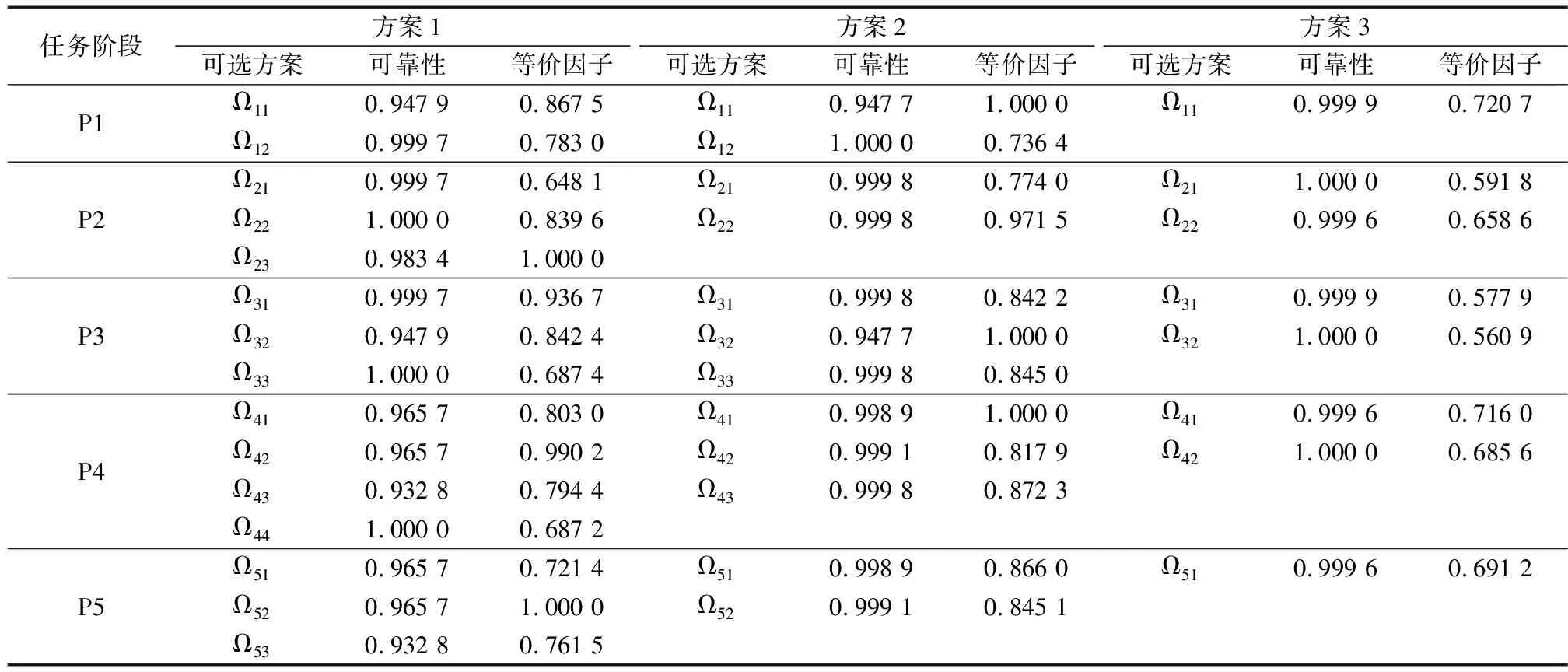
表2 等价可靠性模型关键数值Tab.2 Key values of equivalent reliability model

则，计算出各配置方案的等价可靠性分别为：

方案1：R=0.946 4

方案2：R=0.958 0

方案3：R=0.317 6

由姿态敏感器等价可靠性模型的计算数值结果可以确定出，配置方案2为最优的航天器姿态敏感器配置，经对其进行分析，该结论符合工程实际的配置情况.事实上，随着星敏感器技术的成熟及成本的下降，目前国际上敏感器配置的趋势是增加星敏感器的使用，并不断的减少及停止使用地球敏感器和太阳敏感器，这是符合技术发展的趋势.

需要说明的是：①本文在任务阶段中姿态敏感器组合的选取情况是依据某卫星平台设计阶段所考量的，可能与姿态敏感器组合的实际应用能力有出入；②在计算姿态确定精度、实现方式等指标时是采用的打分法，特别的引入了主观因素；③在每个任务阶段中，没有单独考虑任务运行阶段、姿态敏感器工作时长等问题，而是将其进行统一处理.因此，本文的研究均是在一定的前提下进行的，其对工程具有理论指导意义.

4 结 论

本文提出了一种确定航天器姿态敏感器最优配置的方法，该方法综合考虑了系统的可靠性、姿态确定精度、实现方式等综合指标问题，并利用该方法对一工程实例进行姿态敏感器配置的确定，结果表明该方法可行和有效，对工程具有理论指导意义.然而，在进行姿态敏感器配置时，本文没有考虑到航天器任务阶段的特殊性以及姿态敏感器工作时长等问题，这都将作为下一步研究的重点及方向.