空间碎片消旋柔性冲击末端设计与分析*

马 睿，戴士杰，张慧博，张德轩，姚金铭

0 引 言

为了满足通信、气象监测以及国际空间站维护等需求，人类每年都会进行大量的太空发射任务[1].空间碎片包括完成任务的火箭箭体和卫星本体、火箭的喷射物、空间物体之间的碰撞产生的碎块等.受到空间摄动力或力矩以及失效前自身残余角动量等因素的影响，空间碎片往往处于高速复杂翻滚运动状态，其数量的增长严重威胁了太空环境的安全稳定[2].对空间碎片消旋实际是指利用外部控制力矩衰减目标角速度的过程.接触式主动消旋方法可以提供较大的控制力，包括法向接触力和切向摩擦力，可达N数量级[3]，但仍然存在冲击力大小难以控制的问题.因此研究执行器末端与空间碎片之间的碰撞力可以为主动消旋控制方法的研究提供指导，保证空间环境的可持续利用.

消旋实现方式按作用力是否与目标接触主要分为接触式和非接触式两种.针对接触式消旋方法，国内外都已经开展了研究.JAXA的NISHIDA和KAWAMOTO等[4]提出利用减速刷与目标间的弹性接触力在抓捕前对目标进行消旋的方法.东京工业大学的 MATUNAGA等[5]将恒压弹性小球作为机械臂末端执行器，利用机械臂末端与目标表面之间弹性碰撞所产生的推力与摩擦力衰减目标转动.日本国家航空航天实验室的 KAWAMOTO等[3]利用多次接触脉冲作用力交替衰减目标章动角和自旋转速.HOVELL[6]利用粘弹性绳系附着到旋转空间碎片表面上，通过系绳拉力及变形时的阻尼力控制目标转速直至其姿态稳定的方法.现有的几种接触式消旋方法中，减速刷消旋冲击小，但效率较低；绳系机器人消旋在如何避免抓捕失败同时防止绳系缠绕还需要进一步研究.机械脉冲消旋制动效率最高，但碰撞风险很大，所以在进行消旋处理时要注意作用力的大小.

本文为了更准确地研究冲击末端与空间碎片的碰撞力，设计了变压力柔性末端，建立了非线性动力学模型，开展了单自由度碰撞实验，并将实验仿真结果与模型计算结果进行了对比分析.以期为空间碎片主动消旋捕获方法的发展供理论依据和必要的参考.

1 柔性末端设计

充气结构质量轻，成本低，外形易加工，现广泛应用于航空航天领域[7-9].很多学者对其力学压缩性能进行了研究.许月杰等[10-11]考虑了充气柱结构中的刚柔耦合作用，对充气柱机构压缩过程中的刚度和能量问题进行了研究.针对机械脉冲主动消旋，采用变压力柔性末端可以提供更大摩擦力，而且较刚性接触，对合作目标的保护性更好.

1.1 柔性末端结构参数确定

Matunaga等[5]建立的基于恒定压力弹性球的冲击模型，为完全弹性碰撞模型.事实上，在冲击过程中，随着变形量的增加，弹性球体积减小，压力增大，材料刚度等参数发生了非线性改变，进一步影响碰撞力大小.弹性阻尼器作为柔性末端的核心创新点，针对外太空温度极端、微重力、强辐射及强电磁等复杂环境，球膜材料选择乙丙橡胶，密度低，可填充，具有良好的耐天候，耐臭氧，耐热性能.柔性末端通过法兰固定于空间机械臂，通过控制机械臂实现消旋冲击.根据机械臂法兰的安装尺寸，确定外径为30 mm，结构如图1所示.

图1 充气球模型示意Fig.1 Inflatable ball model

考虑球膜与气门之间的气密性：

F/(πdh)≤σ

(1)

其中：F为碰撞力，d为气门直径，h为球膜厚度，σ为橡胶粘金属胶水的抗拉强度.计算得h≥8.3 mm时满足设计需求.

1.2 内部压力阈值确定

变压力柔性末端实物如图2所示，通过向球体内部充气改变内部压力值，压力传感器实时采集数值信号，进行反馈.

图2 弹性阻尼器Fig.2 Elastic damper

弹性阻尼器几何模型的参数见表1.机构具有对称性，为了节约计算资源，只建立1/2充气球体有限元型.

表1 阻尼器几何模型参数Tab.1 Geometric model parameters

采用四边形壳单元shell 181对几何模型进行网格划分，生成有限元模型如图3所示.本文分析对象主要在充气结构，分析它的不同内压作用下的刚度以及碰撞过程中的接触应力等，所以对其网格划分稠密一些，压板区域的网格划分相对稀疏.橡胶球体有限元模型共有单元70 345个，节点46 330个.

图3 有限元网格模型Fig.3 Finite element mesh model

设置静载荷大小为50 N，方向为y轴正向.设置压力分布为橡胶球内表面，分别仿真得到不同内压作用下的橡胶球体变形结果如图4所示.进一步改变静载大小，充气球刚度仿真结果如图5所示.

从图中可以看出，球体刚度受流固耦合作用，具有明显的非线性.在气压达到一定的程度后，结构刚度也基本保持定值，由此确定压力的安全有效作用区间为0～3.0 MPa.

2 动力学建模

本文研究大型空间碎片的机械脉冲主动消旋方式，柔性末端尺寸要远小于空间碎片的形貌尺寸，简化空间碎片的接触表面为平面.建立动力学模型如图6所示，kn和cn分别为等效法向刚度和法向阻尼，kt和ct分别为等效切向刚度和阻尼，P为初始压强，P′碰撞后压强，v0表示末端执行器的初始碰撞速度.

图4 静载位移仿真结果Fig.4 Simulation results of displacement

图5 充气球刚度与压强关系Fig.5 Relationship of stress and pressure

图6 接触力模型Fig.6 Contact force model

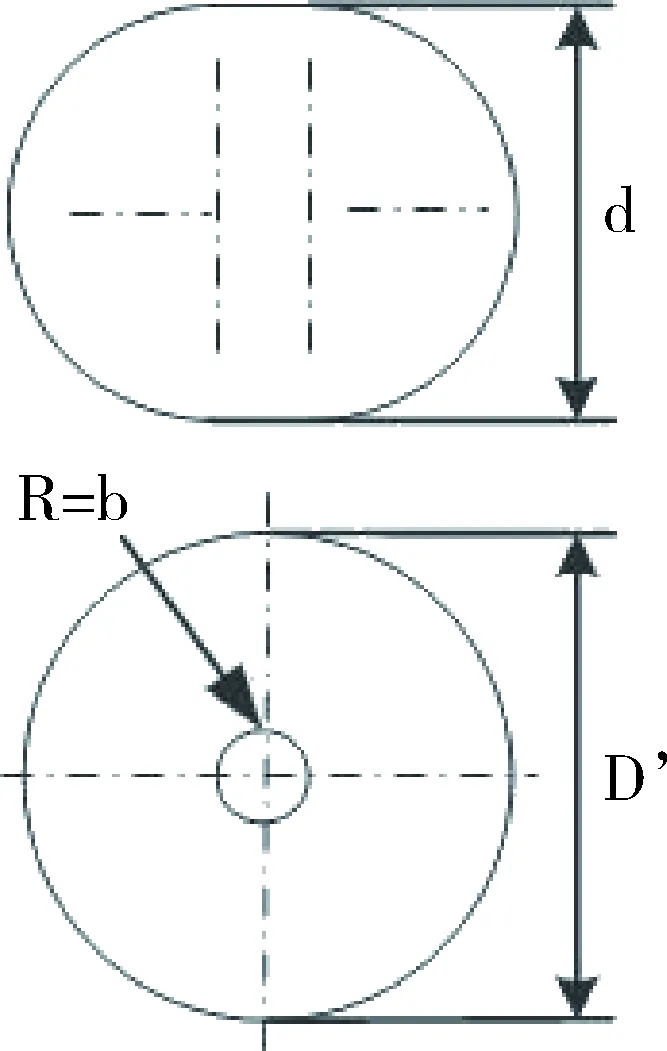
图7 充气截面构型变化Fig.7 Section structure change

2.1 计算法向碰撞力

基于Hertz接触理论，计算两个构件之间的接触力，一是两个构件之间相互嵌入而产生的弹性力Fn，二是由于相对速度产生的阻尼力Fc，更加接近于实际的碰撞情况.假定空间碎片为刚性，且柔性末端只产生弹性变形，推导时基于以下假设：(1)气体为等温气体，(2)膜材截面周长不变，如图7所示.

当柔性末端与空间碎片发生碰撞时，设静载下充气球的下压量为δ，则压缩后截面高度d=D-δ，接触面半径为b.根据截面周长不变假设有：

(2)

(3)

变形后体积为：

(4)

基于等温假设，由压强与体积的关系得：

(5)

根据充气球接触部分的力平衡关系得：

Fn=P′πb2

(6)

由Hunt Crossley阻尼模型，阻尼力为：

(7)

阻尼系数为：

(8)

其中：e为材料的恢复系数，v0为撞击的初始相对速度.

综上所述，法向接触力计算公式为：

F=Fn+Fc=

(9)

2.2 计算切向摩擦力

与金属的摩擦行为不同的是，橡胶在滑动摩擦过程中摩擦系数受温度、载荷等诸多因素的影响并不是一个常数.橡胶属于弹性模量很低、粘弹性很高的高分子聚合物，但其摩擦特性仍可以用 Coulomb 模型来描述.对于橡胶的摩擦特性可以用下式准确地描述为[12]：

f=Fadh+Fhyst=

(10)

其中,F为载荷，σ0为拉伸强度，K为常数，pr为真实接触压力，pc为轮廓接触压力，E*为复合弹性模量，tanδ为损耗因子.

上述分析了一下橡胶摩擦力的两大组成要素，粘附摩擦力和滞后摩擦力：Fadh为接触表面间因粘着的不断产生与破坏作用而产生的粘附摩擦力，粘附现象实质上属于表面效应，粘附摩擦力也属于表面力；Fhyst为接触表面不平整引起橡胶周期性变形而产生的滞后摩擦力.橡胶的滞后摩擦力属于体积力，源于橡胶材料滑动过程中的变形.

3 实验系统

为开展变压力柔性末端与空间碎片碰撞的动力学分析，设计了碰撞力测量系统图8所示.

图8 实验原理图Fig.8 Schematic diagram of impact

实验系统主要包括冲击装置，碰撞力采集装置，信号数据采集仪，计算机及附属元件等部分.整个碰撞力测量过程所用到的实验装置实物如图9所示.

图9 实验装置实物图Fig.9 Test devices of impact

4 仿真与试验

4.1 有限元仿真

现设置初始碰撞速度方向沿y轴正方向，滑移速度方向沿x轴负方向，大小为0.1 m/s，分别仿真得到不同内部压力作用下的橡胶球的应变结果如图10所示.

图10 滑移仿真结果Fig.10 Simulation results of sliding displacement

进一步改变内部压强进行多组仿真，根据力平衡关系求得碰撞力变化曲线如图11所示.

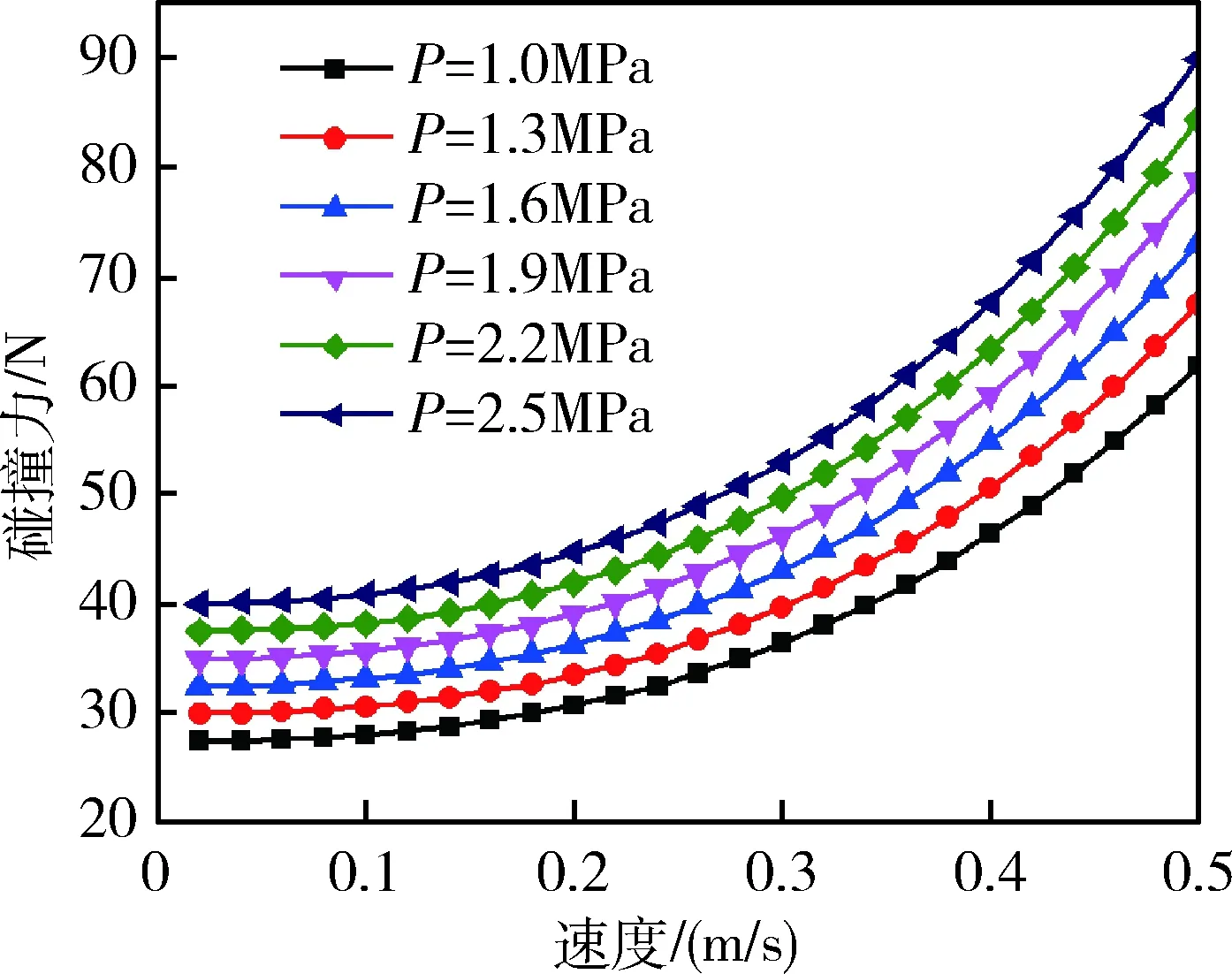
图11 碰撞力变化Fig.11 Change of force

4.2 单自由度冲击实验

实验时，采用单一变量原则，初始碰撞速度为0.4 m/s，调节比例阀，向柔性末端内部充气，改变橡胶球体内压分别为1.0 MPa、1.5 MPa、2.0 MPa、2.5 MPa，得到碰撞力如图12所示，其中碰撞力峰值分别48.519 N、54.669 N、62.857 N和69.183 N.

图12 碰撞力与压强关系Fig.12 Relationship of force and pressure

由图可见随着内部压力的不断升高，柔性末端与压板之间的碰撞力不断增大，即机械冲击效果越明显.实际冲击力存在加载和卸载过程.对比碰撞力理论计算和仿真实验结果如图13所示.对比数据如表2所示，其中计算误差小于6.7%.

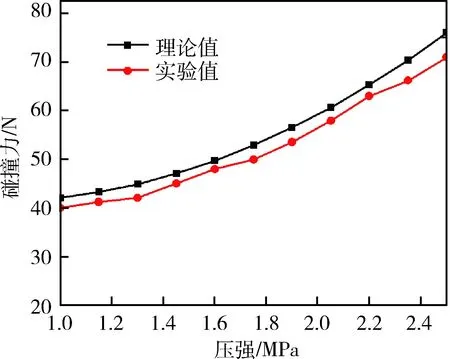
图13 碰撞力数据对比图Fig.13 Force comparison results

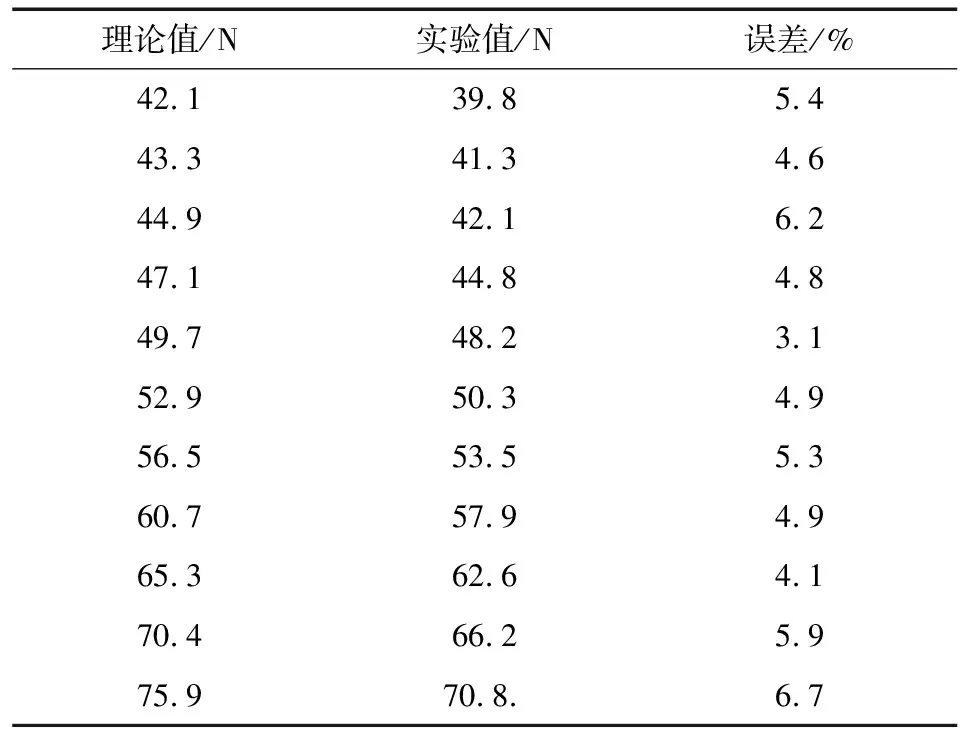
表2 碰撞力数据对比Tab.2 Collision force data comparison

其次，控制机械臂在接触面滑动，初始碰撞速度为0.4 m/s，调节比例阀，向橡胶球体内部充气，改变内部压强，得到滑动摩擦力实验结果如图14所示.其中实际摩擦力与正压力正相关，但是摩擦系数并非常数，计算摩擦力与实际摩擦力的计算误差为22.6%，不符合控制精度求.

图14 摩擦力数据对比Fig.14 Friction comparison results

4.3 实验结果分析

实验表明滑动过程中橡胶球体积发生滑移变形如图15所示.从而产生一个摩擦力f，它有阻止滑动的效果：

fdisp=(a+aexp(bs)[csinh(ds)-ecosh(ds)])F

(11)

其中,s为滑动位移，F为载荷，各个系数又可以通过实验数据进行公示拟合：

(12)

图15 滑动变形结果Fig.15 Results of sliding deformation

综上，修正后的摩擦力计算公式如下：

(13)

得到摩擦力的实际值，理论值和修正后计算值之间的对比如图16所示，对比数据如表3所示，误差小于6.9%.

图16 修正摩擦力数据对比Fig.16 Corrected friction comparison results

表3 摩擦力数据对比Tab.3 Friction data comparison

对比分析可知，修正后的摩擦力计算模型考虑到充气球结构在滑动过程中的大变形，变形导致接触面积增大，这也符合实际的摩擦力计算方法，因此较初始理论计算值增大，更加接近理论计算值，数值趋势吻合较好.

5 结 论

本文采用变压力柔性冲击末端为主体研究对象，通过有限元仿真对结构参数进行了优化.考虑冲击过程中充气球结构的流固耦合效应，对柔性末端的材料刚度进行了识别，确定了压力阈值.建立了包含法向碰撞力和切向摩擦力的非线性冲击力模型，搭建了碰撞力测量实验系统，开展单自由度冲击实验，验证法向碰撞力模型，修正切向摩擦力模型.对比分析，法向碰撞力计算误差小于6.7%，切向摩擦力计算误差小于6.9%，满足空间碎片主动消旋控制精度要求.后续研究将通过在软体橡胶小球表面制备各种各样的微纳米结构增大摩擦系数，利用等离子体加工改变橡胶球表面的界面能.开展微重力环境下的多自由度冲击实验，验证变压力柔性冲击末端的消旋效率.