基于双磁偶极子的螺线管磁场建模分析

谢阳光，李清华，解伟男，李新年

（1.中国航空工业集团公司 西安自动飞行控制研究所，西安 710065；2.哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150001）

近年来，随着经济的不断发展，人们对导航定位的需求不断提高，然而，在复杂的环境，如地下、室内等，由于GPS信号较弱的穿透力，导致用户常常接收不到位置信号，而惯性导航会产生误差积累[1]，同样不适合长时间使用，因此需要提供一种稳定、可靠、无累积误差的高精度定位方法。低频交变磁场拥有穿透力强，误差不会随时间累积等优点[2-4]，在提供复杂环境下的定位服务上展现了巨大的潜力。低频交变磁场通常由螺线管产生，为了获得位置信息，往往需要利用目标位置的磁特征量之间的相互关系。因此螺线管的磁场分布建模是低频交变磁场定位的关键技术，在定位解算中发挥着重要的作用。

研究表明，单磁偶极子模型在远场能够保持较高的精度[5]，但是在近场时，误差明显增大。为了得到电机中圆柱永磁体精确磁场分布模型，Hungsun等[6]在研究了DMP等效法和单磁偶极子等效法的基础上，提出将永磁体等效为排列规则磁偶极子阵列，并根据永磁体特性设置目标函数和约束条件，进而确定和优化模型参数，仿真证明该方法能够有效提高磁场模型的精度。戴忠华等[7]通过分析磁偶极子等效磁矩的收敛性，得到了磁性物体单磁偶极子模型的适用条件，在2.5倍磁体长度以外的空间，使用单磁偶极子模型近似磁性物体，才能保证较高的精度。

为了解决在近场条件下，单磁偶极子模型误差较大导致的低频交变磁场的定位精度低的问题，本文提出了一种基于双磁偶极子的螺线管磁场分布模型。首先利用对称的两个磁偶极子阵列来模拟螺线管的磁场分布，然后将复杂的求解磁矩过程转换为利用模拟退火算法获取最优模型结构参数。为了降低模型用于定位解算时的复杂度，将磁偶极子阵列简化为磁偶极子，最终得到了易于定位解算的双磁偶极子模型。

1 螺线管磁场分布建模

1.1 磁偶极子阵列模型

在研究磁性物体的磁场分布时，通常将其等效为一个或多个磁偶极子单元的组合。磁偶极子是磁场研究的基本单位之一，可以将磁偶极子近似看作半径为R的圆形载流回路[8]。设环境中的磁导率为μ0，圆形载流回路的电流为I，则根据毕奥-萨伐尔定律，如图1所示，中心高度为h的磁偶极子在空间中任意一点P(r,φ0,θ0)处，产生的磁感应强度三轴分量的表达式如式(1)所示：

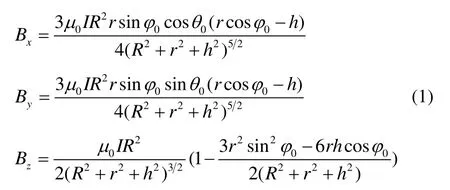
其中，r为目标点P到坐标原点O的相对距离，φ0为俯仰角，θ0为相对方位角[9]。

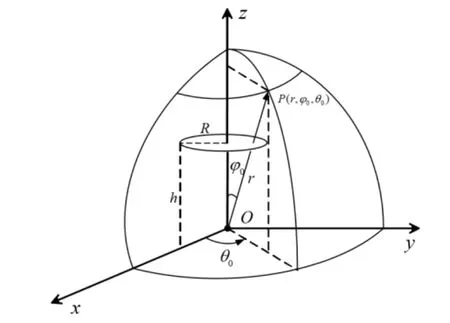
图1 磁偶极子模型Fig.1 Magnetic dipole model

由铁磁学理论可知，磁体的磁性是由大多数磁性单元的磁矩方向趋向一致而产生的，因此在磁矩收敛的条件下，这种一致性共同作用的磁场能够等效为一个总磁矩产生的磁场。传统的单磁偶极子模型的原理就是将螺线管等效为一个在螺线管中心位置的圆形磁偶极子，数学表达式如式(2)所示，其中M为等效磁矩的大小。螺线管实物图如图2所示，由于螺线管的物理原因，在靠近螺线管的区域，不能简单利用磁偶极子来等效[10-11]，因此传统的单磁偶极子模型在近场并不适用。为了解决近场精确定位问题，本文利用多个磁矩已知、排列规律的磁偶极子来建立螺线管磁场分布模型。

图2 双轴螺线管Fig.2 Dual-axis solenoid

磁偶极子阵列模型的结构如图3所示，将螺线管等效为关于xoy平面对称的两个磁偶极子阵列，其中原点O为螺线管的中心。每个磁偶极子阵列有等距排列的k层，各层之间的间隔为d1。每层有同心的n个磁偶极子，如图4所示，相邻磁偶极子的半径相差d2。因此初始设定好d1、d2，则只需要通过调整k和n，就能得到不同结构的磁偶极子阵列模型。

根据式(1)可知，当磁偶极子阵列模型的参数k和n已知时，可以计算出磁偶极子阵列模型在目标位置P(r,φ0,θ0)产生的磁感应强度Bn，其三轴分量如式(3)所示：

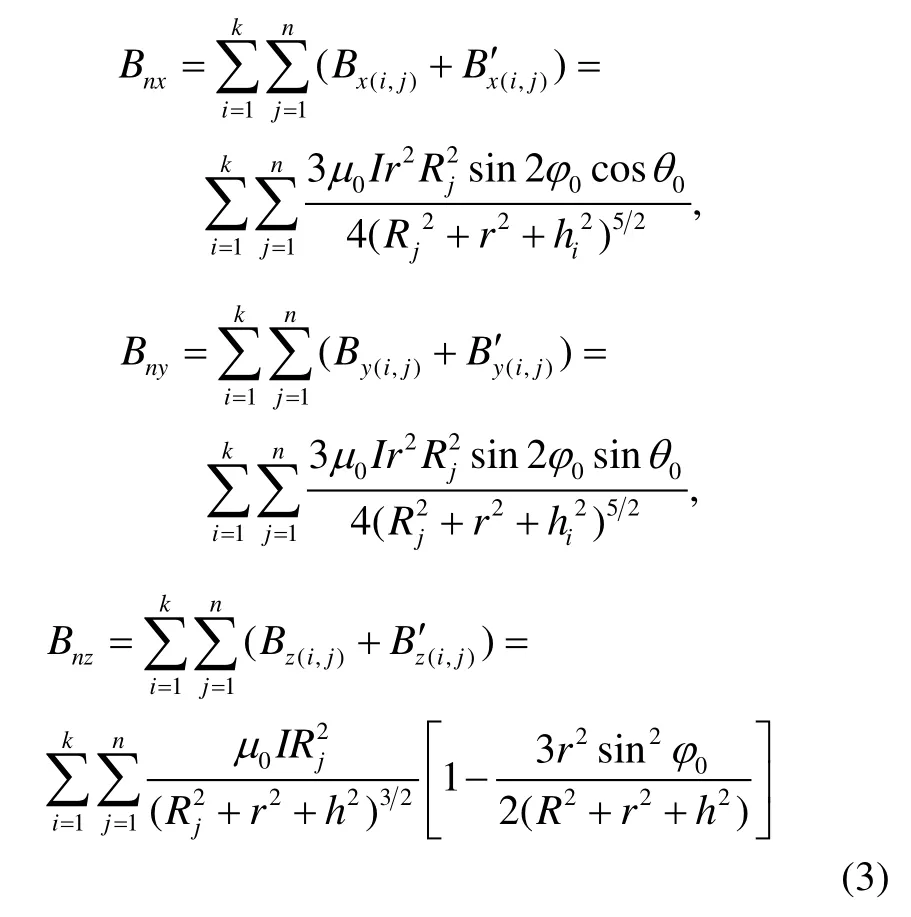
式中，Bx(i,j)为上方的磁偶极子阵列的第i行、第j列个磁偶极子在目标位置产生的x轴方向磁场，Bx′(i,j)为下方的磁偶极子阵列的第i行、第j列个磁偶极子在目标位置产生的x轴方向磁场，其余同理；hi为磁偶极子阵列中第k行磁偶极子相对于原点的高度绝对值，有hi=h0+(i- 1)d1，h0为磁偶极子的基准高度；Rj为磁偶极子阵列中第n列磁偶极子的半径，有Rj=R0+ (j- 1)d2，R0为磁偶极子的基准半径。

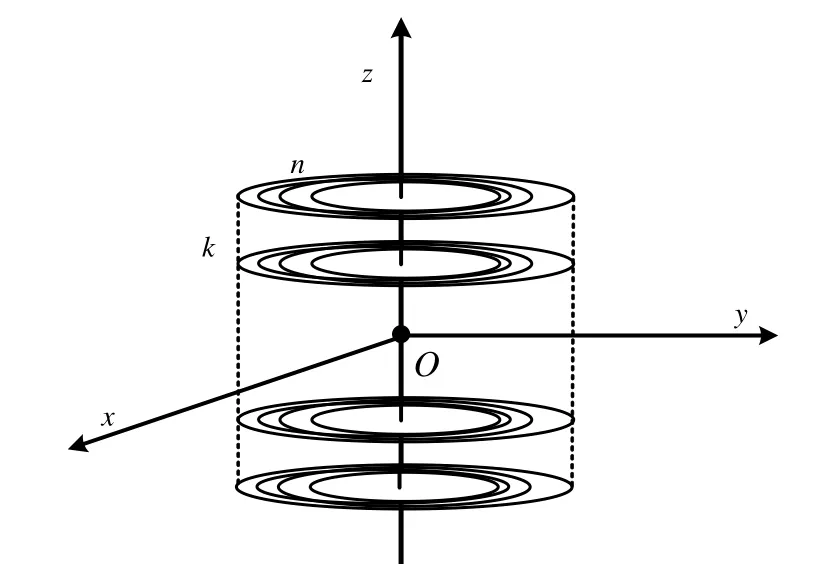
图3 磁偶极子阵列模型Fig.3 Magnetic dipole array model

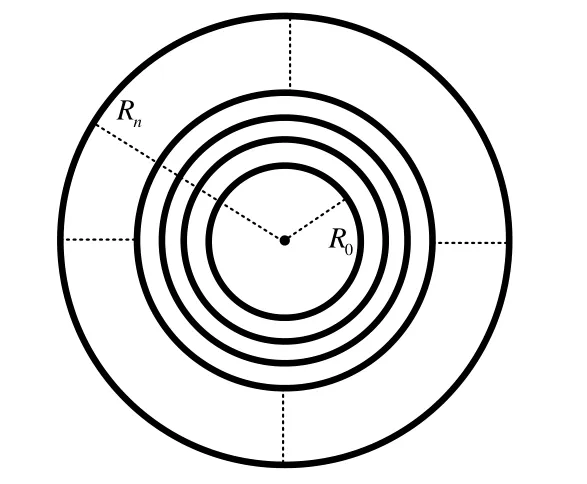
图4 磁偶极子阵列横截面Fig.4 Cross section of magnetic dipole array

设磁通门传感器在目标位置测得的磁感应强度为Bm。定义磁偶极子阵列模型在某已知点产生磁场的相对误差e为：

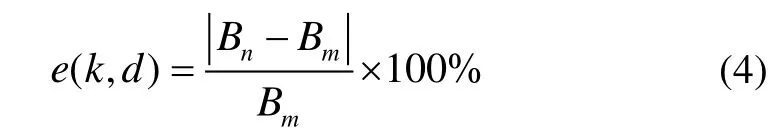
为了提高模型的精度，防止模型过拟合，可以利用多个点的相对误差均值E作为目标函数：

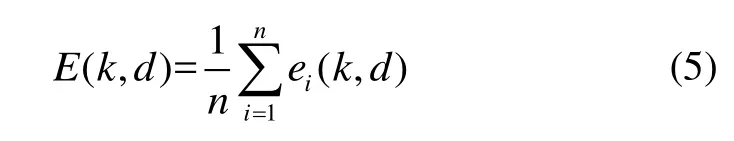
为了最小化目标函数，得到最优的磁场分布模型，可以利用模拟退火算法对模型进行优化。具体步骤如下：

① 设置初始模型参数为 (k0,d0)，并令其为当前最优解。设初始退火温度为T0，最小温度为Tmin，衰减系数为α以及每个温度下的迭代次数为L；

② 从当前的最优解(kn,dn)开始进行迭代，在当前最优解的邻域随机产生新解 (kn+1,dn+1)，然后计算其对应的目标函数值E(kn,dn)，进而能够得到当前目标函数值增量 ΔE=E(kn+1,dn+1)-E(kn,dn)；

③ 如果ΔE＜0，则接受新解 (kn+1,dn+1)作为当前温度Tn下的最优解，否则将以概率P= e xp(- ΔE/T)接受该解作为当前最优解；

④ 判断当前最优解的目标函数值是否满足模型的精度要求，如果满足则输出当前最优解为最优模型参数，否则，继续搜索新解；

⑤ 重复进行步骤②～④，当迭代次数达到L时，利用衰减系数α进行退火操作，使得Tn+1=αTn，然后继续进入迭代过程。当目标函数满足精度要求或温度达到最小温度Tmin时，停止迭代，当前最优解记为最优模型参数。

相对于其它的优化方法，模拟退火算法的优点是其优化结果与初始值设置无关，然而为了进一步提高算法的速度，可以根据螺线管的规格，使设定的初始模型参数 (k0,d0)接近真实模型。

1.2 双磁偶极子模型

低交变磁场定位的原理是根据目标位置测得磁感应强度特征量[12-14]，利用磁场分布模型解算出位置信息，因此需要将磁偶极子阵列模型的数学表达式进行简化。由图3可知，在磁偶极子阵列模型中，各个磁偶极子排列规则，所以可以将两个磁偶极子阵列各自等效为一个磁偶极子，得到如图5所示的双磁偶极子简化模型。

简化后的双磁偶极子模型在空间中任意点产生的磁感应强度三轴分量如式(6)所示：

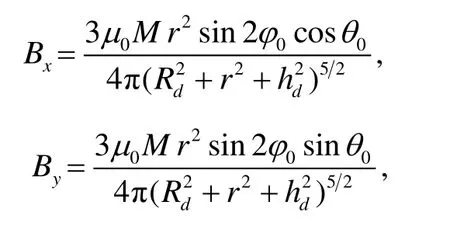
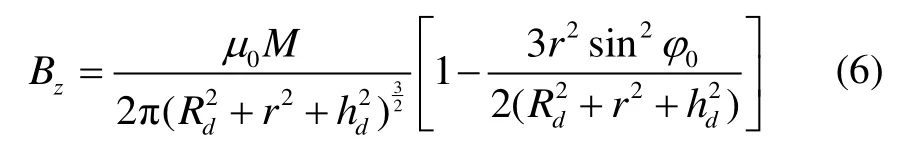
式中：M为磁偶极子的磁矩，可以用线圈磁矩M = N ⋅ I⋅ S 来描述，N为线圈匝数，S为等效电流环的面积，有 S =πRd2； Rd和 hd分别为简化后磁偶极子的半径和中心所在的高度。

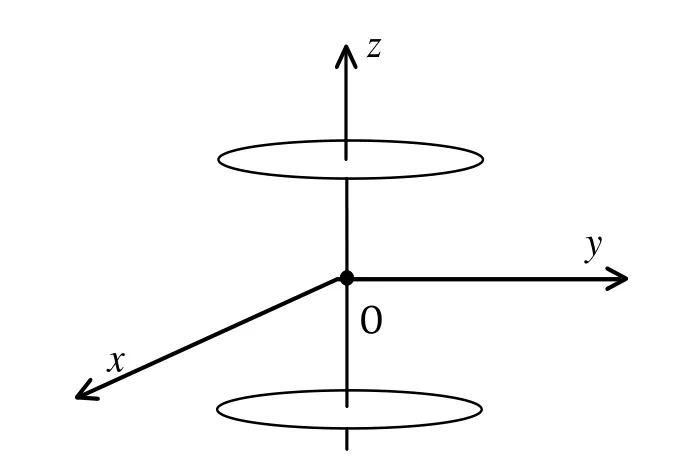
图5 双磁偶极子模型Fig.5 Dual magnetic dipoles model

磁偶极子阵列模型的横截面示意图如图4所示，其中，R0为磁偶极子的基准半径，Rn为第n列磁偶极子的半径。由于磁偶极子的半径和高度远远小于目标位置到原点的距离r，则由式(3)可知，当目标点确定时，磁偶极子阵列模型在三轴方向上产生的磁感应强度与近似成正比，且受hj的影响较小。因此双磁偶极子模型中，磁偶极子的半径 Rd为磁偶极子阵列模型中任意一行上n个磁偶极子半径的均方根值，高度 hd可以设为任意一列上k个磁偶极子中心高度的平均值，即：

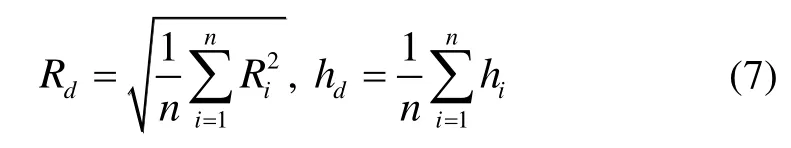
为了确定双磁偶极子的等效磁矩，还需要确定模型简化后磁偶极子的等效匝数。由于在简化数学表达式的过程中，对参数做了近似处理，因此如果直接令等效匝数为磁偶极子阵列中的磁偶极子数N = k ⋅ n，会导致简化后的模型精度下降，因此可以设置阈值ε，通过遍历N的ε邻域，返回使得目标函数E最小化的参数N，得到磁偶极子的磁矩M。将 Rd、 hd、 M带入

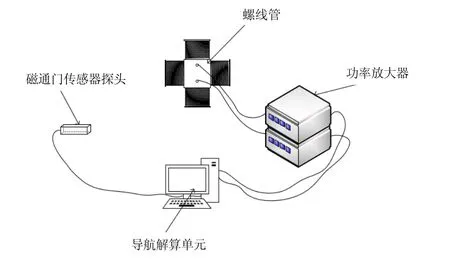
图6 实验系统结构图Fig.6 Experimental system schematic structure

式(6)，得到基于双磁偶极子的螺线管磁场分布模型。实验系统结构图如图6所示。

1.3 基于三角函数拟合的信号辨识方法

由于环境中存在着诸多干扰磁场，包括地磁场、工频磁场等，磁通门传感器采集到的三轴磁场均不能直接用于螺线管磁场模型评估，需要采取措施抑制干扰，提高磁场的测量精度。

一种可行的方法是利用三角函数拟合对磁场信号进行辨识。向螺线管中通入正弦电流，由式(3)可知，在空间中任意位置能够产生正弦变换的磁场信号，则磁通门传感器x轴采集到的磁场信号可以表示为：

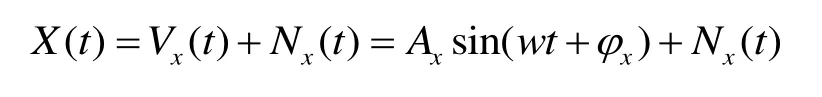
其中，Bx(t)为待检测信号，Nx(t)为噪声信号，Ax和φx分别为螺线管激磁信号幅值和相位，设参考信号为：

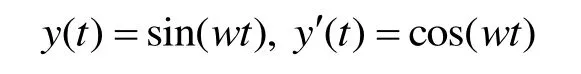
则根据相关原理，对于一个正弦信号周期T内的N个测量数据有：

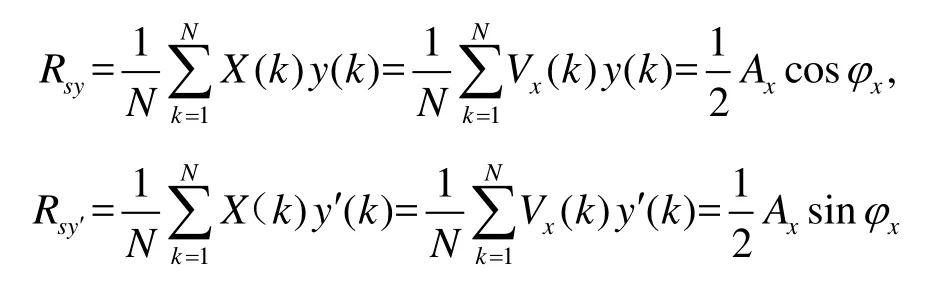
因此，辨识出的正弦信号参数为：

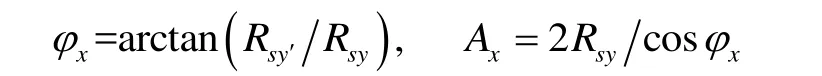
同理，对传感器另外两个轴向采集到的数据进行信号辨识，最后，能够得到准确的三轴磁场幅值，则在该点由螺线管激磁产生的总磁场强度为：

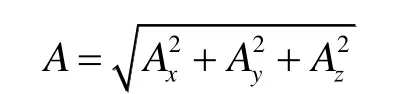
将经过信号辨识后的测量数据带入模拟退火算法进行模型参数优化，能够进一步提高磁场分布模型的精度。

2 实验验证

本节分别使用单磁偶极子模型、磁偶极子阵列模型、双磁偶极子模型对同一螺线管的磁场分布进行建模。实验系统如图7所示，本实验使用的螺线管，轴向长度为35 cm，直径15 cm，铜线的电阻为4 Ω。实验所采用的传感器为西安华舜公司生产的三轴磁通门传感器，分辨率0.1 nT，线性度≤0.01%。为了提高磁场测量的精度，向螺线管通入频率为2 Hz，幅值为3 A的电流，因此目标位置的磁场由频率为2 Hz的正弦磁场和干扰磁场组成，利用三角函数拟合技术，对磁通门传感器采集到的磁场数据进行辨识，得到在目标位置精确的螺线管激磁产生的总磁场强度。

图7 实验系统Fig.7 Experimental system

为了考察模型在不同区域的有效性，在空间中分别选取了近场和远场两组测量点集。首先，分别考察三种模型在远场条件下的效果，验证结果如表1所示。可以发现当测量点远离螺线管时，三种螺线管磁场模型都能够保持较高的精度，其中，单磁偶极子模型的最大相对误差只有 4.66%，磁偶极子阵列模型的最大相对误差为 3.34%，双磁偶极子模型的最大相对误差为3.38%。

然后，验证三种模型在近场条件下的效果，结果如表2所示。可以发现当测量点靠近螺线管时，传统的单磁偶极子模型误差明显增大，在测量点上的最大相对误差达到了25.67%，而磁偶极子阵列模型和对其简化后的双磁偶极子模型仍然保持了较高的精度水平。其中，磁偶极子阵列模型的最大相对误差为3.79%，双磁偶极子模型的最大相对误差为3.84%。磁偶极子阵列模型简化成双磁偶极子模型后，精度基本保持一致，证明简化后的模型能够很好的描述螺线管在全区域的磁场分布。

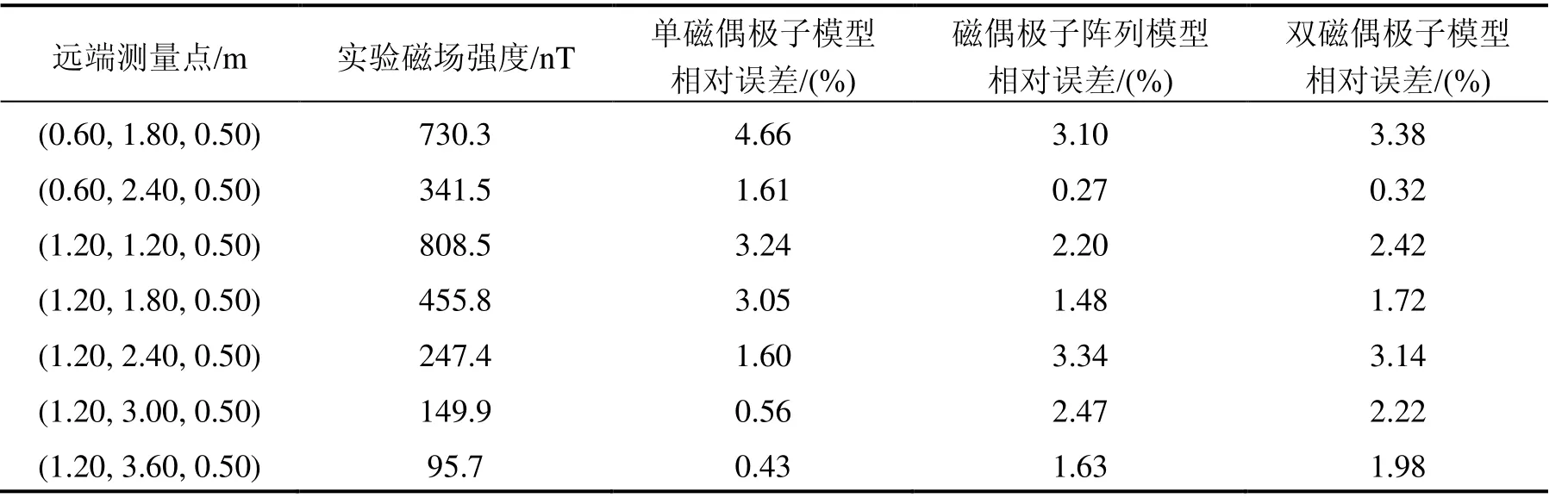
表1 远场下模型的验证结果Tab.1 Validation results of the model in remote-field

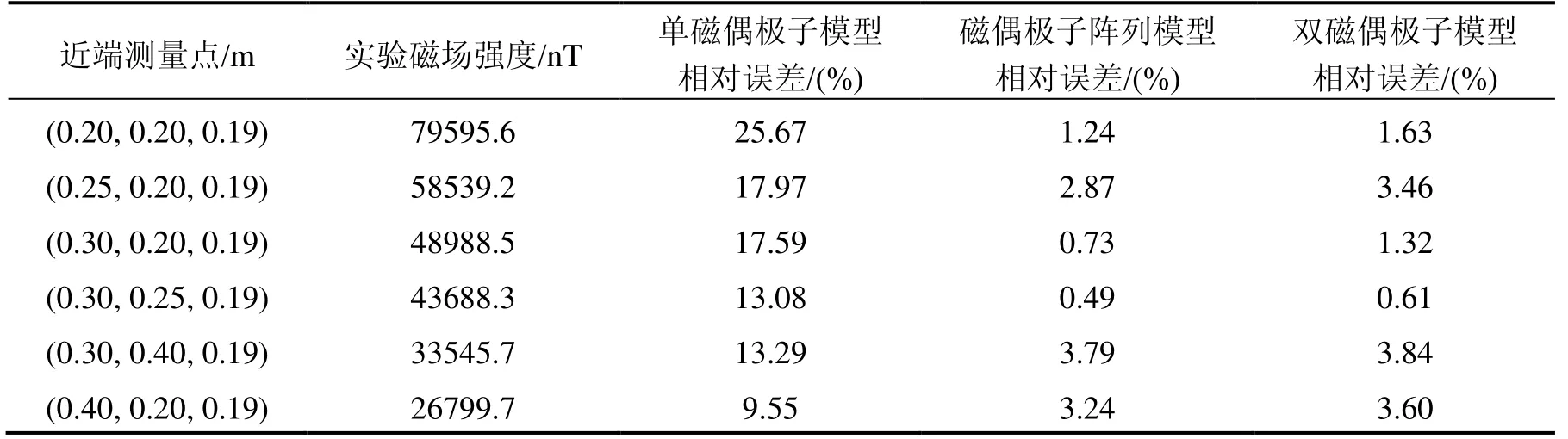
表2 近场下模型的验证结果Tab.2 Validation results of the model in near-field

最后，考察近场条件下，不同螺线管磁场分布模型的定位精度。由式(6)可知，双磁偶极子模型在空间任意点产生的磁感应强度在xoy平面上的投影满足式(8)：

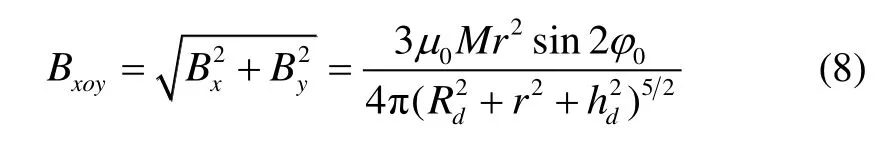
式中，Rd、 hd、M都为已知的双磁偶极子模型参数。同理，由式(2)可知，单磁偶极子模型在空间任意点产生的磁感应强度在xoy平面上的投影满足式(9)：

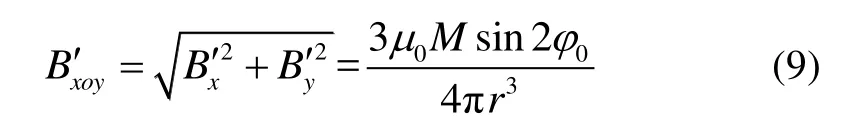
由式(8)(9)可知，若已知测量点的俯仰角φ0，则可利用磁通门传感器测得的x轴方向和y轴方向的磁感应强度解算出测量点到原点的距离。实验结果如图8所示，能够明显看出，在近场条件下，使用双磁偶极子模型定位的精度相对单磁偶极子模型的精度，有较大提高。由图8可知，双磁偶极子模型的最大定位误差为0.003 m。

根据以上的实验结果可以看出，在近场条件下，相对传统的单磁偶极子模型，双磁偶极子模型具有更高的精度，能够更加准确地描述螺线管的磁场分布，进而提高了近场区域低频交变磁场定位的精度。

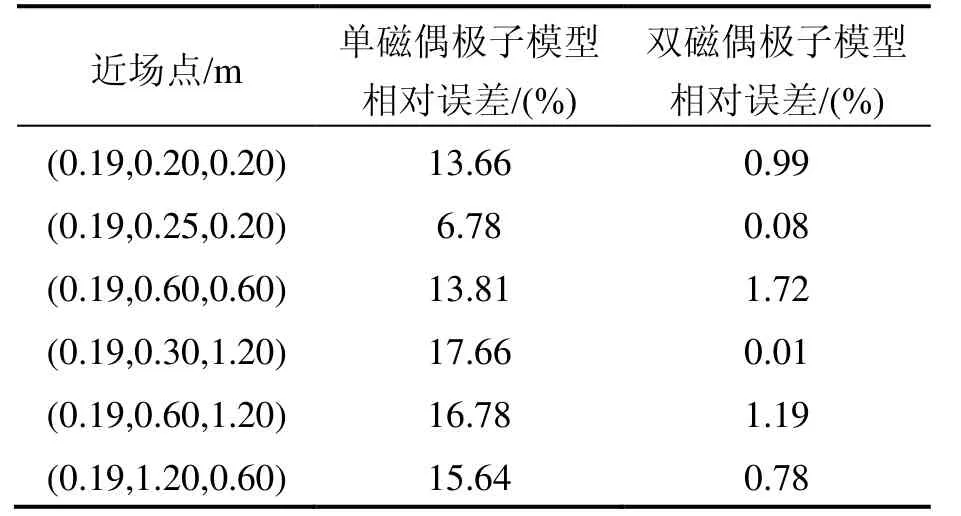
表3 近场条件下模型的定位结果Tab.3 Position results of the model under near-field

图8 定位误差曲线Fig.8 Positioning error curve

3 结 论

针对低频交变磁场定位的螺线管磁场分布建模问题，本文提出了一种基于双磁偶极子的建模方法。该方法首先将螺线管等效为排布规律的磁偶极子阵列，利用模拟退火算法搜索最优模型参数，来拟合螺线管的磁场分布，提高了模型的精度。在磁偶极子阵列模型的基础上，本文将其简化成了两个对称的磁偶极子，最终得到了易于位置解算的双磁偶极子模型。

实验结果表明：单磁偶极子模型在远场最大相对误差为4.66%，在近场最大相对误差为25.67%；双磁偶极子模型在远场的最大相对误差为 3.38%，在近场区域的最大相对误差为 3.60%，证明双磁偶极子模型保持了单磁偶极子模型远场精度高的同时，进一步提高了近场的精度。同时在近场区域时，利用双磁偶极子模型定位的最大定位误差相比单磁偶极子模型最大定位误差下降了90.26%。因此，本文提出的基于双磁偶极子的建模方法能够有效地改善螺线管磁场分布模型，提高近场区域低频交变磁场定位精度。