“机场的出租车”选择问题决策模型研究

周步芳 付维杰 乔亚琴

摘  要：文章对2019年“高教社杯”全国大学生数学建模竞赛C题“机场的出租车”选择问题，提出相应策略。首先，建立非线性决策模型，为确保司机收益最大化提供方案;其次，将咸阳机场数据代入模型中计算得到出租车司机决策方案;然后，建立排队论模型并优化，为助管理部门设置合理上车点提供方案，提高乘客乘车效率;最后，建立匹配算法中的几何算法模型解决长短途出租车的收益均衡问题。最后给出模型的评价。

关键词：非线性模型;排队论模型;几何算法;数学建模

Abstract：In this paper，the paper puts forward the corresponding strategies for the C-question of “Airport Taxi” in the national college studentsmathematical modeling contest of 2019 “Higher Education Society Cup”. Firstly，a nonlinear decision-making model is established to provide a scheme for maximizing the drivers income;secondly，the Xianyang Airport data is substituted into the model to calculate the taxi drivers decision-making scheme;then，the queuing theory model is established and optimized to provide a scheme for the management department to set up a reasonable boarding point and improve the passengers riding efficiency;finally，the geometric algorithm model solution in the matching algorithm is established to solve the problem of income balance of long and short distance taxi. Finally，the evaluation of the model is given.

Keywords：nonlinear model;queuing theory model;geometric algorithm;mathematical modeling

0  引  言

当前高等教育着重培养具有高素质的专业技能应用型人才。“机场的出租车”选择决策模型研究，是通过数学建模将数学知识应用于实践，把实际问题抽象特征用数学公式量化求解。对该问题的研究，有助于教师在高等数学教学中渗透数学建模思想，有效将数学知识与应用能力结合，为社会培养具有一定创新意识、创新思维能力的高层次人才。文章以咸阳国际机场为研究背景，通过分析咸阳国际机场出租车数据，建立基于“机场的出租车”选择问题的数学模型，并对模型优化处理，以期为全国机场出租车司机提供合理的选择方案，即为出租车司机提供使得收益最大化的决策方案。

1  拟解决的问题

“机场的出租车”选择决策模型研究问题背景：在公共交通便利的今天，人们对于出行有了更高的要求。选择航空出行的人也越来越多，使机场成为重要的交通枢纽，出租车是从机场到市区的主要的交通工具之一。但出租车从市区载客到达机场后，有两种选择，即在蓄车池排队载客进入市区或者空车返回市区，并且两种选择付出成本不同：载客返回需要付出一定时间成本，排队等待也存在相应风险;空载返回将要付出空载费用且有可能失去潜在的载客收入。因此，机场出租车问题研究对机场交通流畅以及经济发展有重要的作用。现拟解决以下四个问题：

问题1：研究影响司机决策的因素、司机收入与乘客数量变化的规律，为司机提供相应选择策略。

问题2：根据问题1的模型给出国内咸阳机场出租车司机决策方案。

问题3：在机场拥有两条并行车道，分别对经常出现的乘客排队乘车和出租车排队载客的情况，帮助管理部门提供设置上车点的方案，保证乘客乘车效率最高。

問题4：假设出租车的收益受载客行驶里程影响，乘客到达目的地远近不同，出租车允许往返载客但不可选择乘客也不能拒载。有关部门对短途载客返回的出租车给予一定优先权，试提出“优先”安排方案，使长短途出租车收益平衡。

2  问题分析

2.1  问题1分析

影响出租车司机收益的因素很多，机场的客流量是一个主要因素，季节不同、时间不同，则机场客流量不同。依此，将机场客流量分为高峰期和低峰期。假设低峰期客流量小司机选择空返，高峰期客流量大载客返回不用排队等待。对问题1，建立非线性规划模型，计算蓄车池内车辆数n为何值时出租车选择策略最优。

2.2  问题2分析

利用问题1建立的模型，以国内咸阳机场的数据为例，通过MATLAB计算蓄车池内车辆数n，得到司机收益值，比较不同方案收益的大小，让出租车司机做出准确的判断。

2.3  问题3分析

考虑乘客到达乘车台的时间符合泊松分布，上客时间符合负指数分布，针对问题3设计了3个排队论模型，分别是M/M/1/∞/∞/FCFS模型、M/M/C/∞/∞/FCFS模型和M/D/1/∞/∞/FCFS模型。

2.4  问题4分析

针对问题4，建立几何算法模型，并通过GPS定位，对每辆返程出租车的电子路程进行判断，确定“优先”安排方案，最终达到长短途出租车收益均衡。

3  模型的建立与求解

3.1  问题1模型的解决方案

设蓄车池的车辆数为n，出租车司机每天工作时间为H，乘客上车时间为t。假设：（1）司机从排队到载客返回市区的时间等于从市区到机场排队区的时间，记为Z;（2）从市区到机场和机场到市区的价格设为R;（3）出租车在蓄车池依“先来后到”原则排队等候载客。则高峰期司机获得收益的非线性规划模型（A方案 ）为：

3.2  问题2的解决方案

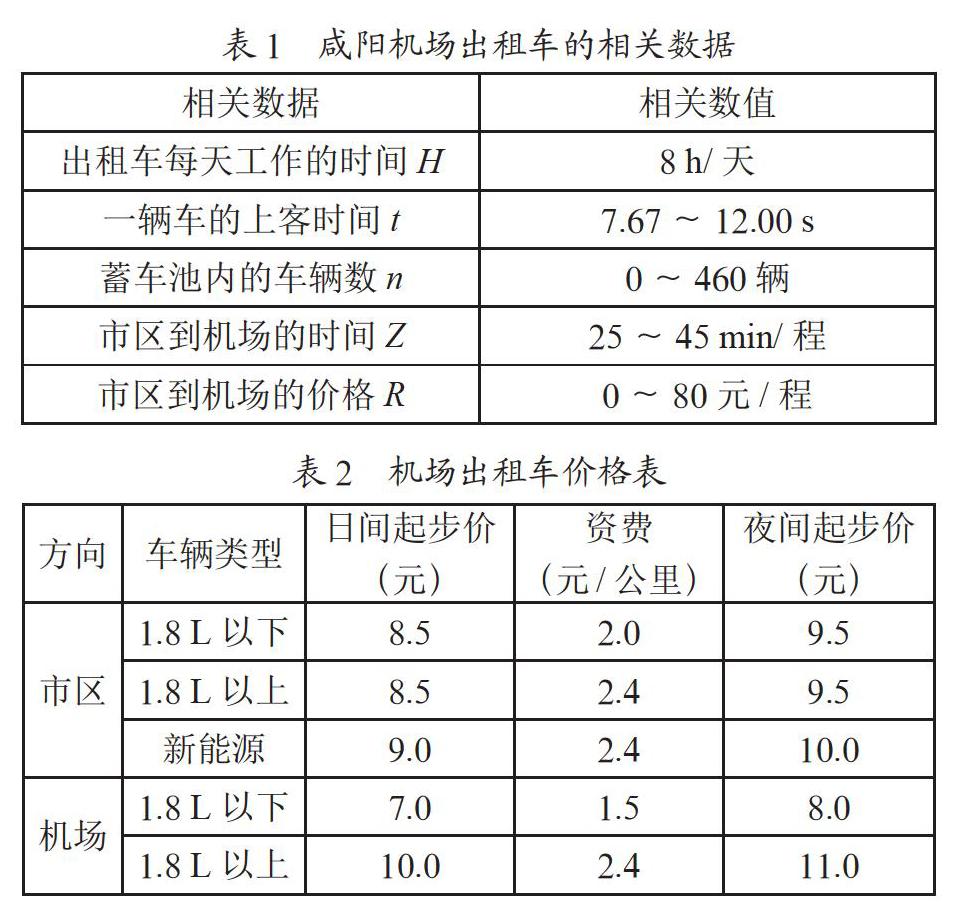
如表1是国内咸阳机场出租车相关数据，表2是出租车价格标准。此外，车型1.8 L以上（含新能源）2公里、1.8 L以下3公里按起步价收费，乘客需额外支付过桥路费，夜间23：00—06：00之间价格上调0.3元。表2中车程8公里以内按计费价格收费，8公里以上开始计空贴，空贴比例是公里运价的50%。司机每日工作时间按照国家标准工作时长8小时来计算，由参考文献[1]知乘客上车时间为7.67 s ～12.00 s，机场到市区行车时间约为25 min～45 min，由参考文献[2]知机场蓄车池最大蓄车量约为460辆。表中的实验数据来源于咸阳国际机场官网。

通过问题1建立的模型，将表1、表2的数据代入式（1）与式（2），利用MATLAB计算蓄车池内车辆数n，得到图1、图2的收益与蓄车池内车辆数n之间的关系。

由图可知蓄车池车辆数n越大司机收入越少，蓄车池车辆数n越小司机收入越多。将以上数据代入式（1）与式（2）中计算，可得当n为0～125时司机选择进入蓄车池排队载客获利更高，当n为125～352时司机选择放空返回和排队载客的收益持平，当n大于352时司机选择返回市区更佳。

3.3  问题3的解决方案

为使机场交通畅通，保证乘客和车辆安全的情况下使乘车效率最高，在有两条并行车道的前提下，建立排队论模型，设置合理的出租车上车点，并不断进行优化、改进，最终使乘车效率最高。排队系统模型[3]被广泛应用于窗口服务、交通运输、网络服务等问题的研究。如图3所示是该模型的排队流程。

假设随着信息技术的发展，机场蓄车池有较规范的管理模式，整个蓄车池运行状况良好。乘客下飞机后依次进入蓄车池排队上车，图4给出最基本的排队形式。但是没有专门的等候区域，是不能保障乘客秩序的。因此，引入取号机引导乘客进入排队区等候，并且在乘客取票时，服务人员利用信息手段配合取票过程，使取票窗口的效率提升，得到图5所示的优化模型。

排队设计了3个排队论模型，M/M/1/∞/∞/FCFS模型，M/M/C/∞/∞/FCFS模型和M/D/1/∞/∞/FCFS模型。表4是乘车排队窗口不同模型的性能指标计算对照表[3]。

其中，ρ表示车辆服务强度，Ls表示系统内乘客数的数学期望，Lq表示系统内等待服务的乘客数的数学期望，Ws表示乘客在系统内逗留时间的数学期望，Wq表示乘客在排队系统中等待时间的数学期望，λ表示单位时间平均到达的乘客数，μ表示单位时间能被服务完成的乘客数， 表示一个顾客的平均服务时间，c表示服务台个数，初值（k为常数）。表5列出出租车数量与车辆服务强度之间的关系。

图6是三种模型的比较条形图，从图所示的结果可以看出，当ρ<1时乘车效率最高，也就是说当上车点至少为6个时乘车效率最高。

3.4  问题4的解决方案

乘客目的地有远有近，为兼顾司乘双方利益，针对问题4，结合市区的实际路网情况，建立地图匹配算法中的几何算法[4]。分两个步骤：一是确定出租车轨迹点;二是用几何算法中点到线匹配，约束轨迹点与匹配点几何距离最小，以及约束匹配点与周围路段的几何形态。设匹配度指标为θ，θ越小匹配度越高，计算公式为：

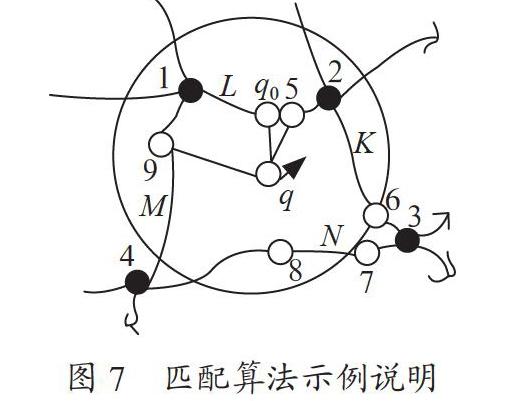
其中， 为匹配点到各路段的垂直距离，σ为匹配点行驶方向与路段方向之间的夹角，λ1、λ2为夹角和路段对匹配度的影响程度，λ1+λ2=1。地图匹配算法过程如图7所示。

在图7中，q为待匹配点，将圆心设为q的误差圆，集合路段为TY={L，M，N，K}，节点1、2和形状点5组成了路段L，节点1、4和形状点组成路段M，节点3、4和形状点7、8组成路段N，节点2、3和形状点6组成路段K，按照匹配度值的大小，L路段最终会形成轨迹点，确定轨迹点后，轨迹点到路段的具体位置将采用垂直投影法匹配，q0为修正后的位置，最终对出租车的公里数进行判断。

4  结  论

模型的优点：在处理方面数据，我们根据所给题目，详细查找了影响出租车决策的相关机理，并假设在理想状态下出租车司机的最大收益，帮助出租车司机实现利益最大化。

在问题2查找数据中，我们以咸阳机场为例，并记录总结了飞机各时段的到达高峰期，代入模型求解给出蓄车池车辆数n对司机决策的影响规律。模型图像处理采用MATLAB作图，计算了白天以及夜晚的出租车拉客选择模型，并且计算出哪些时刻和方案可以使出租车司机收益最大化，使问题结果更加可信、直观和准确。在问题3的模型建立上，采取了排队论模型的理论架构，同時简化了复杂的模型公式，尽可能用最简单的公式解决难题。

模型缺点：在问题1中，只采用了在理想状态下的数据分析，结果比较单一，没有考虑出租车排队时启动的时间，结果具有一定的误差;没有系统和全面地分析影响出租车收益的其他因素。在问题3中，由于数据过于庞大，模型求解的过程过于繁琐，降低了数据处理的灵活性。

参考文献：

[1] 黄岩，王光裕.虹桥机场T2航站楼出租车上客系统组织管理优化探讨 [J].城市道桥与防洪，2014（12）：7-9+36.

[2] 号外咸阳.咸阳机场出租车新蓄车场于6月8日投入试运行 [EB/OL].（2018-06-09）.http：//k.sina.com.cn/article_1780034803_6a192cf3027007o5b.html.

[3] 周惠暖，陈见标，刘心如，等.排队论在我国的应用学术研究综述 [J].中国储运，2020（4）：121-124.

[4] 余震，何留杰，王振飞.基于点线投影模型与几何误差制约规则的图像匹配算法 [J].电子测量与仪器学报，2018，32（4）：87-94.

作者简介：周步芳（1989—），女，汉族，甘肃白银人，助教，硕士研究生，研究方向：粗糙集、多标签学习、数学教学;付维杰（1992—），女，汉族，陕西宝鸡人，助教，硕士研究生，研究方向：图论及其应用、数学教学;乔亚琴（1992—），女，汉族，陕西榆林人，助教，硕士研究生，研究方向：机器学习、智能算法、数学教学。