圆锥曲线中距离问题的转化策略

北京四中(100034) 唐绍友

涉及距离的问题是圆锥曲线中的热点问题,常常因距离的复杂形式给学生带来沉重的心理负担,而导致运算信心不足,中途受阻,半途而废.分析其原因,主要是缺乏对距离问题的转化策略,而按部就班进行运算,陷入痛苦的运算圈子,不能自拔.基于此,非常有必要对此类问题的转化策略进行归纳和总结,给学生带来启发,旨在提高解决圆锥曲线问题的能力.

一、消元化简

从两点之间的距离公式和点线距离公式来看,涉及到的量较多,所以考虑消元化简是首要方法.如果有困难,再思考别的思路.

例1已知抛物线C:y2=4x,点M(m,0)在x轴的正半轴上,过M的直线l与C相交于A、B两点,O为坐标原点.若存在直线l使得|AM|,|OM|,|MB|成等比数列,求实数m的取值范围.

分析在距离关系：|OM|2=|MB|·|AM|中,涉及到多元与无理式的复杂代数式运算,必须进行有效的转化,才能进行正常的运算.可以考虑代入消元,再化简.

解设使得|AM|,|OM|,|MB|成等比数列的直线AB方程为x=m(m＞0)或y=k(x-m)(k̸=0),当直线AB方程为x=m时,因为|AM|,|OM|,|MB|成等比数列,所以|OM|2=|MB|·|AM|,即m2=4m,解得m=4,或m=0(舍);

当直线AB方程为y=k(x-m)时,由得k2x2-(2k2m+4)x+k2m2=0,设A,B两点坐标为A(x1,y1),B(x2,y2),则x1+x2=由m＞0,得

Δ=(2k2m+4)2-4k2·k2m2=16k2m+16＞0.

由|AM|,|OM|,|MB|成等比数列得|OM|2=|MB|·|AM|,

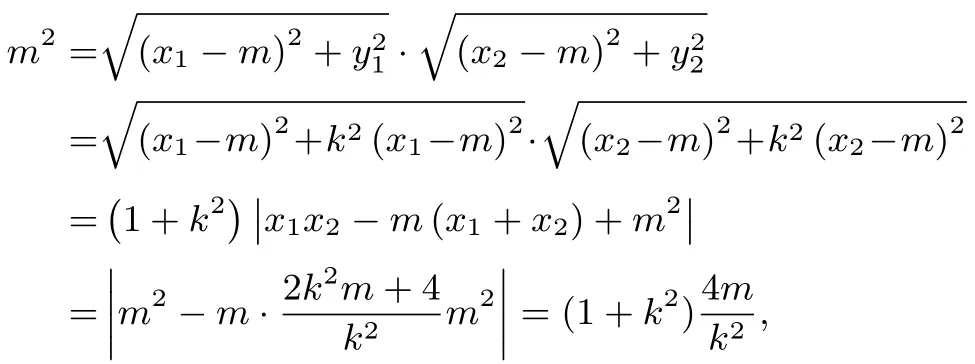
因为m＞0,所以有综上,当m≥4时,存在直线l使得|AM|,|OM|,|MB|成等比数列.

二、回归向量

因为在平面向量数量积定义中,涉及到距离,所以用平面向量数量积定义可以实现距离转化为向量的目标.比如：当向量a,b同向时,有|a||b|=a·b;由此可知例1可以用此结论求解.当向量a,b反向时,有|a||b|=-a·b;当向量a,b的夹角为θ时,有当|AB|=m|CD|(m＞0),AB//CD或AB,CD共线时,则有当距离转化为向量时,可以达到简化之功效.

例2已知点Q(2,0),过点(-1,0)的直线l交椭圆于M、N两点,△QMN的面积记为S,若对满足条件的任意直线l,不等式S≤λtan∠MQN恒成立,求λ的最小值.

分析若直接表示△QMN的面积S和tan∠MQN,计算量很大,但是用三角形面积公式和切化弦,很容易发现回归向量的线索.

解设点M,N的坐标分别是(x1,y1),(x2,y2).当直线l垂直于x轴时,x1=x2=-1,y1=-y2,所以(x1-2,-y1).所以=(x1-2)2-.当直线l不垂直于x轴时,设直线l的方程为y=k(x+1),由得(1+2k2)x2+4k2x+2k2-2=0.所以.所以

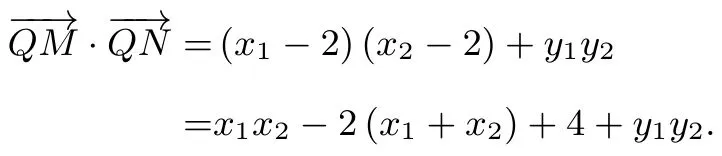
因为y1=k(x1+1),y2=k(x2+1),所以

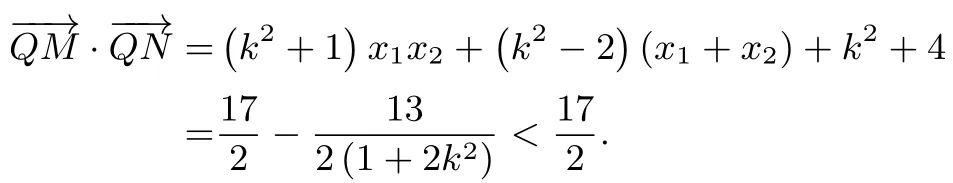
因为S≤λtan∠MQN恒成立,即恒成立.

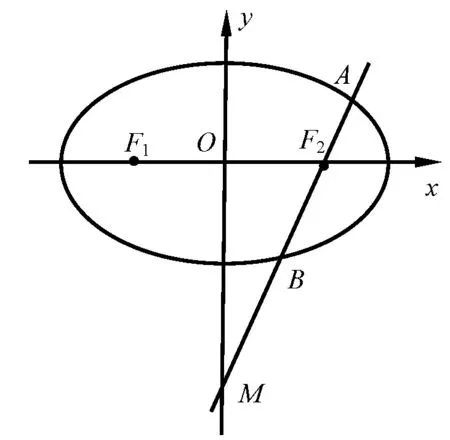
图1

例3椭圆C:=1 (a＞b＞0)的两个焦点分别为F1,F2,斜率为k的直线l过右焦点F2且与椭圆交于A、B两点,与y轴交于M点,点B在点M和F2之间,且|MB|=2|BF2|,若求离心率e的取值范围.

分析若直接用距离公式,运算量比较复杂,若利用点M、B、F2的位置关系,将距离关系|MB|=2|BF2|转化为向量关系在用坐标计算就容易了.

解设直线l:y=k(x-c),点B(x0,y0),则M(0,-kc),由|MB|=2|BF2|且点B在点M和F2之间得：因此(x0,y0+kc)=2(c-x0,-y0),从而x0=又因为点B在椭圆上,所以从而,因此分离参数得：因为所以0≤k2≤24⇒0≤

三、投影降维

涉及到共线的比例线段时,可以尝试将线段正投影到x轴或y轴上,这样可以将距离的比转化为横坐标或纵坐标的代数式,以达到降维的目的.即由二维坐标关系降为一维坐标关系,即可谓：“投影降维”.可以减少运算痛苦.

例4已知定点A(-1,1),B(1,-1),且点P是椭圆x2+3y2=4上异于A、B的动点,设直线AP和BP分别与直线x=3交于点M,N,问：是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由.

分析按常规思路,设点P(x0,y0),然后求出直线AP和BP分别与直线x=3交于点M,N的坐标,再求点P到AB、MN的距离,用三角形面积公式表示出△PAB与△PMN的面积,得到一个方程,再利用点P在椭圆上得到一个方程.联立求解可得点P的坐标.但是运算复杂.而将面积关系转化为比例线段,再向坐标轴投影,而运算特简单.

解若存在点P使得△PAB与△PMN的面积相等,设点P的坐标为(x0,y0),则因为 sin∠APB=sin∠MPN,所以所以即(3-x0)2=解得x0=因为=4,所以y0=故存在点P使得△PAB与△PMN的面积相等,此时点P的坐标为

例5过点M(0,2)斜率为k(0＜k≤1)的直线l交椭圆于H、G,点G在H、M之间,交x轴于点B,P为x轴上不同于点B的一点,Q为线段GH的中点,设△HPG的面积为S1,△BPQ面积为S2,求的取值范围.

分析求面积比,需求弦长HG与线段BQ的长,工作量较大.若能将面积比转化为HG与BQ的比,再进行投影降维,可以减少一些运算量.

解设G(x1,y1),H(x2,y2),直线l:y=kx+2.由得：(3+4k2)x2+16kx+4=0,所以

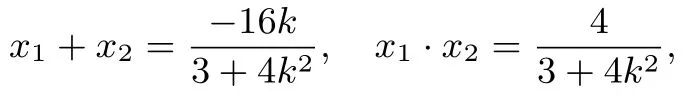
因为Δ=16(12k2-3)＞0,所以k2＞即k＞因为0＜k≤1,所以

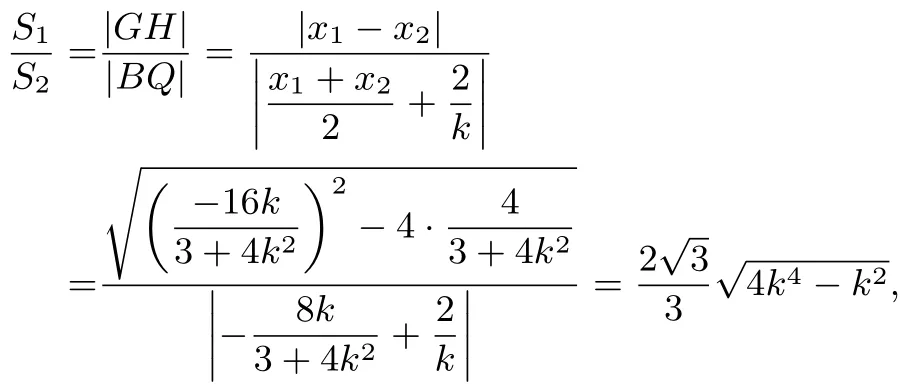
四、距离变形

距离变形主要有：(1)点线距离与两点之间距离之间的互化;(2)两距离相等化归为等腰三角形的两腰,为三线合一创造条件,为两腰所在直线的斜率互为相反数创造条件.

例6已知椭圆的一个焦点为F(2,0),且离心率为.

(Ⅰ)求椭圆方程;

(ⅠⅠ)斜率为k的直线l过点F,且与椭圆交于A,B两点,P为直线x=3上的一点,若△ABP为等边三角形,求直线l的方程.

分析直接表示等边三角形的三边长度相等,计算量大,所以先把等边三角形转化为高和边长的关系,但是计算高的运算量较大,而将高(点线距离)转化为点与垂足之间的距离(即两点间的距离),运算量大幅减少.

解(1)

(2)直线l的方程为y=k(x-2).联立方程组,消去y并整理得

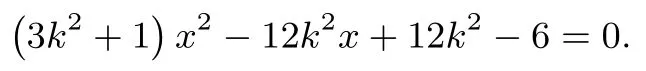
因为直线y=k(x-2)恒过定点(2,0)在椭圆内部,所以Δ＞0恒成立.设A(x1,y1),B(x2,y2).故

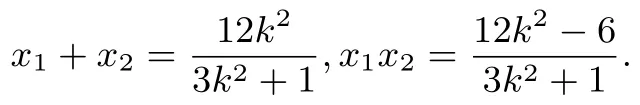
则

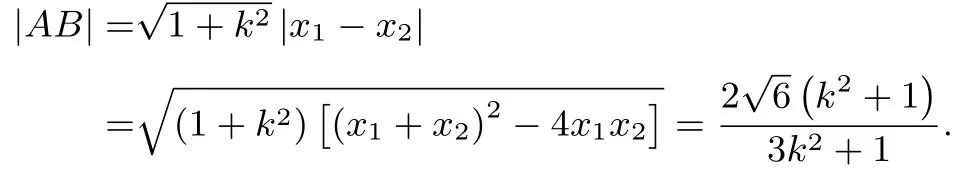
设AB的中点为M(x0,y0).可得x0==.直线MP的斜率为,又xP=3,所以

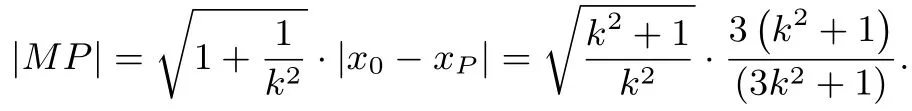
当△ABP为正三角形时,|MP|=,可得

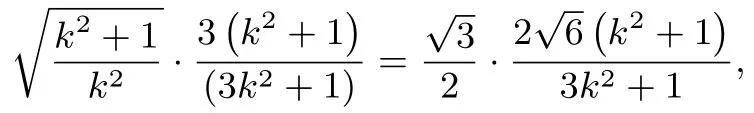
解得k=±1满足Δ＞0.即直线l的方程为x-y-2=0,或x+y-2=0.

注意计算|MP|,若用点线距离公式计算,还需算MP的方程,在求点P的坐标,可增加一倍的运算量.这里将点线距离转化为两点之间的距离是明智之举.但有时,需要将两点间的距离转化为点线距离,又可减少运算量.比如：点P在直线ax+by+2c=0上运动,且a,b,c是直角三角形的三边,其中c是斜边.求m2+n2的最小值(答案：4).将原点(0,0)和(m,n)之间距离转化为点(0,0)到直线ax+by+2c=0的距离计算挺方便.

例7(2016年朝阳一模理科)已知点和椭圆

(Ⅰ)设椭圆的两个焦点分别为F1,F2,试求△PF1F2的周长及椭圆的离心率;

(ⅠⅠ)若直线l:与椭圆C交于两个不同的点A,B,直线PA,PB与x轴分别交于M,N两点,求证：|PM|=|PN|.

分析要证：|PM|=|PN|,直接算这两个距离比较麻烦,将这两个距离转化为等腰三角形的两腰,在转化为斜率关系,再证明斜率关系,比较简单.

解(Ⅰ)△PF1F2的周长为

因为k1+k2=0,所以 ∠PMN= ∠PNM.所以|PM|=|PN|.