例谈模型在解2019年高考试题中的应用*
四川内江师范学院数学与信息科学学院(641100) 向城 刘成龙
《普通高中数学课程标准(2017年版)》提出了数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析六个核心素养.其中,数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养[1].李尚志教授指出:能够死记硬背现成公式用来解决现成模式的问题,就是数学核心素养中的“数学运算”.而能够用现成公式加以变通解决不现成的问题,就是数学核心素养中的“数学建模”.具体来讲,数学建模素养是指由数学方法构建模型解决现实问题内涵的素养.数学模型作为用数学语言表达现实问题内涵的载体,是对现实问题进行数学抽象的适用工具,是将具体的数学关系抽象出来反应特定的问题或特定的事物系统的数学关系或结构,一般以公式或者结论的形式呈现.可以看出数学模型是数学建模的核心.研究表明,数学模型具有培育创新意识、深化问题认识、减轻思维负荷、诱发问题生长、提升应用能力等教学价值.文中介绍一些数学模型在解2019年高考试题中的应用.
模型一 距离模型[2]
空间中点P(x0,y0,z0)到平面α:Ax+By+Cz+D=0的距离.
例1(2019年全国Ⅲ卷理科第23题)设x,y,z∈R,且x+y+z=1.
(Ⅰ)求 (x-1)2+(y+1)2+(z+1)2的最小值;
(ⅠⅠ)若 (x-2)2+(y-1)2+(z-a)2≥成立,证明:a≤-3或a≥-1.
解(Ⅰ)(x-1)2+(y+1)2+(z+1)2表示空间中动点P(x,y,z)到定点Q(1,-1,-1)的距离的平方,而动点P在平面x+y+z-1=0上,则由模型一得,所以|PQ|min的平方为,即(x-1)2+(y+1)2+(z+1)2的最小值为.
(ⅠⅠ)证明:(x-2)2+(y-1)2+(z-a)2≥表示空间中动点P(x,y,z)到定点Q(2,1,a)的距离的平方的最小值为,而动点P在平面x+y+z-1=0上,由模型一得|PQ|min=,即|PQ|min的平方为,所以,解得a≤-3或a≥-1,得证.
模型二 恒等式模型[3]
对平面内任意向量a和b,有a·b=.
模型三 中线长模型
△ABC的三边长分别为a,b,c.边BC,CA,AB上的中线分别记为ma,mb,mc.则有mc=.
证明如图1,在△ABD中,由余弦定理得:,同理在△ACD中,b2=amacos∠ADC,又 cos∠ADB=-cos∠ADC,所以b2+c2=.整理得:同理可得mb=
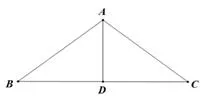
图1
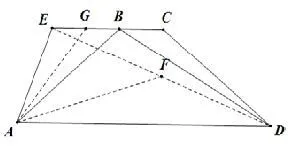
图2
例2(2019年高考天津卷理科第14题)在四边形ABCD中,AD//BC,AB=AD=5,∠BAD=30°,点E在线段CB的延长线上,且AE=BE,则=_____.
解如图2,
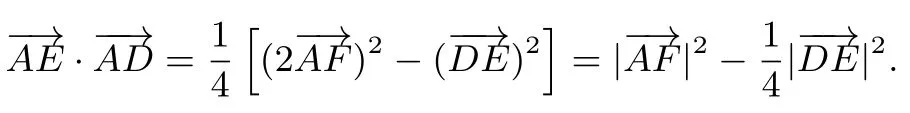
因为AD//BC,∠BAD=30°,AE=BE,所以 ∠EAB=∠EBA=30°,所以 ∠BEA=120°,在△ABE中由余弦定理易得AE=BE=2.在△ADE中由余弦定理易得由模型三得中线长AF==,所以.同理故5-6=-1.
模型四 焦点弦共线模型
设圆锥曲线C的焦点F在x轴上,过点F且斜率为k的直线交曲线C于A、B两点,直线AB的倾斜角为θ,若满足,则有.
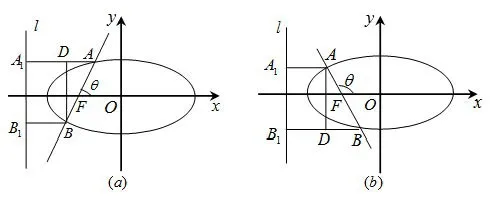
图3
证明如图3,AB过椭圆的左焦点F,左准线为l.由当直线AB的倾斜角θ为锐角时,如图3(a),显然λ>1,分别过A、B两点作AA1⊥l,BB1⊥l,垂足分别为A1,B1,过B点作BD⊥AA1,由椭圆的第二定义得,在Rt△ADB中,故;同理可得,0<λ<1时ecosθ=.(文中仅以椭圆为例.)
例3(2019年高考全国Ⅰ卷理科第10题)已知椭圆C的焦点为F1(-1,0),F2(1,0),过点F2的直线与C交于A,B两点,若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为()
解如图4,设|F2B|=m,则|AF2|=2m,|BF1|=3m.易知|BF1|+|BF2|=2a,即3m+m=2a,所以2m=a,于是|AF2|=a,所以点A为椭圆下顶点.设直线AB的倾斜角为θ,在Rt△OAF2中有cosθ=,由模型四得又因为c=1,所以a2=3,b2=2,则椭圆方程为.
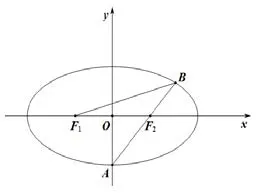
图4
模型五 三余弦模型
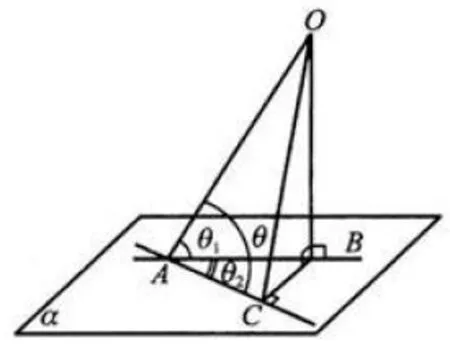
图5
如图5,A为平面a内一点,过点A的斜线AO在平面a上的投影为AB,AC为平面a内一条直线,设∠OAC=θ,∠OAB=θ1,∠BAC=θ2,则有 cosθ=cosθ1·cosθ2.
证明过点O作OB⊥AB于点B,过点B作BC⊥AC于C,连结OC,则△ABC,△OAC,△OAB都是直角三角形.则易得 cosθ=cosθ1·cosθ2.
例 4(2019年高考全国 Ⅰ卷文科第 16题)已知∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB两边AC,BC的距离均为那么P到平面ABC的距离为____.
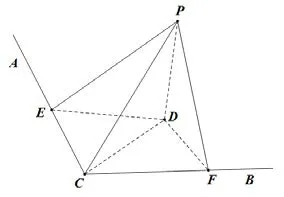
图6
解如图6,设点P在平面ABC内的投影为点D,过点P作PE⊥AC于E,PF⊥BC于F,连结CD,则PE=所以∠ECP= ∠FCP=60°,∠DCE= ∠DCF=45°,DE=DF.由模型五得 cos∠ECP=cos∠DCE·cos∠DCP,即cos60°=cos45° ·cos∠DCP,所以 ∠DCP=45°,所以即点P到平面ABC的距离为
模型六 面积模型[4]
已知平面上三点O,A,B不共线,设=则
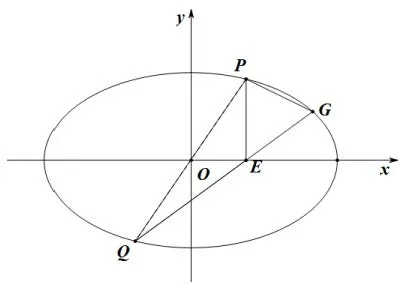
图7
例5(2019年高考全国ⅠⅠ卷理科第 21题)已知点A(-2,0),B(2,0),动点M(x,y)满足直线AM与BM的斜率之积为记M的轨迹为曲线C.
(Ⅰ)求C的方程,并说明C是什么曲线;
(ⅠⅠ)过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x轴,垂足为E,连结QE并延长交C于点G.
(i)证明:△PQG是直角三角形;
(ii)求△PQG面积的最大值.
解(Ⅰ)曲线C的方程为表示焦点在x轴上,长轴为4,短轴为的椭圆(除去左右顶点).
(ⅠⅠ)(i)略.
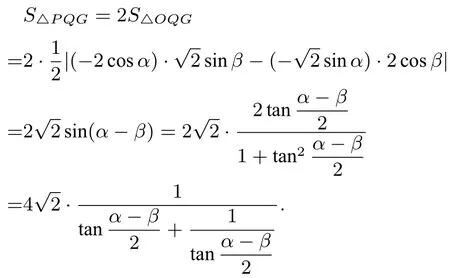
又因为
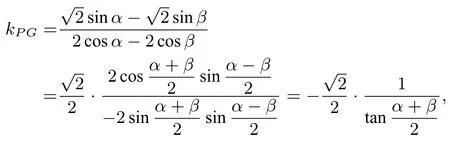
kPQ=又kPG·kPQ=-1,得所以
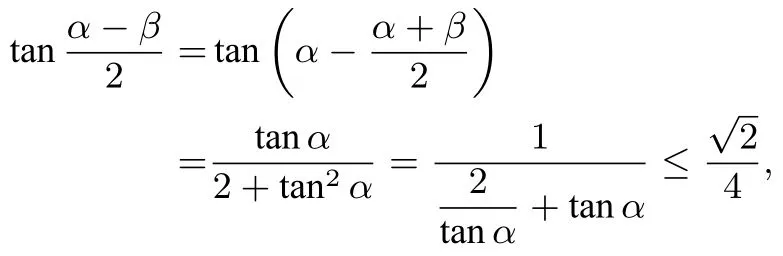
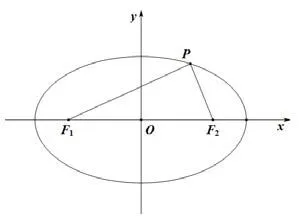
图8
模型七 焦点三角形
如图 8,若 ∠F2F1P=α,∠F1F2P=β,∠F2PF1=θ,则有离心率e==.
证明在△PF1F2中有=,易得:而所以在△PF1F2中,设∠F1PF2=θ,|PF1|=r1,|PF2|=r2,易得得r1r2cosθ=2b2-r1r2,即r1r2=所以S△PF1F2==.
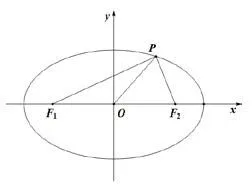
图9
例6(2019年高考全国ⅠⅠ卷文科第20题)已知F1,F2是椭圆1(a>b>0)的两个焦点,P为C上一点,O为坐标原点.
(Ⅰ)若△POF2为等边三角形,求C的离心率;
(ⅠⅠ)如果存在点P,使得PF1⊥PF2,且△F1PF2的面积等于16,求b的值和a的取值范围.
解(Ⅰ)由于△POF2为等边三角形,易得∠F2F1P=α=30°,∠F1F2P=β=60°,由模型七可得e=
(ⅠⅠ)因为PF1⊥PF2,所以 ∠F2PF1=θ=90°,由模型七可得.所以b2=16,b=4.因为存在点P,使得PF1⊥PF2,所以圆x2+y2=c2与椭圆有公共点.联立两方程得16a2-a2c2,由于a>4,故16-a2<0,所以16a2-a2c2≤0,即c2≥16,a2-16≥16,所以
从文中几个例子不难看出,数学模型是思维的支撑点,也是知识的附着点,能够将一个问题化繁为简,化难为易,化抽象为直观,化特殊为一般,更易让学生理解一个问题的本质.一个模型代表了一类问题解决的思维方式,学生掌握一个模型就相当于掌握了一类问题的解决方法.

