同心圆锥曲线中两个定值命题的证明

广东省佛山市乐从中学(528315) 林国红

一、同心圆锥曲线

定义如果两个圆锥曲线有着公共的焦点F,且与F相应的准线f也是公共的,则称这两个圆锥曲线为同心圆锥曲线.

本文讨论的是椭圆和抛物线为同心圆锥曲线的情形.

二、同心圆锥曲线的两个定值命题

命题1如图1,设椭圆和抛物线为同心圆锥曲线,F和f分别为它们的公共焦点和对应的公共准线,过抛物线上一点A作椭圆的两条切线,切点为M,N,则∠MFN为定值.

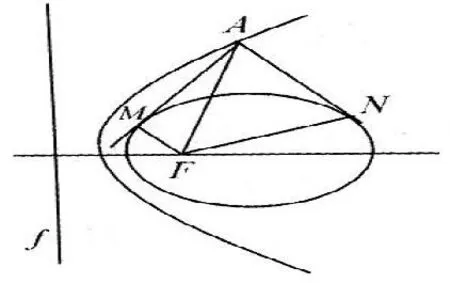
图1

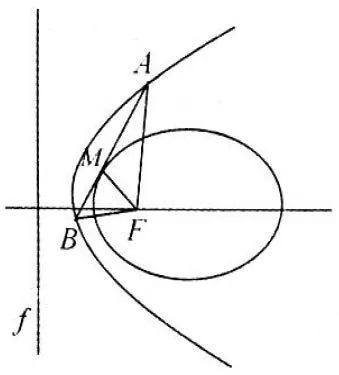
图2

命题2如图2,设椭圆和抛物线为同心圆锥曲线,F和f分别为它们的公共焦点和对应的公共准线,过椭圆上一点M作椭圆的切线,且切线交抛物线于A,B两点,则∠AFB为定值.

三、两个命题的一般证法(直角坐标证法)

(1)命题1的证明

设A(x0,y0),M(x1,y1),N(x2,y2),则直线MN的方程为联立消去y,得

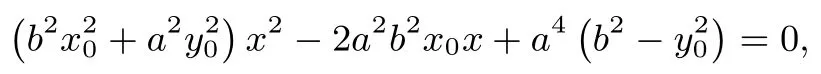
由韦达定理,有

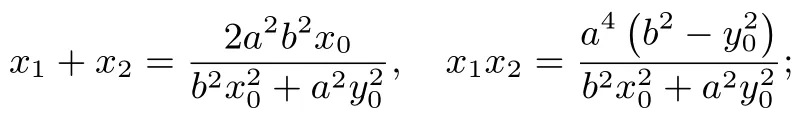
消去x,得

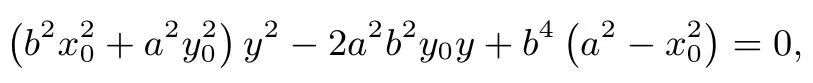
由韦达定理,有

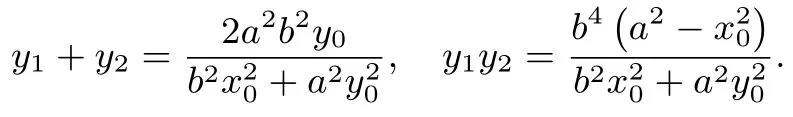
要证明∠MFN为定值⇔cos∠MFN为定值⇔cos∠MFN=为定值.

设椭圆的离心率为e,由椭圆的定义,得

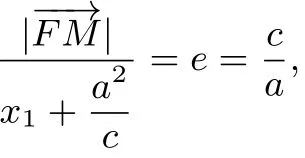
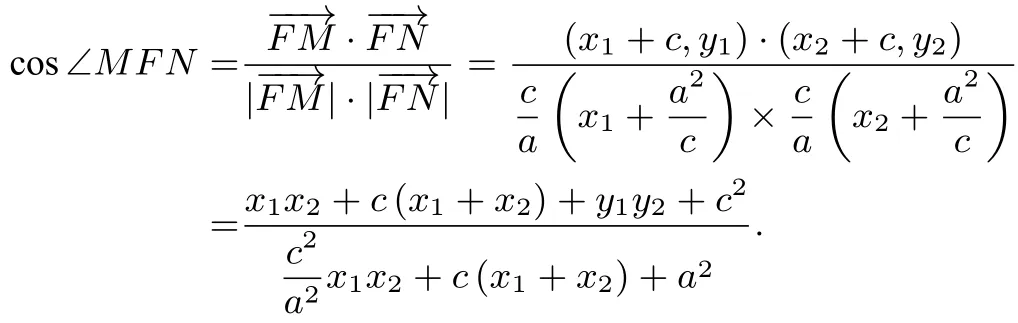
因为

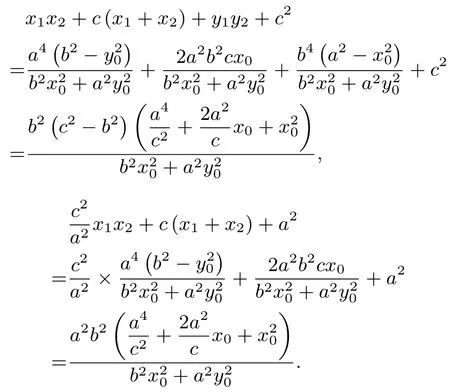
所以

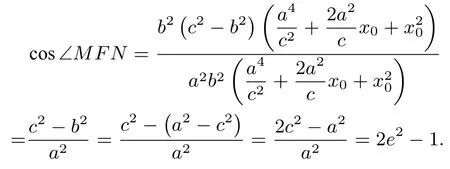
所以 cos∠MFN为定值,即 ∠MFN为定值,定值为∠MFN=arccos(2e2-1).

(2)命题2的证明

要证明∠AFB为定值⇔cos∠AFB为定值⇔cos∠AFB=为定值.其证法与命题1的证明类似,限于篇幅,不再给出证明过程.

评注上述证法的思路比较容易想到,但从证明过程可以看出,运算量很大,解答过程相对复杂,令人望而生畏;另外合理建立直角坐标系也是其中一个难点.

四、两个命题的新颖证法(极坐标证法)

先给出一个引理(如图1,以焦点F为极点,与准线f垂直的对称轴为极轴建立极坐标系)：

引理在极坐标系中,设圆锥曲线Γ的方程为ρ=则 Γ 上的点P(ρ0,θ0)处的切线方程为ρ=

引理的证明圆锥曲线Γ的方程在直角坐标系下的参数方程为

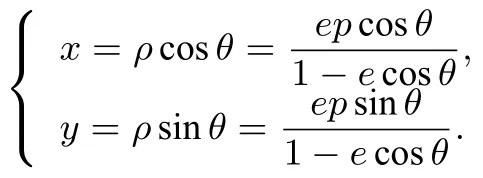
由于点P(ρ0,θ0)在圆锥曲线Γ上,故有且点P(ρ0,θ0)在直角坐标系下的坐标为 (x0,y0)=(ρ0cosθ0,ρ0sinθ0).因为

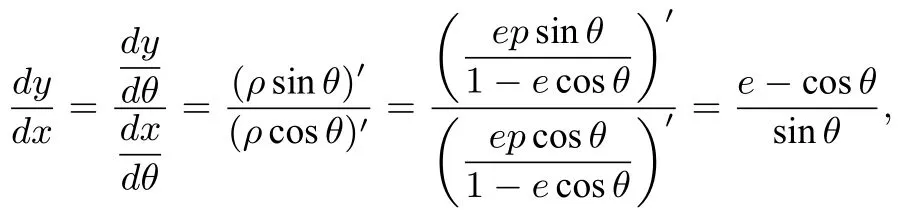
故点P(ρ0,θ0)处的切线斜率为所以,在直角坐标系下点P处的切线方程为y-y0=于是在极坐标系下点P处的切线的方程为ρsinθ-化简整理,得ρ[cos(θ0-θ)-ecosθ]=ρ0(1-ecosθ0), 又因ρ0=,故有ρ[cos(θ0-θ)-ecosθ]=ep,即ρ=所以引理得证.

(1)命题1的证明

如图1,以焦点F为极点,与准线f垂直的对称轴为极轴建立极坐标系,则椭圆方程为因为椭圆和抛物线就是同心圆锥曲线,所以抛物线的极坐标方程为.

过抛物线上一点A作椭圆的两条切线,切点为M,N,设N(ρN,θ0),M(ρM,θ0+α),其中∠MFN=α,α∈(0,π).

由引理,可得M,N两点处的切线方程分别为

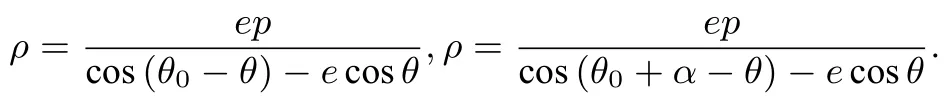
以点A的坐标为.因为点A在抛物线上,于是,化简整理,得,故α=2arccose(或由二倍角公式化为α=arccos2e2-1).所以a为定值,即∠MFN为定值.

(3)命题2的证明

如图2,以焦点F为极点,与准线f垂直的对称轴为极轴建立极坐标系,则椭圆方程为因为椭圆和抛物线就是同心圆锥曲线,所以抛物线的极坐标方程为

设椭圆上点M(ρ0,θ0),由引理,可知点M处的切线方程为ρ=与抛物线的方程联立,得化简得 cos(θ0-θ)=e,于是θ0-θ=arccose或θ-θ0=arccose,即θ=θ0-arccose或θ=θ0+arccose,于是,切线与抛物线的两个交点A,B的极角分别为θ0-arccose,θ0+arccose,故∠AFB=(θ0+arccose)-(θ0-arccose)=2arccose(或由二倍角公式化为α=arccos(2e2-1)).所以∠AFB为定值.

评注椭圆、双曲线和抛物线可以统一定义为：到定点F的距离与到定直线l(F不在f上)的距离之比为常数的点的轨迹,以焦点为极点建立极坐标系,可得到圆锥曲线的统一极坐标方程,合理地选用圆锥曲线的极坐标方程来解答相关问题时,往往能使问题的解答过程化繁为简,可起到事半功倍的效果.

对比两个命题的两种证法,极坐标证法减少了运算量,避免冗长的推理和运算过程,降低思维强度,具有直观、简捷、明快的特点,解题方法新颖独到.

五、命题的拓展

通过对上述两个命题的探究,容易得到下列两个命题：

命题3如图1,设椭圆和抛物线为同心圆锥曲线,F和f分别为它们的公共焦点和对应的公共准线,过抛物线上一点A作椭圆的两条切线,切点为M,N,则FA平分∠MFN.

命题4如图2,设椭圆和抛物线为同心圆锥曲线,F和f分别为它们的公共焦点和对应的公共准线,过椭圆上一点M作椭圆的切线,且切线交抛物线于A,B两点,则FM平分∠AFB.

命题3与命题4的证明,利用本文的引理用极坐标法很容易证明,具体的证明过程留给感兴趣的读者.

六、命题证明后的启示

问题探究的直接目的是为了寻求问题的解答,但是寻求解答却不是问题探究的唯一目的.数学解题是思维的训练,教师要多动脑筋,引导学生探研题目的一题多解,多题一解,并从中体会数学问题的探研方式与方法.使学生在掌握数学技能的同时,感受数学本质,从而积累良好的数学思维和实践经验,形成和发展数学核心素养.

数学运算是课程标准关注的核心能力,反映数学学科的基本特征,《普通高中数学课程标准(2017年版)》指出：数学运算是指在明晰运算对象的基础上,依据法则解决数学问题的素养,主要包括理解运算对象、掌握运算法则、探究运算思路、选择运算的方法、设计运算程序、求得运算结果等.而运算正是解析几何题型一项重要的考查内容,解析几何题解答过程中往往伴有较大的运算,要突破解析几何题中的繁杂运算,合理选择求解方法最为重要,选对方法,才可以简化运算,缩短解题的思维长度,提高解题效率.