“端点效应”破解不等式恒成立问题

湖北省黄石市第一中学 (邮编：435000)

1 试题呈现

(2019年新课标全国卷I文科第20题)

已知函数f(x)=2sinx-xcosx-x,f′(x)是f(x)的导函数．

(1)证明：f′(x)在区间(0,π)存在唯一零点；

(2)若x∈[0,π],f(x)≥ax,求a的取值范围．

2 试题解析与评析

2.1 试题解析：

(1)略

(2)设函数g(x)=2sinx-xcosx-(a+1)x,则g′(x)=cosx+xsinx-(a+1).

因为g(0)=0,所以一定存在x0∈(0,π],使得x∈[0,x0]时，g′(x)≥0.(若不然，即对任意x0∈(0,π],当x∈[0,x0]时，有g′(x)<0,则x∈(0,x0]时，g(x)<0,不合题意)从而有g′(0)=-a≥0,解得a≤0.

故a≤0是原不等式成立的一个必要条件．

下面证明其充分性：当a≤0时，g(x)≥0在[0,π]上恒成立．

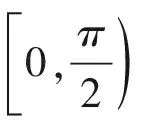
当a≤-2时，g′(x)≥0在[0,π]上恒成立，从而函数g(x)在[0,π]上单调递增，于是g(x)min≥g(0)=0,此时，g(x)≥0在[0,π]上恒成立，符合题意．

综上所述，a的取值范围是(-∞,0].

2.2 解法评析

上述解法是一种不同于官方给出的参考答案的方法，此解法由两个方面构成，一方面，通过由给定区间左端点的导函数值建立不等式g′(0)≥0,求得a的范围，此范围是原不等式恒成立的必要条件；另一方面，证明在此范围内原不等式恒成立，即是原不等式恒成立的充分条件．由这两个方面知，所求范围为原不等式恒成立的充要条件，故而正确．

不等式恒成立求参数取值范围，是高中数学常见问题，也是高考的热点．解决此类问题的通法是构造函数，对参数分类讨论；也可以优先采用分离参数法．然而并非所有的问题都能奏效，例如此题就不是很好解决，但倘若能考虑区间端点的性质，若区间端点处的函数值为零，可先找到一个不等式成立的必要条件，从而缩小范围，然后再证明必要条件也是充分条件，那么即可求得结论．

3 解法引申与探究

3.1 端点效应

在适当考虑区间端点的性质，先找到一个不等式成立的必要条件，从而缩小范围，然后再证明必要条件也是充分条件，那么即可求得结论．这种必要性探路，再证充分性分方法，我们称之为“端点效应”．它实质上是从求“不等式恒成立”的必要条件入手，求得参数的范围，再证明其为充分条件．

3.2 解法原理

设函数f(x)中含参数m,集合A是给定数集，且∀m∈A,f(x)>0恒成立的m的取值范围为集合B．若∃x0∈A,由f(x0)>0解得m∈C(此时B⊆C)；且当m∈C时，f(x)>0恒成立，则B=C.

在审题中注意研究给定区间左右端点的函数值或导函数值，依据恒成立的不等式(或其变形)，建立一个必然成立的不等式，解此不等式得到参数的一个范围(必要条件)；然后再证明该范围(或该范围内的一部分)是“不等式恒成立”的充分条件．以上两个方面，即确定了参数的取值范围．

3.3 适用类型

①不便于参变分离；

②参变分离后的函数形式比较复杂．

3.4 解题步骤

①移项，将所有变量移到一边，使不等式右侧为0；

②计算端点处函数值，验证端点处函数值是否为0，若为0，则可继续往下走，否则此题不适合使用端点分析法．

具体操作如下：

(1)必要性条件缩小范围

①若f(x,m)≥0(m为参数)在[a,b](a,b为常数)上恒成立，且f(a)=0(或f(b)=0)，则f′(a)≥0(或f′(b)≥0)．此法应用于区间端点的函数值为零的情况．

(2)证明充分性得结果

求f′(x)并判断f(x)的单调性，然后表示f(x)的最小值f(x)min,使得f(x)min≥0即可．注意第二步一定要利用第一步中参数的范围．

4 应用举例

4.1 区间端点的函数值为零型

例1(2017年新课标全国卷II文科第21题改编)已知函数f(x)=(1-x2)ex,当x≥0时，f(x)≤ax+1,求a的取值范围．

解析设函数g(x)=(1-x2)ex-ax-1,则g′(x)=(-x2-2x+1)ex-a.

因为g(0)=0,所以g′(0)=1-a≤0,即a≥1.

故a≥1是原不等式成立的一个必要条件．

下面证明其充分性：当a≥1时，由g′(x)=(-x2-2x+1)ex-a,可得g″(x)=(-x2-4x-1)ex<0(x≥0),所以函数g′(x)在[0,+∞)上单调递减，此时，g′(x)≤g′(0)<0,于是函数g(x)在[0,+∞)上单调递减，因此g(x)≤g(0)=0,符合题意．

综上所述，a的取值范围是[1,+∞).

评注本题由给定区间左端点的函数值为0，得到一个关于其导函数的不等式g′(0)≤0,得a的范围，成为原不等式恒成立的必要条件，然后再证明此范围是原不等式恒成立的充分条件．

例2(2016年新课标全国卷II文科第21题改编)已知函数f(x)=(x+1)lnx-a(x-1),当x∈(1,+∞)时，f(x)>0,求a的取值范围.

解析由f(1)=0,要使得当x∈(1,+∞)时，f(x)>0,则必有f′(1)≥0.

故a≤2是原不等式成立的一个必要条件．

综上所述，a的取值范围是(-∞,2].

评注本题由给定区间左端点的函数值为0，得到一个关于其导函数的不等式f′(1)≥0,求得a的范围，成为原不等式恒成立的必要条件，然后再证明此范围是原不等式恒成立的充分条件．

4.2 区间端点的函数值与导数值均为零型

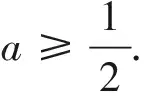
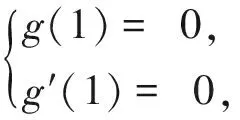
例4(2018年湖北省部分重点中学高三期中联考第21题改编)已知函数f(x)=2x-ln(2x+1),g(x)=ex-x-1,当x>0时，kf(x)≤g(x)恒成立，求实数k的范围．

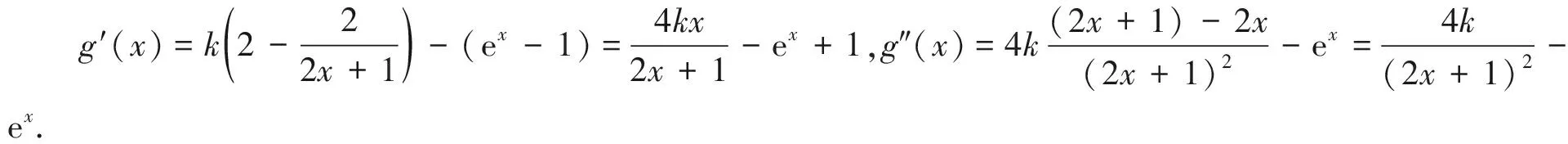
5 问题总结

由上可见，对含参不等式恒成立问题，端点效应法是一个不错的方法，现总结如下：

对于不等式f(x,m)≥0(m为参数)在[a,b](a、b为常数)上恒成立，求m的取值范围的问题，可按如下处理 (其中m为参数，a、b为常数)：

(1)若f(a,m)=0,则由f′(a,m)≥0 (一阶导含参数)得到必要条件，再证明必要条件是充分条件；

(2)若f(b,m)=0,则由f′(b,m)≤0 (一阶导含参数)得到必要条件，再证明必要条件是充分条件；

(3)若端点处的一阶导数值也为0，则可求二阶导数，代人端点值，继续按(1)或(2)执行，得到必要条件，再证明必要条件是充分条件．

“端点效应”是一种必要性探路，再证充分性的方法，虽然它求出的参数并不一定就是所求的实际范围，但是可以限定问题成立的大前提，缩小参数的讨论范围，在一定程度可以减少分类讨论的类别，降低了思维的成本．