例谈几何画板辅助课堂教学

安徽省六安市金安区毛坦厂学校 (邮编：237182)

几何画板作为一个经典的数学教学软件，对培养学生的直观想象能力可以发挥重要作用.它不仅能根据几何对象间的关系，精准地画出几何图形，还可以轻易地进行几何变换和迭代，对几何图形的数量属性作出度量.动画功能可以从运动的观点研究问题、直观地展示几何性质和规律.多样的显示功能提高了使用几何画板进行数学教学的效果.笔者通过实际的例子，探讨在初中数学教学的各个环节中，如何在恰当的时机，灵活方便地使用几何画板，来增进学生的兴趣、加深学生的理解和掌握、发展学生的探究能力和创新意识、从而提高学生对几何图形的直观想象能力素养.

1 新知探究中

在新授课中，根据教学需要可以利用几何画板辅助探究，或启发思路，或直观显示结论.

1.1 直观演示显本质

例1二次函数各参数对图象形态、位置的影响.

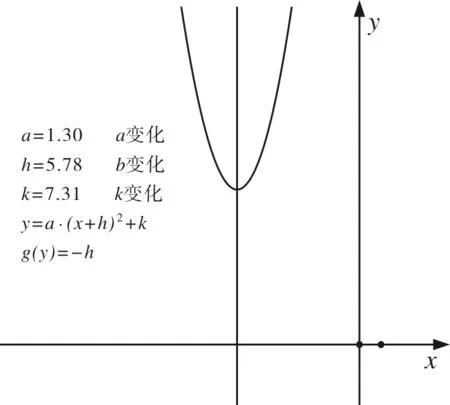
图1

二次函数顶点式y=a(x+h)2+k中，a决定开口，h决定对称轴，k决定顶点纵坐标.在几何画板中，可以生成参数a、h、k可变的y=a(x+h)2+k图象，展示当a、h、k分别变化时，对图象分别有什么影响.相比于传统的板书作图，更直观展示了各参数的几何意义.

1.2 验证激发证明

例2 证明平行线性质前，先行验证.

作出平行线a、b后，用第三条直线c去截，度量出截得的∠1、∠2、∠3、∠4.移动点A、B以改变直线c,但内错角、同位角、同旁内角的数量关系始终保持不变.利用几何画板，先验证结论恒成立，可以激发学生寻找证明过程的兴趣，为下一步的证明创造积极的动机，促进对思路的寻求.

例3 勾股定理逆定理，模拟尺规作图验证.

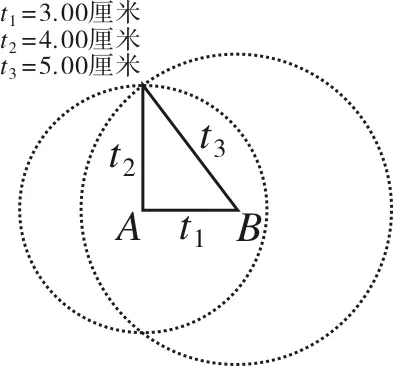
图3

遵照课标精神，初中教材通常对勾股定理逆定理不予证明，仅用一组勾股数为三边，手工作出对应三角形作为验证.这会显得论证不够充分(没有演绎推理)，而且由于举例太少(因为画图不便)，也显示不出来归纳推理.利用几何画板，先以t1为长度作线段AB,再分别以A、B为圆心，t2、t3为半径作圆，两圆交点为三角形第三个顶点.输入t1、t2、t3的不同取值，立得相应三角形.当t1、t2、t3为勾股数时，能构成Rt△,当t1、t2、t3不是勾股数时，能构成一般三角形或不能构成三角形.这里的思路同手工作图，但却相当节省画图时间.可以与手工作图相配合，帮助学生增加对勾股定理逆定理的熟悉程度和直观感受，同时也能进一步加深对三角形三边所需条件及三边和三角形形状之间关系的理解，为高中进一步学习三角形边角关系打下直观基础.

又如，反比例函数k的几何意义.

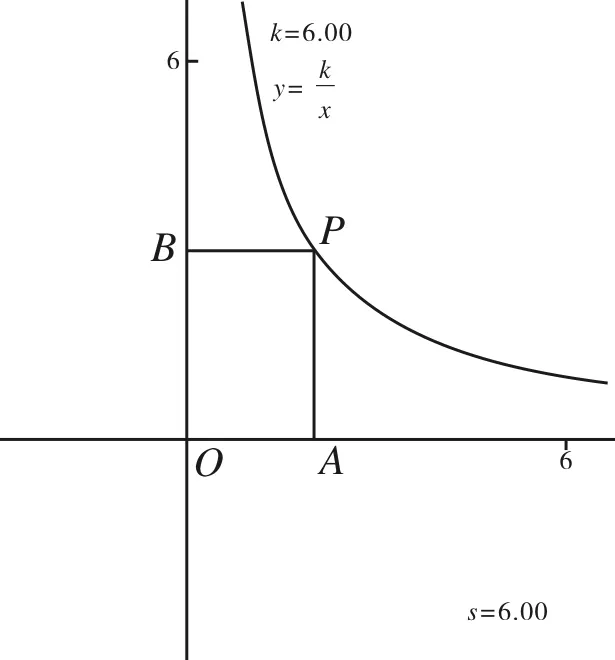
图4

在学习完反比例函数概念和位置、增减性之后，学习k的几何性质时，如果先说“在双曲线上任取一点P,分别向x轴和y轴作垂线段，垂足为A、B,垂线与坐标轴围成的矩形，请观察其面积有什么特点”，接着拖动点P，学生能够看到，虽然矩形形状改变了，但面积始终保持不变.再引导学生观察出面积和k的关系.学生会惊讶发现这个变动中的不变，教师再问一句“为什么？”学生将马上陷入对“眼见为实”背后原理的探究中，如此得来的知识将非常牢固.这种移动点P的操作，是不借助计算机无法展示的，是传统教学技术达不到的.

2.拓展探索中

2.1 画纸笔不可画，动纸笔不可动

例4 平面镶嵌问题.

平面镶嵌是数学基本问题.在初中数学四边形内容学习后，可以做一些简单研究，拓宽学生的数学思维.把问题限制在正多边形镶嵌上之后，利用正多边形内角拼成周角，可以解方程求出多种不同组合下的镶嵌[1].再利用几何画板展示不同组合，让方程解出的“数”转变为切实可见的“形”，使学生体会数与形的联系，同时感受数学美.

这种复杂的图形，是手工作图无法快速展示的.但是利用几何画板的平移、旋转、反射等变换及迭代功能，却可以较快地准确实现.

正三角形和正方形镶嵌的情形：

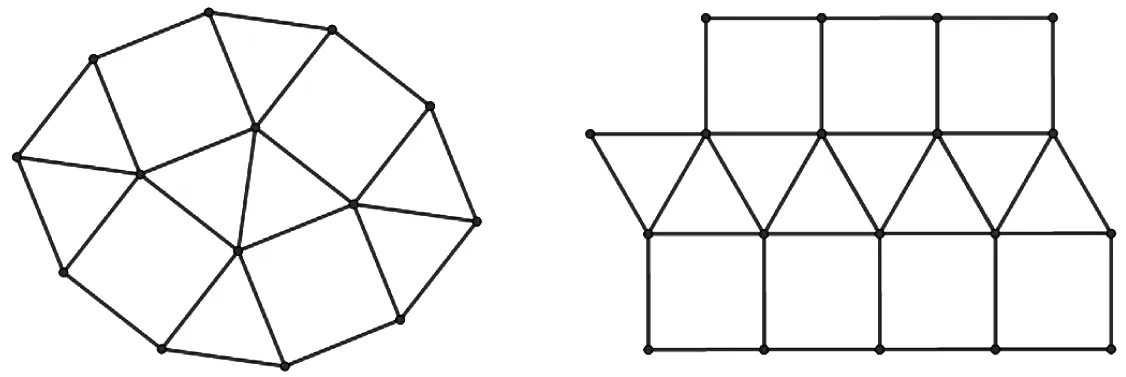
正方形和正八边形镶嵌的情形：

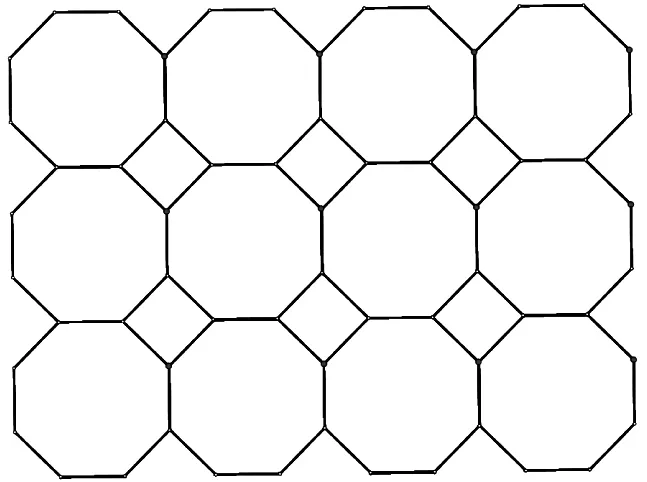
任意四边形可平面镶嵌的情形：

图5

由于四边形内角和360°,所以任意四边形的四个内角总可以拼成周角，因此通过旋转、平移等变换，可以构造出任意四边形平面镶嵌的图案.随意拉动图中四边形的顶点，就可以改变四边形的形状，以至整个图案形状的改变.无论四边形的形状如何，但这种平铺方式始终能完整地镶嵌成平面.利用几何画板图形的动态性作出的超出学生想象的展示，使学生产生了很强的新鲜感，学习数学的兴趣变得更加浓郁.

例5 两次轴对称变换可得平移变换和旋转变换.

对一个图形进行连续两次轴对称变换，当对称轴相交时，相当于一个旋转变换，旋转角是对称轴夹角的2倍，当对称轴平行时，相当于一个平移变换，平移距离是对称轴距离的2倍[1].对称轴位置可以改变，图形的形状也可以改变，直观展示了三个几何变换之间的内在联系.将孤立知识点间的内在联系显示出来，会为同学们打开一个新天地，帮助他们强化用联系的观点看问题，像孙维刚所说的“八方联系，浑然一体”整体结构教学观所提倡的一样.并且也利于学生以后学习线性代数中的变换，打下一个感性基础.这种对所学知识的进一步探究虽然只是一个苗头，但能让学生意识到，课标知识点下有着鲜活广阔的学术世界，使他们接受到知识美的感染.

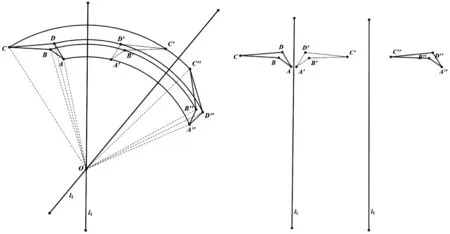
图6 图7

2.2 变化之中有不变，奇妙性质蕴其间

例6 四边形中点四边形的性质.

四边形是除三角形外，初中研究最详细的多边形.各种不同四边形间概念的区别与联系，以及它们的性质、判定、相关推理及习题，能很好地培养初中生的演绎推理能力和概念思维能力.其中有个很特别的性质，即四边形的中点四边形的形状问题.任意四边形的中点四边形，都是平行四边形；任意矩形的中点四边形是菱形；任意菱形的中点四边形是矩形；任意正方形的中点四边形是正方形.形中有形，形形相依，规律非常有趣，常作为训练学生综合运用各特殊四边形性质与判定的习题.但教师若用多题归一的眼光来引导学生审视，为何有这些性质？本质是什么？深入挖掘，则会发现：由三角形中位线定理，HG与EF均平行且相等于AC,EH与FG均平行且相等于BD.因此，若AC=BD,则EFGH为菱形；若AC⊥BD,则EFGH为矩形；若AC=BD且AC⊥BD,则EFGH为正方形.原来，中点四边形的形状由其各边是否平行和相等来决定，而这又由原四边形的两条对角线来决定.所以，筝形的中点四边形也是矩形，任意对角线相等的四边形的中点四边形都是菱形.经过这种对习题的挖掘与综合，学生将潜移默化出一种探究思维，不知不觉提高数学上的创造力和研究力，在变幻多端的具体数学问题中，抽丝剥茧找到问题本质，提高数学的抽象思维能力.

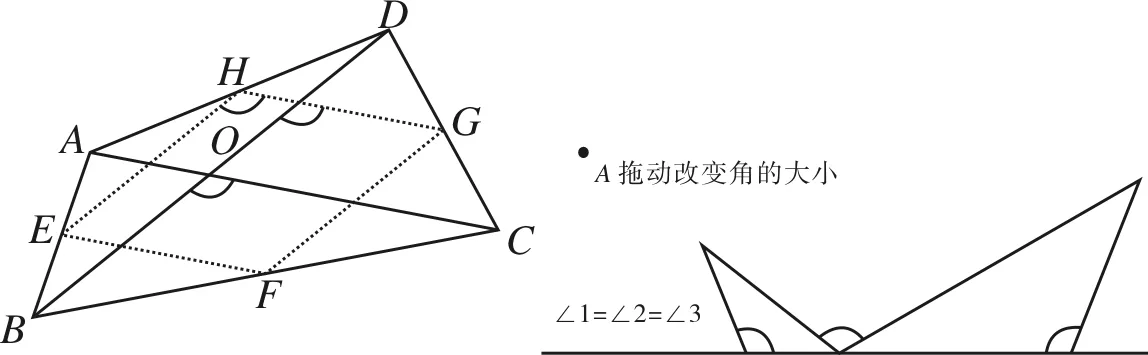
图8 图9

例7 一线三等角问题.

一线三等角是平面几何证明中常见的基本模型，一线三直角是其特例.如何在变化中展示不变的性质，几何画板带来了极大方便.拖动图中点A,可将∠1=∠2=∠3的大小改变为任意角度(<180°),但两三角形相似(特例是全等)却始终保持不变.这是手工作图无法充分直观展示的.

3 习题研究中

3.1 动点动图与函数，一目了然在心中

例8 点P在矩形ABCD上沿B-C-D-A上运动，△ABP面积关于点P运动路程的图象.

如图10，动点动图形问题，用几何画板动态展示最为合适.相比于传统的分段分析，更能直观显示点和图形运动的实际情况.点P开始运动时，还能在函数图象上看到对应于该时刻的点.清晰地显示了分段函数各段上的情形以及分界点时的情况.

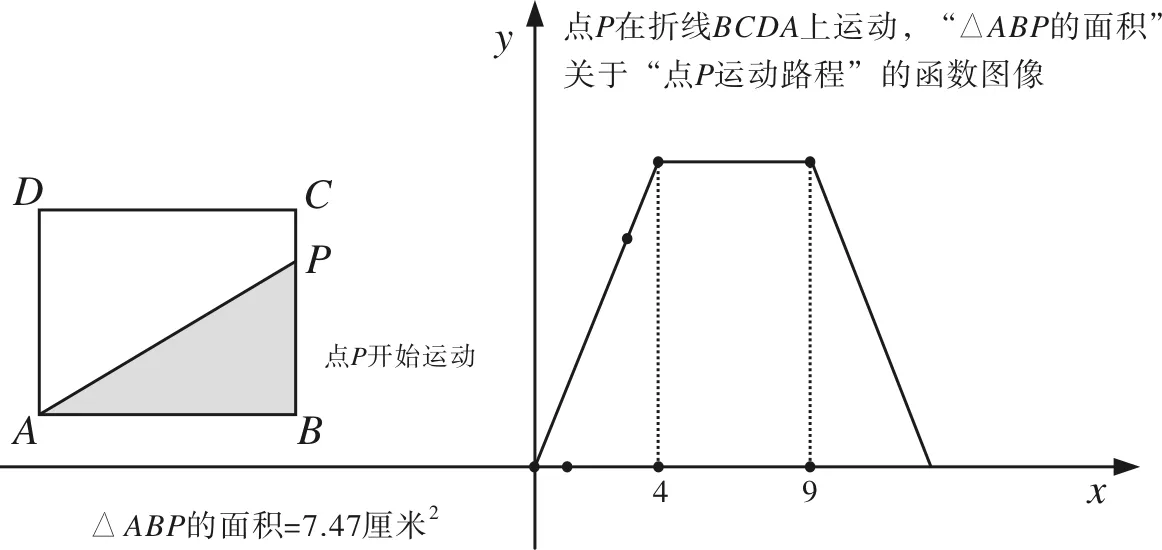
图10

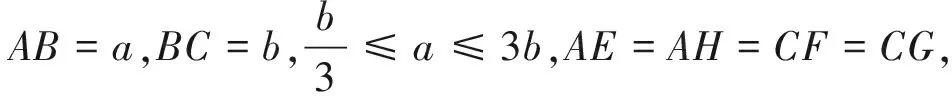
对这类问题借助几何画板处理，有助于学生直观把握函数概念中“一个量变化，另一个量也随着变化……对于x在允许取值范围内的每一个值，y都有唯一确定的值与之对应”，加深对函数和函数图象概念的理解.按照马克思的观点，“有了变数，运动进入了数学，辩证法进入了数学”.这种几何画板展示让学生看到，很多复杂的问题中都蕴含着函数关系，因此，很能够提高学生用运动和辩证的观点去看待现实世界中的数量关系，对提高数学素养有很高的价值.

图11

3.2 复杂图形精确画，一网打尽所有解

例10 正方形ABCD边长为6，动点M、N满足AM=BN,求线段CF的最小值.

图12 图13

易证△ADM≌△BCN,故∠3=∠2,又易由对称性知∠1=∠2,故∠1=∠3.而∠1+∠FDA=90°,从而∠3+∠FDA=90°,因此∠DFA=90°,点F轨迹是以DA为直径的半圆.在展示此题的逻辑推理解法之后，用几何画板精确画图，并拖动点M,让学生亲眼所见点F轨迹恒在隐形圆上，不可谓不是一种美的享受.

例11 如图13，长方形ABCD中，BC=8,AB=6,沿AE折叠，点B与点F重合.有点P在矩形CDFE中，且△AEP和△ECP均为Rt△,求△PCD面积.

本题应从两个直角三角形入手，分析点P应在的轨迹.要使△AEP为Rt△,则点P应在图中大半圆轨迹上，要使△ECP为Rt△,则点P应在图中小半圆轨迹上，因此点P应在两半圆交点P1和P2处.接着再寻找相似等关系解题.相比于手工作图，几何画板展示该题，可以更加精确、快捷、清晰.常规讲题方法与借助几何画板演示相结合，可以在习题教学中提升教学效果.

3.3 任你风吹雨打，定值巍然不动

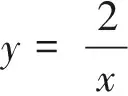
图14 图15

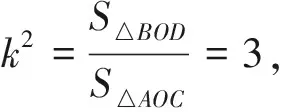
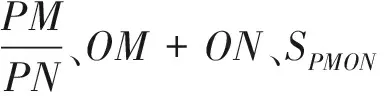
图16 图17

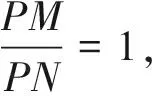
运动的问题用几何画板运动地展示，能突破纸笔教学的局限.变化的图形中却有定值，使用几何画板动态展示变化中的这种不变，能激起学生对物质世界规律的相似认识：即使自然界斗转星移，沧海桑田，变化万端，但总有一些客观规律隐藏在其中.坚持寻找这些规律，就是宝贵的科学精神.

4 数学文化与兴趣激发

4.1 迭代生成繁复图，抽象可达艺术景

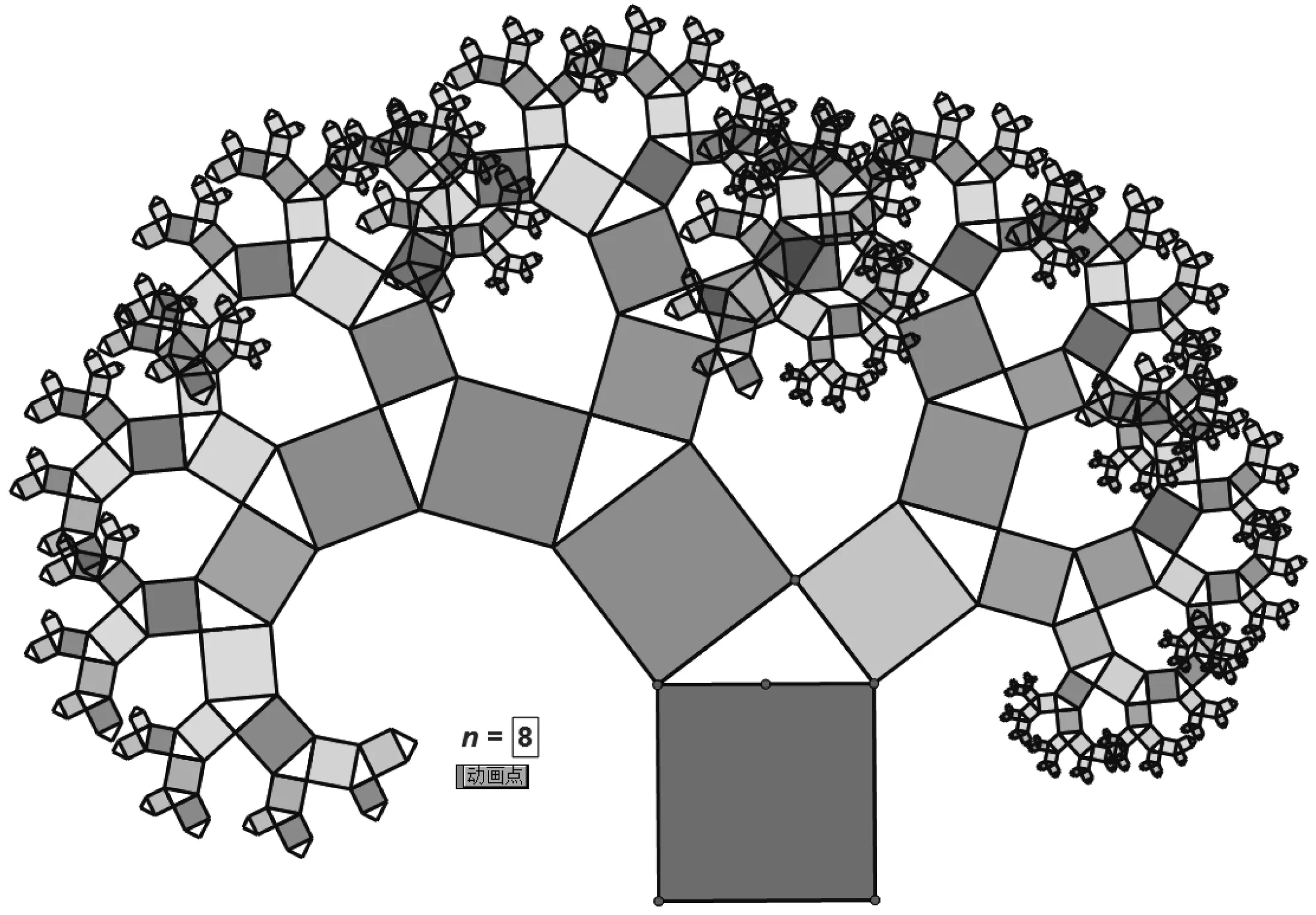
图18

几何画板的迭代功能，可以将多次重复的事情交给计算机去做，因此容易创造出大量有用的图形.通过该功能，也能作出分形图等美丽的图像.勾股树是一个方便易作的例子，可以很快制作出来，加强学生对几何世界和数学世界的兴趣.直角三角形三边上的正方形，是勾股树中的基本图形，可用参数控制迭代深度，用动画使树摇动，用参数颜色使树多彩.

4.2 函数公式有声音，物理机器与数理

自古至今，音乐始终就与数学之间有密切的联系[2].声音信号可以通过傅里叶级数转化为周期正弦信号的叠加.同学们初学函数，只知道解析式、图像、计算，如果这时告诉他们，函数还有声音，不同的函数还有不同的声音，而且声音还可以通过函数图像直观看到“波形”，这对孩子们的震撼无疑是非常大的.而且增加了学生们对数学与物理学等自然科学之间联系的了解，也进一步体会了计算机等现代科技的魅力，有助于提高对知识整体的求知欲.

利用几何画板，可以对函数解析式生成“声音”操作按钮.如y=cos(30xπ)+tan(65xπ+20)+sin(3x2+5xe+50)·sin(1.0472+x6-9x+50)能发出充满科技感的声音，y=10sin(2π·512x·sgn(ln(sin(2.6πx))))能发出电话忙音，y=sin(cos(tan(ex)))能发出发动机的声音.为什么如此呢？这从函数图像上可以看出来.例如y=sin(cos(tan(ex)))的图像充满间断与变化，有类似于周期性的特点，而y=10sin(2π·512x·sgn(ln(sin(2.6πx))))的图像则更加有规律，而y=cos(30xπ)+tan(65xπ+20)+sin(3x2+5xe+50)·sin(1.0472弧度+x6-9x+50)的图象则含有更多随机性.接着我们再听听一次函数、二次函数的声音，则只是很轻的一声“啪”而已，这则是由于其函数图象过于单调和简单.由此，学生们不仅感觉打开了新世界的大门，而且能体会到初中数学的基础性作用，增加信心和学习动机.

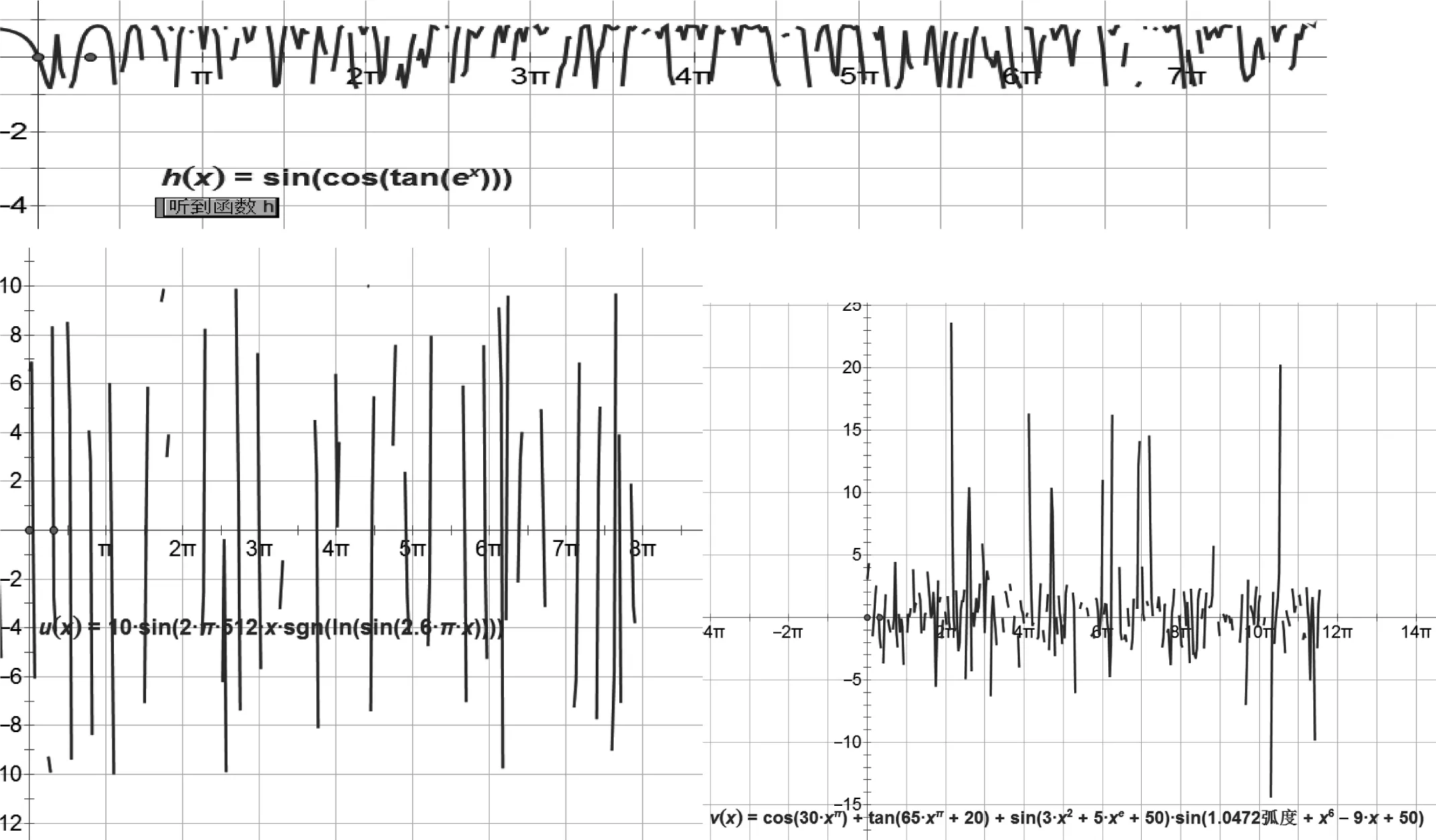
图19

5 结语

几何画板不仅可以作为教师教学的辅助工具，也可以作为学生数学兴趣小组学习的内容，教师应加强对几何画板的学习，并在教学的各个环节合理使用.根据义务教育新课程标准以及教育信息化发展规划等国家文件的要求，教师应积极主动亲近教育信息技术、更新思想观念、改进教学方式，将信息化手段与学科教学有机结合起来，利用信息化手段补充传统教学之不足，培养更全面更高素质的现代化建设人才.