一种内置式永磁同步电机死区补偿方法的研究

朱明祥，孙红艳

(南京师范大学泰州学院 电力工程学院，江苏 泰州 225300)

0 引 言

内置式永磁同步电机(Interior Permanent Magnet Synchronous Motor, IPMSM)具有功率密度高、效率高、调速范围宽等优点，广泛应用于电动汽车电驱动系统中。其中空间矢量脉宽(SVPWM)技术具有电压利用率高、谐波分量小以及易于数字化实现等优点，在电动汽车IPMSM电驱动系统的电压型逆变器中具有广泛的应用。在SVPWM方案的逆变器驱动系统中，由于理想的开关特性无法实现，为了防止上下桥臂同时导通造成短路故障，需要在上下桥臂的驱动信号中加入死区时间以防止短路现象的发生。而死区时间地引入，会使得逆变器输出电压的基波分量减小、谐波分量增加，并引起零电流钳位效应，进而使输出电流、输出转矩发生严重的畸变和脉动，这一现象在低速时尤为明显。

为了解决由于死区效应造成的不良影响，国内外学者提出了多种死区补偿算法。文献[1]和文献[2]在传统矢量控制算法的基础上，增加神经网络谐波电流环实现电流谐波的分解和提取，并将所提取的电流谐波通过神经网络训练获得补偿电压进行死区效应补偿，但该算法对控制器性能要求较高。文献[3]研究了逆变器死区时间的设置及其对电压矢量的误差影响，并设计相应的补偿算法，验证了该算法的有效性，但该方法中电流极性未进行准确判断。文献[4]分析了因死区时间、功率器件导通关断时间引起的误差电压矢量，并提出一种改进型电压前馈死区补偿算法，利用电流环计算好的电流矢量幅值分量的线性组合实现对定子电压 的补偿，该算法能有效地改善输出电流的波形并消除了零电流钳位现象。文献[5]提出采用Kalman滤波算法估计扰动电压来抑制由于αβ坐标系的5次与7次电流以及dq坐标系下的6次谐波电流所引起的电压畸变、转矩脉动以及算法效率的降低。文献[6]提出一种RRC策略减小电流谐波和畸变率，并将该电流应用于死区补偿中，取得了较好地补偿效果。文献[7]采用自适应参数独立的策略进行补偿电压的计算，并利用观测器对扰动电压进行观测与抑制。

在利用电流极性对死区效应进行补偿时，电流趋近于零所产生的零电流钳位现象以及高次谐波，造成电流极性检测存在很大困难。通常做法是将采样电流进行低通滤波，之后再进行极性检测以及死区补偿，但低通滤波造成的相位延时在实时控制中需要尽量避免。因此本文提出一种基于ADALINE陷波器的死区电压补偿方法，通过ADALINE算法滤除直轴与交轴中存在的6次和12次谐波以增强死区补偿算法的可靠性。并通过仿真与试验验证了所提方法的正确性与有效性。

1 死区效应与补偿

1.1 死区效应

如图1所示，以一相桥臂的VSI进行说明。正负载电流以从左向右指向负载的箭头表示。从图1中可以看出，加入死区时间后，在T1和T4都处于关断期间，电流通过续流二极管D1和D4续流。若电流为正，则通过D4续流，死区时间A相的端电压为0；若电流为负，则通过D1续流，死区时间内A相的端电压为vdc。

图1 逆变器的单相桥臂

图2 考虑死区时间、开关延时以及压降的理想实际电压波形

图2中a区域为上下桥臂导通关断时的理想控制电压信号；b区域为a区域基础上加入死区时间后的波形，但实际中因为存在开关管与二极管压降、开关管导通关断时间等非线性因素，使得控制电压漂移非常严重。考虑这些非线性因素后，器件的控制电压波形如c区域和d区域所示[8-11]。将图中i>0表示为i+，i<0表示为i-，则相应的电压增益与损失可以推导为：

(1)

(2)

式中,vdc，vsw，vd分别为直流母线电压，晶体管和二极管导通压降；tr，tf，Ton，Toff，TPWM分别为开通和关断延时时间，高低电平持续时间和开关周期。

为将上式进行简化，做如下处理：

Tdead=(Td+Tr-Tf)

(3)

vsw=vd+Δv0

(4)

式中，Δv0为二极管与开关管的导通压降差值。因此，式(1)和式(2)可以变换为

(5)

(6)

对于B、C相，其原理基本相同。为了进一步简化式(5)和式(6)，以图2电流方向为判别依据，则死区的增益或损失电压可以表示为

(7)

1.2 死区补偿

通过以上分析，在IPMSM的三相电流中，可以划分出6种可能性，如表1所示。而此种方法需要对电流矢量角度进行实时计算，进而判别出在何扇区。实际运行中存在计算量庞大、实时性要求高以及编程困难等缺点，因此不利于进行死区补偿。为此，通过iα和iβ的线性组合判断电流所在的扇区，进而实现电压补偿[4]。

(8)

规定a、b、c大于0时取1，a、b、c小于0时取0，令N=4c+2b+a,则可以得出表2。

在实际应用中，还需对采样之后的电流进行适当的滤波才能进行矢量变换的控制，否则由于死区效应造成的高次谐波会影响补偿效果，为此采用ADALINE陷波器对直轴和交轴电流中的高次谐波进行滤除，进而可以获得更加理性的效果。

表1 电流矢量角和补偿电压关系表

表2 a, b, c和补偿电压关系表

2 控制器设计

假设IPMSM的电感为常数，忽略电阻随温度变化所发生的改变，以定子电流与定子电压为状态变量，构建出dq坐标系下的IPMSM数学模型[12-14]：

(9)

式中，p为微分算子；Ld和Lq为d轴和q轴电感；ud、uq、id、iq分别为d轴、q轴电压和d轴、q轴电流；Rs为定子电阻；ψf为永磁体磁链；ωe为电机的电角速度。

在dq坐标系下，电流谐波的主要阶次为6次和12次，直轴与交轴的电流表达式可以写为[15-16]

(10)

式中，ωd0为直轴电流的直流分量幅值；ωd6_1和ωd6_2分别为6次谐波的余弦分量幅值和正弦分量幅值；ωd12_1和ωd12_2分别为12次谐波的余弦分量幅值和正弦分量幅值；ωq0为交轴电流的直流分量幅值；ωq6_1和ωq6_2分别为6次谐波的余弦分量幅值和正弦分量幅值；ωq12_1和ωq12_2分别为12次谐波的余弦分量幅值和正弦分量幅值。

为此，设计出基于ADALINE的陷波器，将6次、12次谐波滤除后再进行死区补偿。ADALINE的结构如图3所示，此处以直轴电流为例，交轴电流的陷波方式类似，其中ε为所需的陷波信号。

图3 电流陷波器结构图

针对此陷波器，采用最小均方(LMS)在线调整权值，其表达式为

ω(k+1)=ω(k)+2με(k)x(k)

(11)

式中，ω(k)为神经元在第k时刻的权值；μ为学习率；ε(k)为系统输出，即陷波后的信号；x(k)为陷波器输入。

神经网络的传递函数在z域有如下的形式：

(12)

式中，ω0为频率参考值，C为cosω0的振幅。

根据上述的死区补偿方法和建立的控制器，可以搭建出如图4所示的电动汽车电驱动系统的整体控制框图。

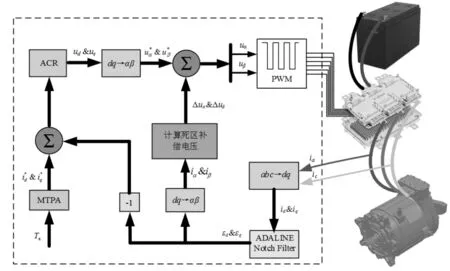
图4 基于EKF死区补偿的电驱动系统框图

3 仿真和试验

为了验证所提出算法的正确性，根据图4所示的电驱动系统框图，在Simulink环境下，建立出基于ADALINE陷波器的死区补偿控制系统模型进行仿真实验。仿真选用变步长ode23tb，起止时间为0～0.2s，电流环PI控制器的参数分别为d轴kp为1，ki为20；q轴kp为3，ki为20。d轴与q轴的陷波器参数μ分别为1×10-4和2×10-4。

IPMSM及逆变器主要参数如表3所示。其中，逆变部分为IR公司的IRFB4115PbF型MOSFET并联而成；主控MCU使用飞思卡尔MC56F84789。

表3 IPMSM及逆变器参数

3.1 Simulink仿真

首先进行输出转矩为20 Nm的实验。图5为无死区补偿时的三相电流波形，由图中可观察出，在零电流附近，由死区效应引起的电流畸变现象可以清楚地观察到。图6为使用ADALINE陷波器的死区补偿后的三相电流波形，由放大后的波形观察可知，在零电流附近，因死区效应引起的电流畸变已经被有效地抑制，且电流的扰动也较小。然后进行输出转矩为40 Nm的实验。图7为无死区补偿时的三相电流波形，由图中可观察出，在零电流附近，由死区效应引起的电流畸变现象可以清楚地观察到，且每隔60°会变得非常明显。图8为使用ADALINE陷波器的死区补偿后的三相电流波形，由放大后的波形观察可知，在零电流附近因死区效应引起的电流畸变已经被有效地抑制。

图5 20Nm时无补偿的三相电流波形

图6 20Nm时死区补偿后的三相电流波形

图7 40Nm时无补偿的三相电流波形

图8 40Nm时死区补偿后的三相电流波形

3.2 系统平台试验

搭建如图9所示的IPMSM控制系统平台。控制器参数与仿真参数一致，IPMSM与逆变器参数如表4所示。通过对实验样机进行电流波形监测及IPMSM振动测试，验证本文所提的ADALINE陷波器死区补偿算法的有效性。其中，电流数据每63 μs捕捉一次。

振动测试时，将测振仪竖直放置于电机前轴承处，测量IPMSM的径向振动。输出转矩为20 Nm时，电流波形如图10所示。图10(a)为无补偿时的电流波形，电流峰峰值为-113 A和112 A，电流畸变已用虚线框标出。图10(b)为本文提出的ADALINE陷波器死区补偿方案的电流波形，电流峰峰值为-112 A和112 A，零电流时的电流畸变现象已得到抑制。输出转矩为40 Nm时，电流波形如图11所示。图11(a)为无补偿时的电流波形，电流峰峰值为-196 A和206 A，电流畸变已用虚线框标出。图11(b)为本文提出的ADALINE陷波器死区补偿方案的电流波形，电流峰峰值为-200 A和206 A，电流畸变现象得到有效抑制。

图9 IPMSM控制系统平台基本结构

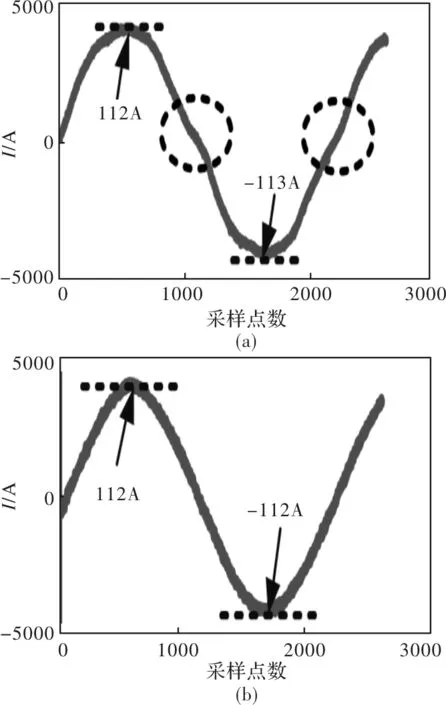
图10 20Nm电流波形

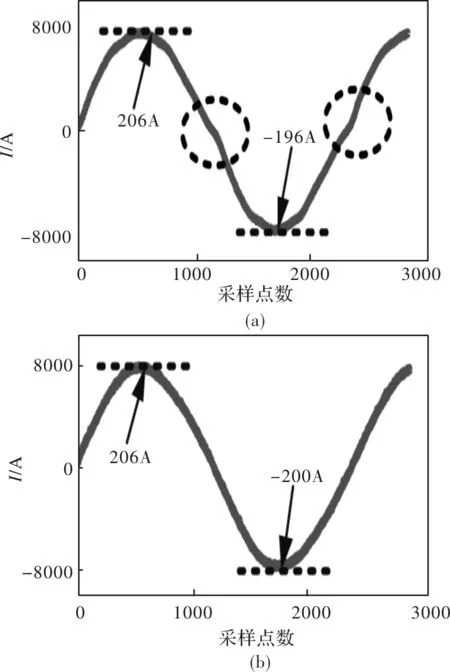
图11 40Nm电流波形

振动测试结果如表4。由表4可知，使用本文提出的ADALINE陷波器死区补偿方法较无死区补偿方法，输出转矩为20 Nm和40 Nm时，振动速度都减少100%，振动幅度分别减少92.86%和86.96%，由此可知，基于ADALINE陷波器的死区补偿方案显著地改善了IPMSM振动性能，使乘用电动车的舒适性得到提升。

表4 IPMSM振动测试结果

振动测试结果如表4所示。由表4可知，使用本文提出的ADALINE陷波器死区补偿方法较无死区补偿方法，输出转矩为20 Nm和40 Nm时，振动速度都减少100%，振动幅度分别减少92.86%和86.96%，由此可知，基于ADALINE陷波器的死区补偿方案显著地改善了IPMSM振动性能，使乘用电动车的舒适性得到提升。

4 结 语

本文分析了死区效应造成的不良影响，采用iα和iβ的线性组合判断所需补偿的电压，并使用ADALINE陷波器将直轴与交轴电流中的6次、12次谐波滤除以增强死区补偿效果。仿真与实验都表明：本文提出的基于ADALINE陷波器的死区补偿方法在不同载荷时都能有效地抑制死区效应造成的不良影响。IPMSM低速启动时的输出转矩为20 Nm和40 Nm时，其振动幅值相较于无补偿时分别减少92.86%和86.96%，使振动性能得到显著改善，进而提高整车乘坐的舒适性。