盘式永磁耦合器传动机理有限元仿真研究
王 昭,南江萍,张培培,王 菲
(西安交通工程学院 中兴通信学院,西安 710300)
0 引 言
永磁耦合器是利用机械结构实现可调传动的重要代表,在众多领域代替价格昂贵、空间占用大的变频器。由于永磁耦合器的非接触传动具有震动小、无摩擦、偏心传动、节能环保等优点[1-2],而且具有对电机过载保护及软启动等功能特点,极大程度降低因轴承的损耗导致工业过程中长时间停机或重启等风险[3-4],因此在风电、水泵、鼓风、舰船涡轮、采矿、石油等众多需要变频调速的领域得到广泛应用[5-6]。因永磁耦合器的良好特性和广泛应用,越来越多的学者对其进行理论研究[7-10],以实现更佳的传输效能和精确设计。尤其是永磁耦合器的电磁结构相对复杂,传统解析方法很难达到精细求解,因此有限元建模仿真成为重要的研究手段,相关仿真建模已经了有一定的研究[11-15]。本文依据电磁传动理论应用COMSOL软件对盘式永磁耦合器进行有限元三维瞬态建模,分析其涡流特性和电磁传动特性,并且分析几种主要参数对传动特性的影响,得出相关的规律特性。同时给出了标准的有限元建模方法,对盘式永磁耦合器的数值建模和准确设计都可以提供重要的参考。
1 有限元模型
1.1 永磁耦合器仿真模型
图1为盘式永磁耦合器的结构,由主动转子和从动转子组成,主动转子连接在电机上,从动转子连接在负载上,主动转子和从动转子无结构连接,并且之间有一定的气隙。主动转子主要由永磁铁和永磁铁托盘组成,从动转子为金属盘。相邻两个永磁铁磁极相反。
图2为盘式永磁耦合器的有限元仿真模型,仿真模型包含永磁耦合器和空间求解域,空间求解域被气隙间的旋转面分为两部分,左边为铜盘求解域,右边为磁铁求解域。
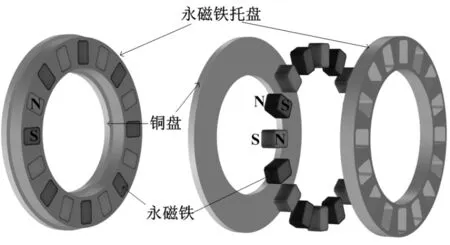
图1 盘式永磁耦合器结构

图2 盘式永磁耦合器有限元仿真模型
建模的相关计算参数如表1所示。
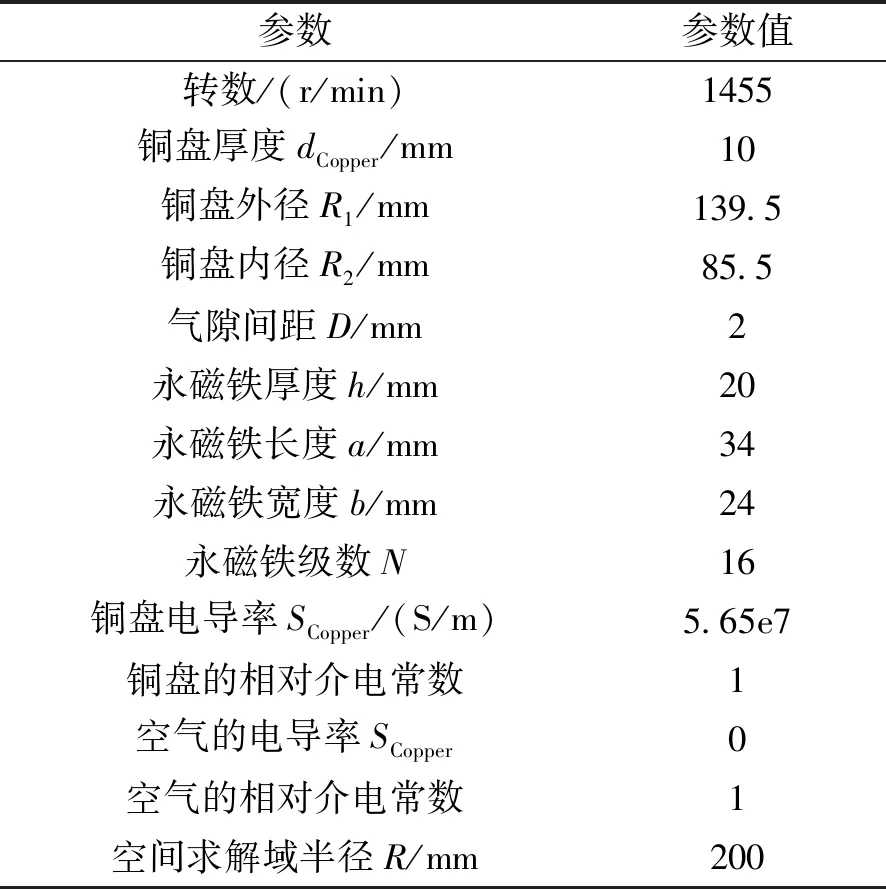
表1 仿真模型相关参数
图3为盘式永磁耦合器有限元模型的网格设计,图3(a)为耦合器结构的网格设计,图3(b)为空间求解域的网格设计。整个模型采用的基本网格单元为自由四面体,金属铜盘的网格在厚度方向共有4层,永磁铁和托盘在厚度方向共有8层网格,永磁耦合器设计的最大网格尺寸为0.25mm,求解域的最大网格尺寸为3mm。
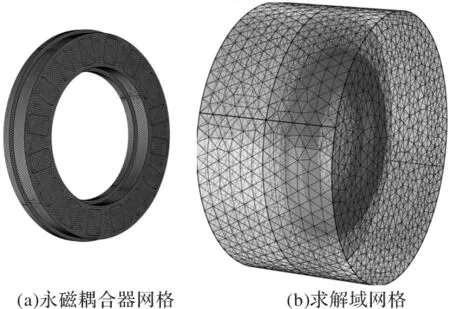
图3 有限元模型网格设计
1.2 瞬态电磁计算方程
永磁耦合器的电磁场数学模型,根据电磁学基本理论(对于低频瞬态磁场,忽略位移电流效应),永磁涡流耦合器电磁场控制方程需要应用到安培定律、磁通量守恒定律以及相应的本构关系。相关公式如下:
安培定律:
(1)
(2)
(3)
(4)
磁通量守恒:
(5)
本构关系:
(6)
(7)
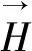
2 涡流和电磁传动特性
永磁耦合器的永磁铁提供稳定的静态磁场,当定子和转子保持相对静止时,永磁铁产生的静态磁场不会被铜盘切割,进而也不会在铜盘上产生感应,因此不会产生扭矩和轴方向的电磁力。当电机带动转子开始运动时,转子端永磁铁产生的静态磁场被铜盘切割,切割磁场会在垂直磁场的铜盘内产生环向涡流,如图4(a)所示。由于相邻永磁铁的磁极方向是相反的,因此在铜盘上产生的相邻涡流的旋转方向也是相反的,如图4(b)所示。
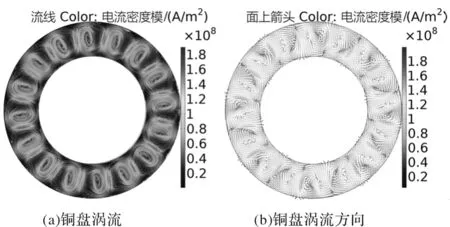
图4 涡流
永磁铁的剩余磁通(如图5(a)所示)在转子运动时使铜盘产生涡流,铜盘内形成的涡流又会产生新的磁场,其方向基本垂直于铜盘,相邻涡流产生磁场的方向也是相反的(相邻两个涡流的方向相反)。铜盘上感应产生的磁场分布与永磁铁形成的磁场分布类似,如图5(b)所示。
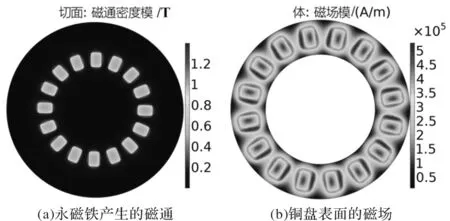
图5 磁通
以上分析可知在永磁耦合器工作时,铜盘上形成与永磁铁类似的等效磁铁,永磁铁和等效磁铁的磁极方向相反,两者产生的磁场相对,产生一定的斥力,如图6(a)所示。当转子和定子有一定的相对运动时,永磁铁和等效磁铁相互错位,产生斜向电磁力,如图6(b)所示。斜向电磁力可以分解为沿铜盘切线方向和轴向方向的分力,切向受力形成扭矩,当转子转动时,扭矩带动定子旋转,同时在轴方向产生一定的排斥力。

图6 电磁场特性
图7(a)为铜盘1/4空间内4个切向力监测点标记图,图7(b)为4个监测点的切向受力,图7(c)和图7(d)为轴向力和扭矩。可以看出切向受力的包络特性和扭矩曲线特性基本一致,那是因为永磁铁的扭矩是由铜盘所有区域切向力积分所得。从图7还可以看出无论是扭矩还是轴向力在转子起动时,其电磁力都是在一定时间范围内产生正弦震荡,最终趋于稳定。因此永磁耦合器的起动是软起动,较好的保护电机。
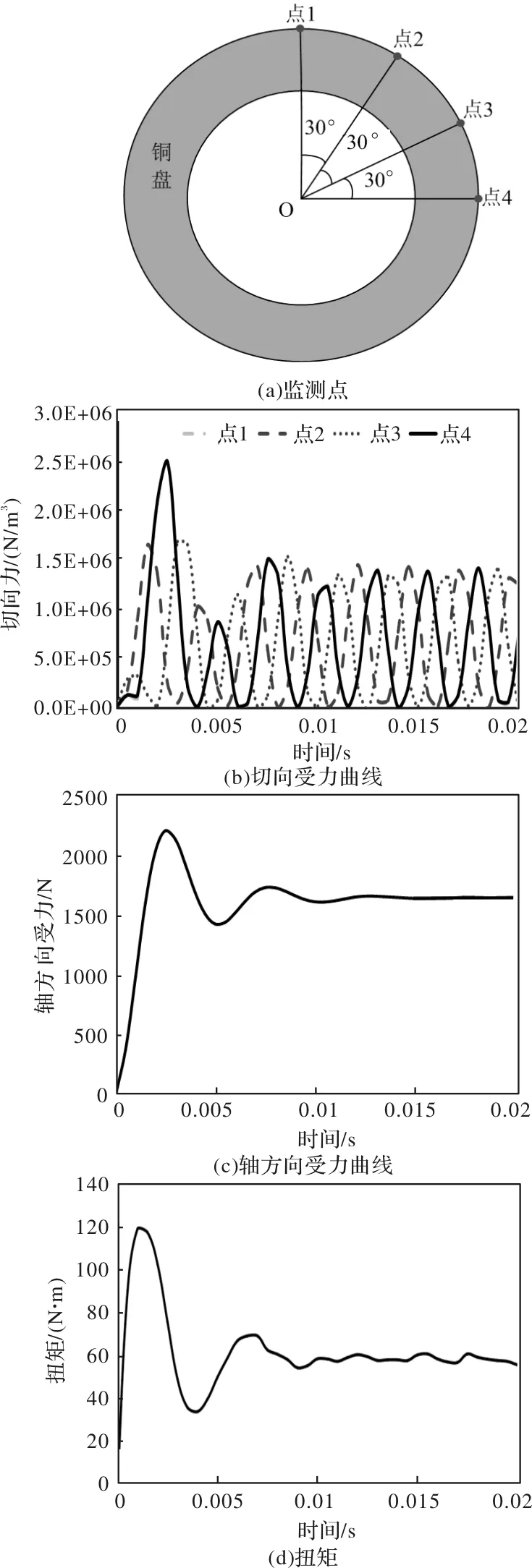
图7 永磁耦合器受力情况和扭矩曲线特性
3 参数对传动的影响
从以上的涡流特性和电磁传动特性可以看出,影响其电磁力的因素较多,在导体盘一定情况下,主要的影响因素有磁铁的材质、磁铁的级数和气隙大小。文中对着3种因素进行了详细的分析。
3.1 永磁铁规格
常用永磁铁又叫钕铁硼磁铁,工艺、原料配比和磁化等因素导致其规格不同,不同规格尺寸的永磁铁的剩余磁通有所不同。本文分析牌号为N38SH、N42SH、N45SH的3种永磁铁,其磁铁的剩余磁通强度分别为1.22T、1.25T、1.29T,其它参数不变如表1所示。
从图8(a)可以看出剩余磁通强度的变化,并不影响扭矩的曲线特性,还是原有的正弦振荡特性,周期不变,只是导致其幅值有所变化,永磁铁的剩余磁通强度越大,其产生的扭矩越大。其平稳扭矩和剩余磁通的关系绘制成曲线如图8(b)所示,可以看出其扭矩与剩余磁通强度基本呈绝对线性关系,剩余磁通越大,平稳扭矩越大。
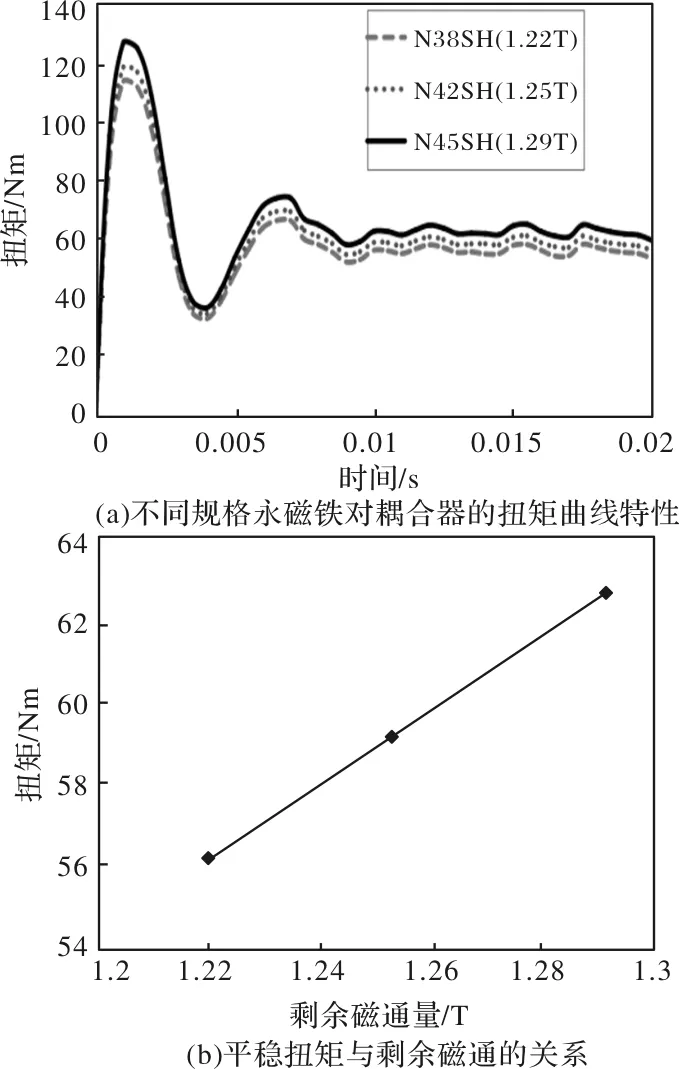
图8 永磁铁规格对受力的影响
3.2 永磁铁级数
永磁耦合器相邻两个永磁铁的磁极相反,因此永磁铁的级数只能为偶数,本文取永磁铁的级数为12、14、16、18、20、22、24、26(26为此规模永磁耦合器最多可安装的磁铁数量)进行计算分析,其它参数不变如表1所示。
图9为磁极数量对扭矩的影响,从图9(a)和图9(b)可以看出磁极数量在一定数量内(N=12~24)的变化对耦合器产生扭矩在整体规律上变化不大,但是当磁极数量较多(N=26)导致相邻磁极间距较小时,震荡波形会产生异常,甚至扭矩出现负值。同时可以看出震荡周期(N=12~24)与磁极的数量有关系,磁极数量越少需要平稳的周期越长,也就是说磁极数量越多,永磁耦合器产生的扭矩越快稳定。
图9(c)为平稳扭矩和磁极数量的关系绘制成曲线,可以看出磁极数量少于24时,磁极数量越多,永磁耦合器产生的平稳扭矩越大,当磁极数量大于24时永磁耦合器产生的平稳扭矩基本不再变大。说明磁极数量过多导致在铜盘上产生的单元涡流相互影响,反而影响永磁耦合器的传输效率。
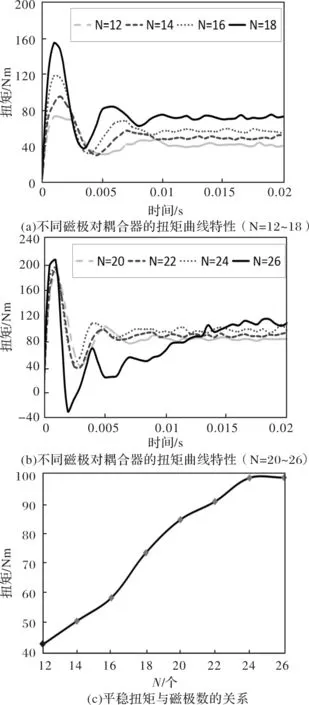
图9 磁极对受力的影响
3.3 气隙间距
永磁耦合器通过气隙的调整,对负载进行调速。本文取1mm、2mm、4mm、8mm和15mm的气隙间距进行计算分析,其它参数不变如表1所示。
图10为气隙间距对扭矩的影响,从图10(a)可以看出气隙间距的变化对耦合器产生扭矩的震荡周期不产生影响,只改变其整体幅值,其平稳周期也与气隙间距没有关系。还可以看出气隙间距越大,永磁耦合器产生的扭矩越小。其平稳扭矩和气隙间距的关系绘制成曲线,如图10(b)所示,可以看出其扭矩与气隙间距呈指数态递减关系(对数上呈线性关系),气隙间距越大,平稳扭矩越小。

图10 气隙间距对受力的影响
4 结 论
对盘式永磁耦合器进行标准有限元建模,分析其机理。永磁耦合器工作时,永磁铁的剩余磁通通过空间耦合使铜盘上产生涡流(相邻涡流方向相反),铜盘感应产生的磁场与永磁铁形成的磁场方向相反,永磁铁在相对偏移时使铜盘产生扭矩和轴向力。在铜盘不变的情况下,扭矩和轴向力与永磁铁的规格、永磁铁的级数和气隙间距相关。永磁铁的剩余磁通强度越大或磁极数量越多都会使其扭矩和轴向力线性增大;永磁铁和铜盘之间的气隙增大,会导致扭矩呈指数态递减。

