准线之“准”有深意
吴江盛泽中学 孙四周
问:“圆心是圆的一部分吗?”
答:“不,圆心不是圆的一部分.”
问:“准线是抛物线的一部分吗?”
答:“不,准线不是抛物线的一部分.”
虽然圆心是圆所固有的要素,但是它不能算是圆上的点,因为它不符合圆的定义,圆心到它自身的距离不等于半径长(它等于0).
类似地,抛物线的准线是其固有的一个要素.抛物线是用准线和焦点来定义的,可以说它一刻也离不开准线和焦点,但准线(以及焦点)不算是抛物线的一部分.
那么准线“有实际意义”吗?
一、抛物线与“抛物”的关系
画出一条抛物线比画出一个圆容易得多.捡起一块小石头斜向上抛出,它在空中翩然飞过又在不远处回归地面,这条美丽的弧线就是抛物线.这个做法非常简单,这个说法非常直接,数学上为什么不用它来做抛物线的定义(即“斜抛物体所形成的轨迹叫做抛物线”)呢?因为这里要用到“斜”“抛”“物体”“(运动)轨迹”等字眼,而物体在运动过程中还要考虑地球的引力、空气阻力以及初速度大小等等,初速度过小和过大都不能形成抛物线(过小是椭圆,过大是双曲线).数学需要抽象化,就像物理上抽象出“理想气体”“理想弹簧”“理想真空”“理想电阻”一样.“理想的斜抛运动”中,地球是无限大的(物体所受引力平行向下)、空气是不存在的(没有阻力),这在自然界中根本不可能存在,而其表述反而不如“平面内到定点F和定直线l(F∉l)距离相等的点的集合”更容易、更明确,所以数学上的定义采用了后者.
斜抛物体的轨迹“真的”是抛物线吗?
设以仰角α,速率v0斜向上抛出一个物体,则该运动可以分解为两个运动,一是竖直方向的匀减速运动,二是水平方向的匀速直线运动(竖直方向受地球引力,水平方向不受力).建立坐标系如图1,设在t时刻物体的坐标为P(x,y),则
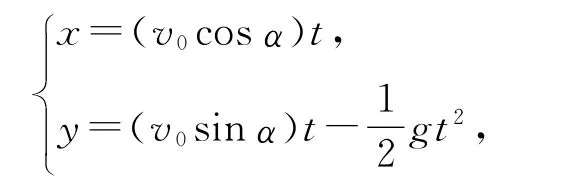
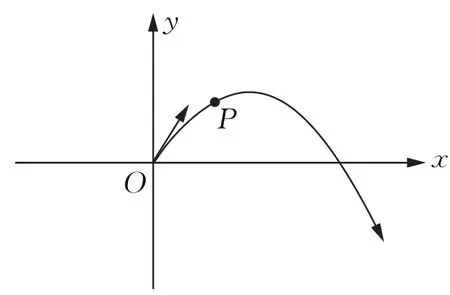
图1
这是一个参数方程,消去参数t即得物体运动的轨迹方程为:
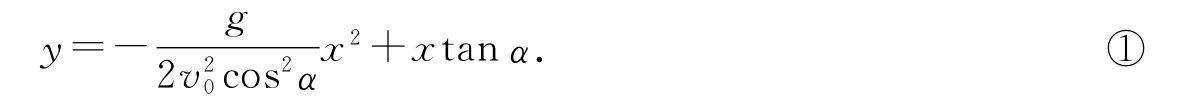
这是一个二次函数,其图象我们称之为抛物线.
这里所说的“抛物线”是实际斜抛物体的轨迹吗?可以说是的.只不过我们忽略了空气阻力,而且认为地球引力始终是向下的(也就是把地球想象成无穷大,地面是无限的水平平面),这就是高中教材的处理方法.
它与解析几何上所说的抛物线是同一个概念吗?是的.只要我们重新建立一个坐标系,把坐标原点选在抛物线的顶点,一条坐标轴是抛物线的对称轴所在的直线,就可以得到解析几何上的“抛物线”标准方程.所有二次函数均可如此处理,因此二次函数的图象与解析几何中的抛物线确实是等价的.
二、抛物线准线的实际意义
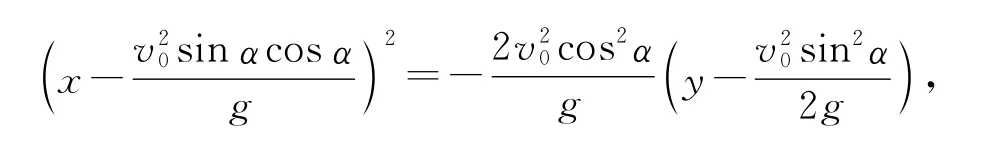
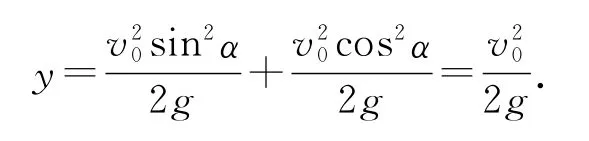
注意,这里不含有倾斜角α,只含有初速度v0(g是常数),是不是很神奇?抛物线的准线与斜抛的角度无关,只与初速度有关.也就是说,初速度相同的一系列的抛物线,其最大高度以及水平跨度互不相同,但是它们有共同的准线(图2),这是我们当初所没有想到的.
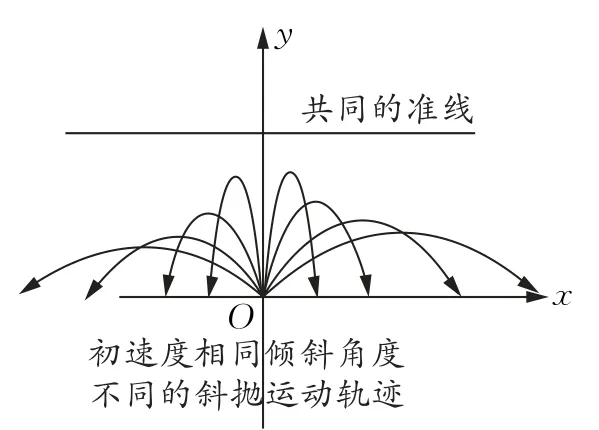
图2
三、特别的爱给特别的你
①中α≠90°,当α=90°时,正好是竖直上抛运动,此时有:

此式不是关于x的二次函数,此过程中物体一直在y轴上,先上后下,轨迹是折线而不是抛物线.方程②描述的,是该物体的高度随时间而变化的规律,由此很自然地想到计算它的最大高度.根据二次函数最大值公式,
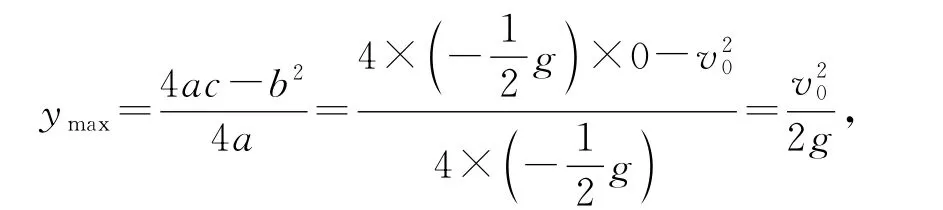
也就是说,如果以初速度v0把物体竖直上抛,它所能达到的最大高度恰好是准线所在的位置.这就揭示了一个永恒的、也是冷酷的自然规律:调整斜抛的方向,固然可以使物体达到不同的高度,然而大自然为你设立了一个天花板,你永远突破不了.但是大自然同时给了我们希望,那就是:要想达到更大的高度,只要增加初速度就行了.有在,没有什么不可以!这就是抛物线准线的实际意义,它在限制我们的同时也给我们无尽的自由!椭圆和双曲线的准线,是否也有其特别的实际意义呢?应该有吧.用《诗经》中的一段结束本文:“蒹葭苍苍,白露为霜.所谓伊人,在水一方.溯洄从之,道阻且长.溯游从之,宛在水中央.”

