分析结构，联想通法

南京市大厂高级中学 余建国

基本不等式的应用是高考的“必考点”．由于不断地改编和创新，这类问题看上去越来越复杂，但条件和目标的本质结构没有变化．本文通过一个问题的多角度求解，帮助同学们从结构的角度寻找解题的入口，掌握这类问题本质和求解的通法．

若干高考试题或模拟试题的“创作”思路都是源于下列问题：

题根已知x＞0，y＞0，x+y=1，求的最小值．

这道题是一个“题根”，对应的“乘1法”是众多方法中用起来比较利索的方法，只要条件和目标的结构符合这样的要求，就可以“套用”，系数不为1也是如此．

例已知正数x，y满足的最小值为_______．

分析一注意到互为倒数关系，凑一凑的倒数以及它们的关系，将条件向目标方向配凑．

解法一由题意得

分析二反过来想，将目标向条件看齐，对这种形式分离常数，出现后，对化整式后因式分解，形成基本模式．

解法二由题设可得（x-1）（y-1）=1．

分析三由，得这样目标就可以简化为4y+9x了，故问题转化为：已知正数x，y满足，则4y+9x的最小值为______．利用条件对目标变形，转化到最原始、最基本的题型上来了．由此可见，解题时不能隔离条件和目标，“用联系的观点看问题”是一种哲学高度．

分析四对照题根，令则已知条件为a+b=1，目标问题转化为：已知正数a，b满足a+b=1，则的最小值为_______．试试换元！通过换元，可以化陌生为熟悉．换个角度说，命题老师就是在题根的基础上将字母换复杂而已．另外，对照分析三，可知分析四与分析三的结构是一样的．

分析五由于，所以y可以用x表示，即将目标消去y，化为关于x的一元函数求解，这种方法体现了函数思想，是以不变应万变的通法．

解法五由已知得

分析六除基本不等式外，如果我们掌握更多的重要不等式，如柯西不等式，那么解决这类问题时渠道就更多，过程更简单明了．如解法一用柯西不等式证明为：

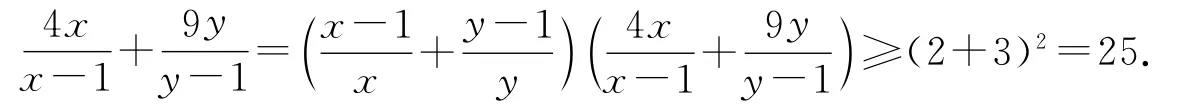
又如：已知a，b是正数，x，y是任意实数，则当且仅当时取“=”．其证明：左边-右边=注意到它的结构，利用这个结论，可有如下解法．

解法六令则a+b=1，

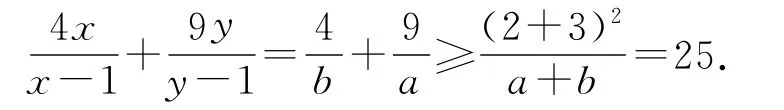
这是将分析四证了，但不是题根中的“乘1法”．类似地，如解法七．

解法七因为

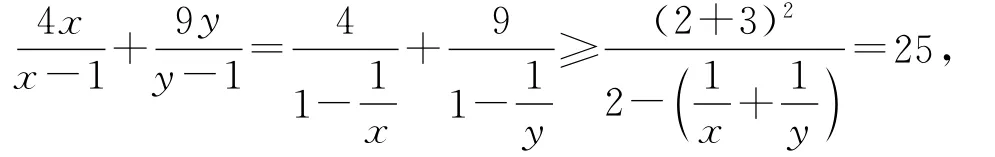
总之，基本不等式结构简单，均匀对称，两个正数通过加法、乘法、除法和开方四种运算，产生了它们算术平均数与几何平均数的内在规律．这种内在规律有严谨的结构，解题的入口就是分析结构，对条件、目标作适当变形、换元和转化．