从连分数到黄金分割

韦 磊

上一期，我们看到了连分数在历法中的应用，本期我们来看看连分数与黄金分割的渊源．

连分数与黄金分割

先看方程x2=ax+1，a＞0，可以将其写成：

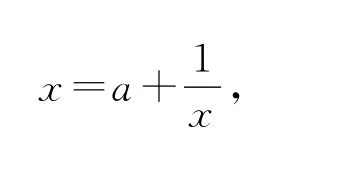
接下来是见证奇迹的时刻，继续把右边式子中的x换成得到：

继续迭代，就会得到连分数：

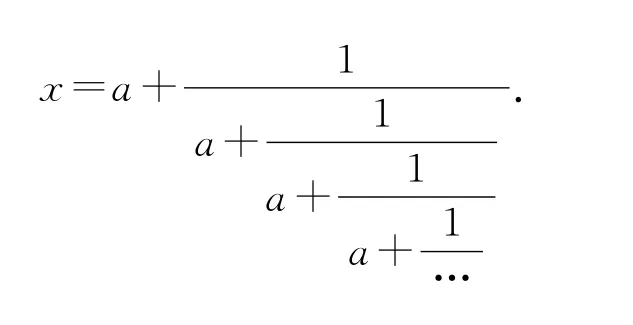
当然要说一下，只能将方程x2=ax+1，a＞0的正根进行如此改写，这样写出来的“无限连分数”才有意义，在这里大家只做一个直觉上的认识：这个无限连分数显然只能是正数，因此只能代表正根．

比如说取a=1，得到方程x2=ax+1的正根为根据上面的连分数写法，就可以得到：

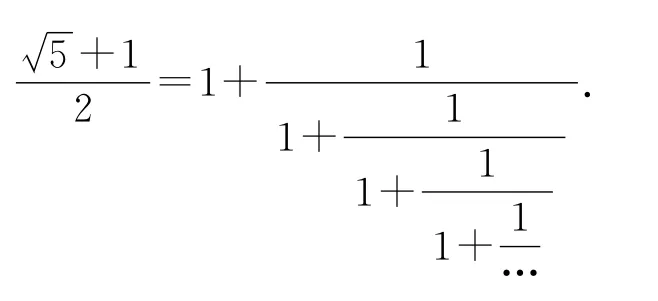
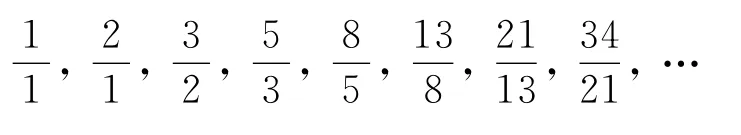
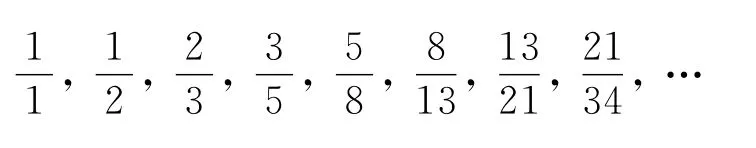
这让我们想起了著名的斐波那契数列：1，1，2，3，5，8，13，21，34，55，89，…

该数列从第三项开始，每一项就是前两项之和，相信大家已经见过．

如果真是如此，那反过来不就是说明，斐波那契数列的前一项与后一项的比值，越来越趋近于黄金分割比？

说到黄金分割，那就不得不提2019年的一道高考题：

（2019全国Ⅰ卷）古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是0．618，称为黄金分割比例），著名的“断臂维纳斯”便是如此．此外，最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是若某人满足上述两个黄金分割比例，且腿长为105cm，头顶至脖子下端的长度为26cm，则其身高可能是（ ）

A.165cm B.175cm

C.185cm D.190cm

【解法提示】这道题的解题要点，除了正确理解题意以外，那便是“可能”二字，也就是说，得到的结果就不可能是精确值．题目给出的条件也没有精确的：肚脐近似当做腿部上端，咽喉近似当做脖子下端．为方便，画出一个示意图：

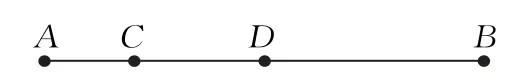
图1

图中A点代表头顶，C点代表咽喉，D点代表肚脐，B点代表脚底．根据题意：AC=26，，实际上就有两种算法了．这道题的难点，也就是计算．这道题的背景，也就在计算上．

前面提到了黄金分割比与斐波那契数列的关系：斐波那契数列的前一项与后一项的比值就越来越趋近于．换句话说，这些比值有时候可以近似代替黄金分割比．适当挑选比值，可以化简本题中的计算．

我们看看斐波那契数列：1，1，2，3，5，8，13，21，34，55，……发现其中的13似乎与题目中的26有约分的关系，而21和105也有这种关系，于是我们如果我们利用，就利用来代替0．618：

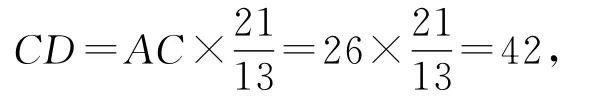
算出来身高就是26+42+105=173，和B选项最接近．如此计算量就大大减少了．

通过此题，大家应该能够感受到，适当应用连分数对无理数的近似表示，在实际计算中的作用．事实上，不仅黄金分割比的近似值有作用，黄金分割比在一些近似计算中也具有相当大的作用．

黄金分割比的定义和再生性

图2

我们很容易知道，一条线段有两个黄金分割点，左右各一个：

图3

而且两个黄金分割点关于AB的中点对称．题目向我们展示了黄金分割比的悠久历史，同时也展示了其美学意义．不过，相比“美学”这种主观性特别强的感受来说，黄金分割比的另一性质使得它在实际应用中，发挥出了非常重要的作用，这便是——黄金分割的再生性．

如图3，C，D都是AB的黄金分割点，则C也是线段AD的黄金分割点，当然D也是线段CB的黄金分割点．

这就是黄金分割比的再生性——当找到了AB的黄金分割点D以后，那么AD的黄金分割点就不用找了！同时若考虑到应用场景是实际应用，C和D关于AB的中点对称，则凭着人工就能实现如下自动化操作：

首先找到AB的一个黄金分割点C；

将线段AB对折，使得A，B重合，则与C重合的点就是AB的另一个黄金分割点D；

将AD对折，与C重合的点就是AD的另一个黄金分割点E；

将AC对折，与E重合的点就是AC的另一个黄金分割点F……

如此循环，只需要一开始计算一次点C，其余的基本上可以自动进行．

可别小看这种看起来堪比游戏的操作，在20世纪，数学家华罗庚就是据此发明了“优选法”，产生了深远的影响．