求数列通项的一般方法

南京市教学研究室 龙艳文

求数列通项是数列这一章的重点问题之一．我们通过以题组形式对问题进行归类研究，分析递推关系的结构特征，提炼出有章可循的解题方法，从而构建数列中有关最值、单调性和不等式恒成立问题的解题思维模式结构图．

一、解题思维模式形成

题组一：叠加（乘）法

例1（1）已知a1=1，an+1=an+2n，n∈N*．求数列｛an｝的通项公式an．

解n≥2时，

an=a1+（a2-a1）+（a3-a2）+…+（an-an-1）=1+21+…+2n-1=2n-1，

当n=1时，21-1=1=a1，上式也成立．

所以an=2n-1，n∈N*．

（2）已知a1=1，an+1=2nan，n∈N*．求数列｛an｝的通项公式an．

解n≥2时

当n=1时，20=1=a，上式也成立．

方法小结

（1）形如an-an-1=f（n）（n∈N且n≥2）的递推关系，用叠加法，即当n∈N，n≥2时，

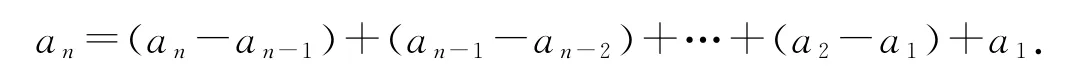
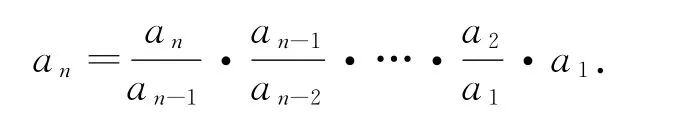
题组二：进（退）项作差（和、商、积）

例1（1）设数列｛an｝的前n项和为Sn，已知a1=1，a2=2，且an+1=3Sn-1-Sn+3（n∈N*，n≥2），证明：an+2=3an．

解因为对任意n∈N*，n≥2，有an+1=3Sn-1-Sn+3，①

所以n≥1时有，an+2=3Sn-Sn+1+3，②

由②-①，得an+2-an+1=3an-an+1，即an+2=3an（n≥2，n∈N*）．又a1=1，a2=2，所以a3=3S1-S2+3=3a1-（a1+a2）+3=3=3a1，所以任意n∈N*，an+2=3an．

（2）设数列｛an｝的各项都是正数，对任意n∈N*，都有a31+a32+a33+…+a3n=S2n+2Sn，其中Sn为数列｛an｝的前n项和．

（i）求a1，a2；（ii）求数列｛an｝的通项公式．

解（i）令n=1，则a31=S21+2S1，即a31=a21+2a1，解得a1=2或a1=-1或a1=0．

又因为数列｛an｝的各项都是正数，所以a1=2．

令n=2，则a31+a32=S22+2S2，即a31+a32=（a1+a2）2+2（a1+a2），

将a1=2代入得a32-a22-6a2=0，解得a2=3或a2=-2或a2=0．

又因为数列｛an｝的各项都是正数，所以a2=3．

（ii）因为a31+a32+a33+…+a3n=S2n+2Sn，①

所以a31+a32+a33+…+a3n-1=S2n-1+2Sn-1（n≥2），②

由①-②，得a3n=（S2n+2Sn）-（S2n-1+2Sn-1）=（Sn-Sn-1）（Sn+Sn-1+2）=an

（Sn+Sn-1+2）．

因为an＞0，所以a2n=Sn+Sn-1+2，③

所以a2n-1=Sn-1+Sn-2+2（n≥3），④

由③-④，得a2n-a2n-1=an+an-1，即an-an-1=1（n≥3）．

又a2-a1=1，所以an-an-1=1（n≥2），

所以数列｛an｝是一个以2为首项，1为公差的等差数列，

所以an=a1+（n-1）d=n+1．

方法小结

对数列递推公式进（退）项相减．

例2（1）已知数列｛an｝满足an=an-1-an-2（n≥3，n∈N*），它的前n项和为Sn．若S9=6，S10=5，则a1的值为_______．

解由an=an-1-an-2（n≥3），得an+1=an-an-1（n≥2），

两式相加得an+1=-an-2（n≥3，n∈N*），从而an+3=-an（n∈N*），

可得an+6=an（n∈N*）．

由S9=6，S10=5，得a10=-1．

因为a10=a4=-a1，所以a1=1．

（2）已知数列｛an｝的前n项和为Sn，且对任意正整数n都有求数列｛an｝的通项公式．

解由，得

①+②得an+an+1=（-1）n（-an+1）+

当n为奇数时，，所以

当n为偶数时

方法小结

对数列递推公式进（退）项相加．

例3（1）已知数列｛an｝的各项均不为零，且满足a1a2a3…an=an+1，n∈N*，a1=2，求an．

解n=1时，a2=a1=2．

因为a1a2a3…an=an+1，n≥1，①

所以a1a2a3…an-1=an，n≥2，②

由①÷②，得an+1=a2n，n≥2，所以an＞0，则lnan+1=2lnan，n≥2，

所以lnan=2n-2lna2=ln22n-2，n≥2，所以an=22n-2，n≥2．

（2）已知数列｛an｝各项均为正数，且对任意n∈N*，都有．求证：数列｛an｝为等比数列．

证明因为

所以a2n+2=an+1an+3，n=2时，a1a3=a22，故a2n+1=anan+2，n∈N*，

因此，数列｛an｝为等比数列．

方法小结

对数列递推公式进（退）项相除．

题组三：配凑构造新数列

例1（1）已知数列｛an｝满足a1=1，an+1=a2n+2an，n∈N*．求数列｛an｝的通项公式an．

解因为an+1=a2n+2an，所以an+1+1=（an+1）2．

因为a1+1=2＞0，所以a2+1＞0，…，an+1＞0，…，

所以ln（an+1+1）=2ln（an+1），故｛ln（an+1）｝是首项为ln2，公比为2的等比数列．

所以ln（an+1）=2n-1ln2，所以an+1=22n-1，

所以an=22n-1-1，n∈N*．

（2）已知数列｛an｝满足a1=1，nan+1=（n+2）an+2n（n+1）（n+2），n∈N*，求数列｛an｝通项公式an．

解因为nan+1=（n+2）an+2n（n+1）（n+2），

方法小结

通过变形、化简、换元等，构造一个新的数列使之成为一个等差（比）数列．

例2已知数列｛an｝的各项都为正数，且对任意n∈N*，a2n+1=anan+2+k（k为常数）．已知a1=a，a2=b（a，b为常数），是否存在常数λ，使得an+an+2=λan+1对任意n∈N*都成立？若存在，求出λ；若不存在，说明理由．

解存在常数，使an+an+2=λan+1．证明如下：

因为a2n+1=anan+2+k，所以a2n=an-1an+1+k，n≥2，n∈N*．

所以a2n+1-a2n=anan+2-an-1an+1，

即a2n+1+an-1an+1=anan+2+a2n．

由于an＞0，此等式两边同除以anan+1，

即当n∈N*，都有

因为a1=a，a2=b，a2n+1=anan+2+k，所以

所以对任意n∈N*，都有an+an+2=λan+1，此时

方法小结

通过变形、化简、换元等，构造一个新的数列使之成为常数列．

例3已知数列｛an｝中，a1=1，设求数列｛bn｝的通项公式．

解由得因为所以化简得bn+1=4bn+2，即，且所以是首项为，公比为4的等比数列．

方法小结

通过变形、化简、换元等，构造一个新的数列使之成为常见递推形式．

题组四：消去法

例1对于给定的正整数k，若数列｛an｝满足an-k+an-k+1+…+an-1+an+1+…+an+k-1+an+k=2kan对任意正整数n（n＞k）总成立，则称数列｛an｝是“P（k）数列”．若数列｛an｝既是“P（2）数列”，又是“P（3）数列”．证明：｛an｝是等差数列．

证明因为｛an｝是“P（2）数列”，所以：

n≥3时，an-2+an-1+an+1+an+2=4an，

又因为｛an｝是“P（3）数列”，所以：

n≥4时，an-3+an-2+an-1+an+1+an+2+an+3=6an．①

（要证｛an｝是等差数列，就是要证明an-1+an+1=2an，即要消去an-3，an-2，an+2，an+3）

n≥4时，an-3+an-2+an+an+1=4an-1，②an-1+an+an+2+an+3=4an+1，③

②+③-①得：2an=4an-1+4an+1-6an，

所以2an=an-1+an+1

所以an+1-an=an-an-1，

所以数列｛an｝是从第3项起为等差数列，设其公差为d，则

｛an｝：a1，a2，a3，a3+d，a3+2d，…，

所以数列｛an｝是等差数列．

方法小结

对于单数列多递推关系，通过进（退）项，构造方程组，消去两端项．

例2在正项数列｛an｝和｛bn｝中，a1=2，b1=4，且对任意的n∈N*，且an，bn，an+1成等差数列，bn，an+1，bn+1成等比数列．求数列｛an｝，｛bn｝的通项公式．

解因为an，bn，an+1成等差数列，bn，an+1，bn+1成等比数列，

所以2bn=an+an+1，a2n+1=bnbn+1．

因为｛an｝是正项数列，所以

所以n≥2时

因为a1=2，b1=4，a2=6，b2=9，所以

所以对任意的n∈N*，，所以bn=（n+1）2．

当n≥2时，，对n=1也成立，

所以an=n（n+1）．

方法小结

对于双数列交错递推关系，消去其中一个数列形式，转化为单数列的递推关系．

例3 已知数列｛an｝中，a1=1，数列｛bn｝中，b1=0．当n≥2时，，求an，bn．

解因为当n≥2时

所以｛an+bn｝为常数列，即an+bn=a1+b1=1，①

所以｛an-bn｝是首项为1，公比为的等比数列，

方法小结

对于双数列交错递推关系，由双数列合并形式构造成基本数列递推关系，再求合并形式的通项，最后分别求两个数列的通项．

题组五：归纳猜想

例1设数列｛an｝满足a1=3，则a100=_______．

解析

方法小结

归纳猜想数列的通项形式，再证明．

二、解题思维模式构建

以上五个题组的解题思维过程可以归纳为如下的模式图：

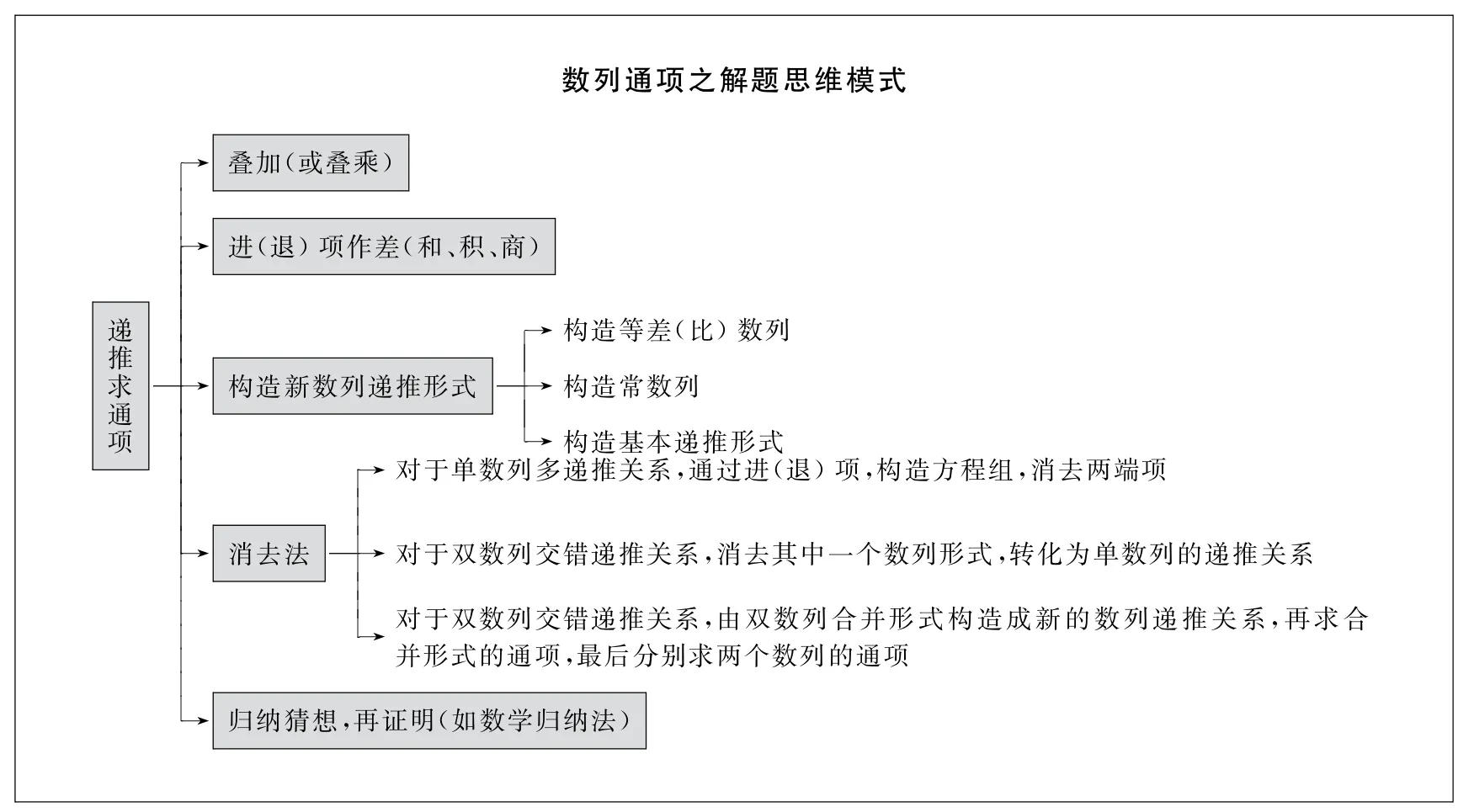
同学们在求解数列通项问题时，按照图中的步骤分析求解，一定可以事半功倍．